Теоретичні відомості

Запишемо систему n лінійних алгебраїчних рівнянь з n невідомими:

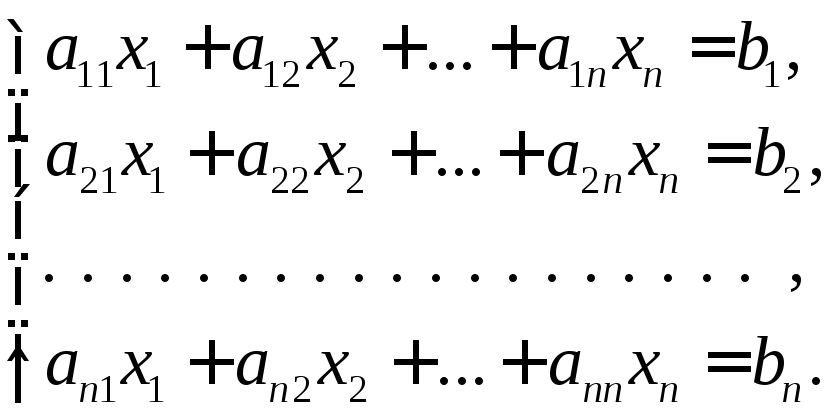(1)

Сукупність коефіцієнтів цієї системи запишемо у вигляді таблиці:

(2)

Використовуючи поняття матриці, систему рівнянь (1) можна записати в матричному вигляді:

АХ=В,

де Х та В – вектор-стовпчик невідомих та вектор-стовпчик правих частин відповідно:

, .

Необхідною та достатньою умовою існування єдиного розв’язку системи лінійних алгебраїчних рівнянь (1) є умова . У випадку рівності нулеві визначника матриця називаєтьсявиродженою. При цьому система лінійних алгебраїчних рівнянь або не має розв’язку, або має безліч розв’язків.

Метод простої ітерації

Одним з найпростіших ітераційних методів розв’язання систем лінійних алгебраїчних рівнянь є метод простої ітерації – метод послідовних наближень. Проілюструємо цей метод на прикладі розв’язання системи лінійних алгебраїчних рівнянь 3-го порядку:

за умови, що її матриця А=[a_ij] є не виродженою.

Перепишемо систему у вигляді:

(3)

Чи в матричній формі:

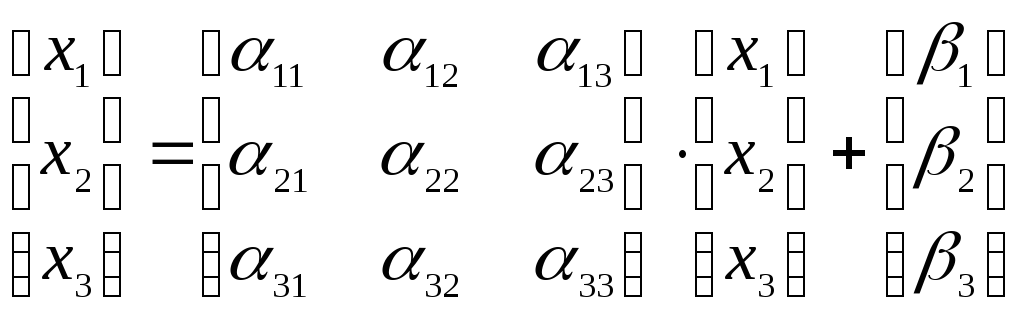
або

.

Задамо деякі початкові (нульові) наближення значень невідомих: _{, ,} . Нульове наближення може бути взяте довільно, наприклад, стовпчик вільних членів.

Підставимо ці значення в праві частини рівнянь системи (3) й отримаємо для ,,новіперші наближення:

.

Аналогічно, підставляючи в систему (3) значення перших наближень, отримаємо другі наближення:

й т. д.

Ітераційний процес продовжується до тих пір, поки значення ,,не стануть близькими із заданою точністюдо значень,,відповідно. Т. б., критерієм закінчення ітераційного процесу є виконання умови:

Для збіжності ітераційного процесу достатньо, щоб норма матриці А, яка складається з коефіцієнтів при невідомих у правих частинах рівнянь системи (3), була менша 1:

.

Метод Гауса

Метод Гауса розв’язання систем лінійних алгебраїчних рівнянь – це метод послідовного виключення невідомих. Він заснований на приведенні матриці (2) до трикутного вигляду.

Спочатку за допомогою першого рівняння виключається з усіх наступних рівнянь системи. Потім за допомогою другого рівняння виключаєтьсяз третього та всіх наступних рівнянь. Цей процес, який називаютьпрямим ходом методу Гауса, продовжується до тих пір, поки у лівій частині останнього (n-го) рівняння не залишиться лише один член з невідомим , тобто матриця (2) системи буде приведена до трикутного вигляду.

Зворотний хід методу Гауса полягає в послідовному обчисленні шуканих невідомих: розв’язуючи останнє рівняння, знаходимо єдине у цьому рівнянні невідоме . Далі, використовуючи це значення, з попереднього рівняння обчислюємой т. д. Останнім знаходимоз першого рівняння.

Таким чином, процес розв’язання системи (1) за методом Гауса розпадається на два етапи.

Проілюструємо цей метод на прикладі розв’язання системи лінійних алгебраїчних рівнянь 3-го порядку:

(4)

за умови, що її матриця А=[a_ij] є не виродженою.

Вважатимемо, що . Для виключенняз другого рівняння додамо до нього перше, помножене на. Помноживши перше рівняння наі додавши результат до третього рівняння, також виключимо з нього. Отримуємо рівносильну (4) систему рівнянь виду:

(5)

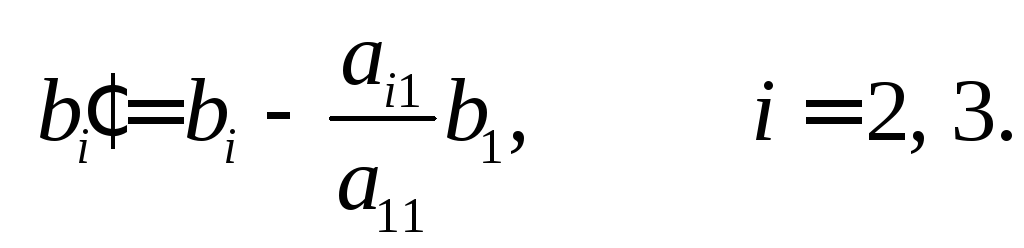
Тепер із третього рівняння системи (5) потрібно виключити . Для цього помножимо друге рівняння наі додамо результат до третього. Одержимо:

(6)

Матриця системи (6) має трикутний вигляд. На цьому закінчується прямий хід методу Гауса.

Зворотній хід починається з розв’язання третього рівняння системи (6):

Використовуючи це значення, можна знайти із другого рівняння, а потіміз першого:

Аналогічно будується обчислювальний алгоритм для лінійної системи з довільною кількістю рівнянь.