
4. Алгебраїчні структури
Приклади розв’язання типових задач
Задача
1.
З’ясувати,
чи є алгебраїчними операціями додавання
та скалярний добуток двох векторів,
заданих на множині
![]() векторів площини.
векторів площини.
Розв’язання.
Додавання
двох векторів площини є бінарною
операцією, оскільки для довільних
векторів
![]() можна однозначно побудувати вектор
можна однозначно побудувати вектор![]() .
Скалярний добуток двох векторів площини
не є бінарною операцією в множині
.
Скалярний добуток двох векторів площини
не є бінарною операцією в множині![]() ,
бо скалярний добуток є число, а не вектор,
і, отже, не є елементом множини
,
бо скалярний добуток є число, а не вектор,
і, отже, не є елементом множини![]() .
.
Задача
2.
З’ясувати,
чи буде алгебраїчною операцією знаходження
спільного дільника натуральних чисел
![]() і
і![]() в множині
в множині
![]() .
.
Розв’язання.
Для
будь-яких натуральних чисел можна знайти
їх спільний дільник, але результат цієї
дії може бути неоднозначним: числа
![]() і
і![]() можуть мати кілька спільних дільників.
Отже, знаходження спільного дільника
двох натуральних чисел не є алгебраїчною
операцією.
можуть мати кілька спільних дільників.
Отже, знаходження спільного дільника
двох натуральних чисел не є алгебраїчною
операцією.
Задача
3.
З’ясувати,
чи будуть алгебрами структури:
a)
![]() ;
b)
;
b)
![]() .
Знайти підалгебри.
.
Знайти підалгебри.
Розв’язання.
Структура
![]() є алгеброю, оскільки множення є
алгебраїчною операцією на множині
є алгеброю, оскільки множення є
алгебраїчною операцією на множині
![]() :
:
![]()
![]() .
Підалгеброю
буде структура
.
Підалгеброю
буде структура
![]() ,
оскільки
,
оскільки
![]() і множина
і множина
![]() є
замкненою відносно операції множення.
є
замкненою відносно операції множення.
Структура
![]() не є алгеброю, оскільки додавання не є
алгебраїчною операцією на множині
не є алгеброю, оскільки додавання не є
алгебраїчною операцією на множині
![]() :
:
![]() .
.
Задача
4.
Нехай
задано алгебру
![]() ,
носієм якої є множина додатніх дійсних
чисел
,
носієм якої є множина додатніх дійсних
чисел
![]() ,
з бінарною операцією множення, унарною
операцією знаходження оберненого
елемента і нульарною операцією 1
та алгебру того ж типу
,
з бінарною операцією множення, унарною
операцією знаходження оберненого
елемента і нульарною операцією 1
та алгебру того ж типу
![]() .
Довести, що відображення
.
Довести, що відображення
![]() є ізоморфізмом.
є ізоморфізмом.
Розв’язання.
Доведемо,
що відображення
![]() є
гомоморфізмом алгебр
є
гомоморфізмом алгебр![]() та
та![]() .
Для кожної з заданих операцій маємо:
.
Для кожної з заданих операцій маємо:![]() ;
;![]() ;
;![]() .
Кожна з цих рівностей вірна для будь-яких
.
Кожна з цих рівностей вірна для будь-яких![]() за властивістю логарифмів. Доведемо,
що відображення
за властивістю логарифмів. Доведемо,
що відображення![]() є взаємно однозначним. Нехай
є взаємно однозначним. Нехай![]() ,
але
,
але![]() .
Тоді
.
Тоді
![]() .
.
Отримали
протиріччя. Отже, відображення
![]() є ізоморфізмом алгебр
є ізоморфізмом алгебр![]() та
та![]() .
.
Задача 5. Класифікувати алгебри:
a)
![]() ,
де
,
де
![]() – множина
квадратних матриць розмірності
– множина
квадратних матриць розмірності
![]() ;
;
b)
![]() .
.
Розв’язання.
Алгебра
![]() – некомутативний моноїд, оскільки
множина квадратних матриць
– некомутативний моноїд, оскільки
множина квадратних матриць
![]() є замкненою відносно множення; множення
матриць є асоціативною операцією.
Нейтральним елементом є одинична матриця
є замкненою відносно множення; множення
матриць є асоціативною операцією.
Нейтральним елементом є одинична матриця
![]() :
для довільної матриці
:
для довільної матриці![]() виконується рівність
виконується рівність![]() .
Ця алгебра не є групою, оскільки обернені
існують лише для невироджених матриць.
.
Ця алгебра не є групою, оскільки обернені
існують лише для невироджених матриць.
Розглянемо
алгебру
![]() .
Множина
.
Множина
![]() є
замкненою відносно множення (див. задачу
3), ця операція асоціативна і комутативна,
як множення дійсних чисел. Елемент 1 є
нейтральним, для кожного елемента існує
обернений:
є
замкненою відносно множення (див. задачу
3), ця операція асоціативна і комутативна,
як множення дійсних чисел. Елемент 1 є
нейтральним, для кожного елемента існує
обернений:
![]() .
Отже,
.
Отже,![]() – абелева група.
– абелева група.
A4
Чи будуть алгебраїчними операціями додавання, віднімання, множення та ділення, задані на: a)
 ;b)
;b)
 ?
?Нехай
 .
Вказати алгебраїчні операції та
визначити їх властивості, якщо:
.
Вказати алгебраїчні операції та
визначити їх властивості, якщо: ; с)
; с)
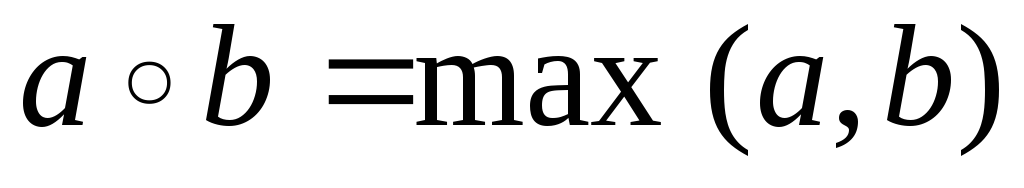 ;
; ; d)
; d)
 .
.
Нехай
 .
Знайти замикання множин
.
Знайти замикання множин
 .
.Скласти таблицю для закону композиції поворотів площини квадрата навколо його центру, при яких квадрат суміщається сам з собою.
Побудувати декілька підалгебр алгебри
 .
На прикладах з’ясувати,
чи буде підалгеброю
.
На прикладах з’ясувати,
чи буде підалгеброю
 та
та ,
де
,
де – деякі підалгебри.
– деякі підалгебри.Вказати систему твірних для алгебр: a)
 ;
b)
;
b)
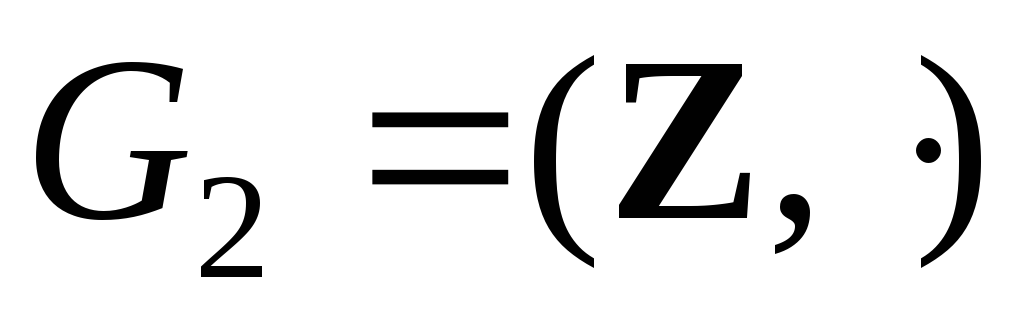 .
.З’ясувати, чи буде відображення
 гомоморфізмом алгебр
гомоморфізмом алгебр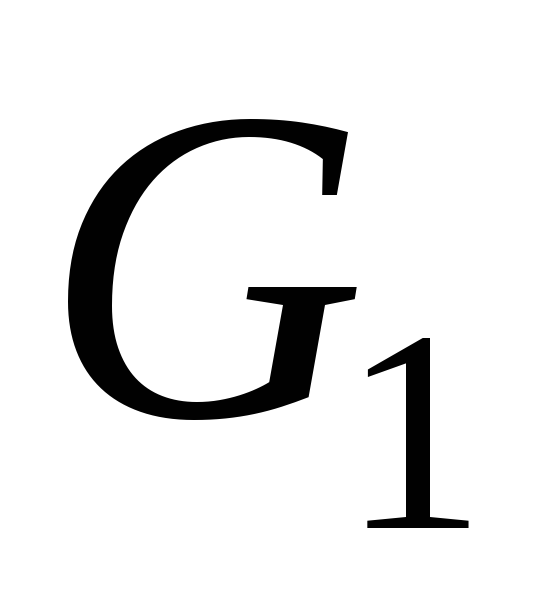 та
та ,
якщо:
,
якщо:
 ;
; ;
; .
.
Класифікувати тип алгебр:
 ;
с)
;
с)
 ;
e)
;
e)
 ;
; ;
d)
;
d)
 ;
f)
;
f)
 .
.
Чи буде абелевою групою алгебра
 ,
де
,
де
 .
.Класифікувати тип алгебр:
множина цілих чисел, кратних
 (
( ),
з операціями додавання та множенням;
),
з операціями додавання та множенням;множина квадратних матриць розмірності
 (
( )
з операціями додавання та множення;
)
з операціями додавання та множення;множина многочленів від однієї змінної скінченного степеня з дійсними коефіцієнтами з операціями додавання та множення;
множина раціональних чисел с операціями додавання та множення.
З’ясувати тип алгебри, носієм якої є множина
 і операції додавання та множення задані
таким чином:
і операції додавання та множення задані
таким чином:
![]() .
.
Знайти елементи, які мають обернені відносно множення.
Побудувати булеву алгебру на множині
 .
.
B4
Чи будуть алгебраїчними операціями додавання, віднімання, множення та ділення, задані на: a)
 ;b)
;b)
 ;c)
;c)
 ;
d)
;
d)
 ;e)
;e)
 ?
?З’ясувати, чи будуть алгебраїчними операціями додавання, віднімання, множення та ділення, задані на множині
 ,
де
,
де .
.З’ясувати, чи будуть алгебрами структури:
 ;
с)
;
с)
 .
. ;
;
З’ясувати, чи будуть асоціативними та комутативними операції, задані на
 :
: ; b)
; b)
 ;
c)
;
c)
 .
.
Вказати систему твірних для алгебри
 .
Чи буде системою твірних множина
векторів
.
Чи буде системою твірних множина
векторів ?
?Побудувати декілька підалгебр алгебри
 .
Чи може носієм підалгебри бути скінченна
множина?
.
Чи може носієм підалгебри бути скінченна
множина?Нехай
 – булеан
– булеан
 .
Побудувати дві підалгебри алгебри
.
Побудувати дві підалгебри алгебри
 .
.З’ясувати, чи буде відображення
 гомоморфізмом алгебр
гомоморфізмом алгебр та
та ,
якщо:
,
якщо:
 ;
; ;
; ,
де
,
де
 – скінченна множина,
– скінченна множина, – її булеан.
– її булеан.
Нехай
 ,
де
,
де – множина квадратних матриць
– множина квадратних матриць -го
порядку (
-го
порядку ( ),
), .
З’ясувати, які з відображень
.
З’ясувати, які з відображень є гомоморфізмами, якщо:a)
є гомоморфізмами, якщо:a)
 b)
b)
 c)
c)

З’ясувати тип алгебри:
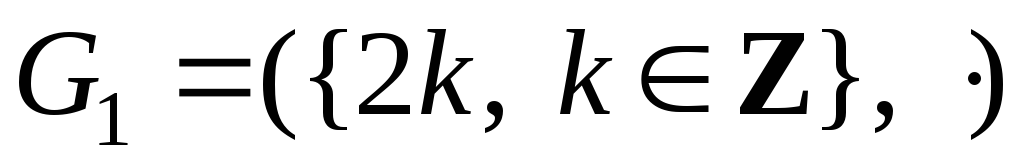 ; d)
; d)
 ;
; ; e)
; e)
 ,
де
,
де

 ; f)
; f)
 .
.
Чи буде абелевою групою алгебра
 ,
де
,
де
 .
.Скласти таблицю для закону композиції на множині рухів та відображень ромба, які суміщають ромб сам з собою. Побудувати алгебру, визначити її тип.
Задати множину підстановок множини
 .
Побудувати алгебру, визначити її тип,
виписати всі її підалебри.
.
Побудувати алгебру, визначити її тип,
виписати всі її підалебри.Класифікувати тип алгебр:
множина цілих чисел з операціями додавання та множенням;
множина комплексних чисел з операціями додавання та множення.
Чи утворює кільце відносно операції додавання та множення множина всіх дробів із знаменником 7?
Нехай задана множина матриць виду
 ,
де
,
де .
Визначити тип алгебри
.
Визначити тип алгебри .
.З’ясувати, чи буде булевою алгеброю
 ,
де
,
де
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нехай
 ,
де
,
де – множина квадратних матриць другого
порядку, елементами яких є цілі числа.
Нехай
– множина квадратних матриць другого
порядку, елементами яких є цілі числа.
Нехай
![]() .
.
Знайти
замикання
![]() .
.
Нехай
 ,
де
,
де – множина квадратних матриць другого
порядку, елементами яких є цілі числа.
Довести, що множина
– множина квадратних матриць другого
порядку, елементами яких є цілі числа.
Довести, що множина є системою твірних алгебри
є системою твірних алгебри
Нехай задана алгебра
 ,
де операція
,
де операція визначена наступним чином
визначена наступним чином
 Вказати підалгебри
Вказати підалгебри ,
з’ясувати, чи існують під- алгебри
,
з’ясувати, чи існують під- алгебри з двохелементним носієм. Чи буде алгебра
з двохелементним носієм. Чи буде алгебра півгрупою?
півгрупою?З’ясувати тип алгебри
 ,
де
,
де – множина векторів у трьохвимірному
просторі, а операція
– множина векторів у трьохвимірному
просторі, а операція – це векторний добуток.
– це векторний добуток.Нехай
 – булеан скінченної множини
– булеан скінченної множини .
З’ясувати
тип алгебри:
.
З’ясувати
тип алгебри:
 ; с)
; с)
 ;
; ; d)
; d)
 .
.
Нехай
 .
Задати операцію на множині
.
Задати операцію на множині таким чином, щоб алгебра
таким чином, щоб алгебра була:
була:
a) групоїдом; b) півгрупою; c) моноїдом; d) групою.
З‘ясувати, чи будуть групами наступні множини функцій з операцією суперпозиції:
 ,
де
,
де

 ;
; ,
де
,
де

 .
.
Нехай задана множина матриць виду
 ,
де
,
де ,
,
 .
Визначити тип алгебри
.
Визначити тип алгебри
 .
.З’ясувати тип алгебри:
 ,
де
,
де – класи лишків за модулем
– класи лишків за модулем ,
, і
і – додавання та множення за модулем
– додавання та множення за модулем відповідно, якщо:a)
відповідно, якщо:a)
 ;
b)
;
b)
 .
.
