8. Конкуренция в широком смысле или интерференция (-, -)

Конкуренцией в широком смысле (предпочтительнее употреблять термин «интерференция») называют любое взаимно отрицательное отношение между видами. Её частными случаями являются: 1)конкуренция(в узком смысле слова) за тот или иной ограниченный ресурс (соперничество); 2) взаимное аллелопатическоеингибирование(антагонизм) и 3) непосредственная «борьба» между представителями разных видов (агрессия).

Вначале рассмотрим простейшую модель взаимодействия двух видов в условиях конкуренции за общий ресурс (пищу). Выразим коэффициент прироста каждой из популяций в виде

r_i = - (i = 1, 2),

где – положительный коэффициент, характеризующий потребность в пище каждого из видов;F(x_1, x₂) – скорость потребления пищи. Предположим, что функцияF(x_1, x₂) обращается в нуль приx₁ = 0 иx₂ = 0 и монотонно неограниченно возрастает по каждой из переменных.

Тогда динамика развития популяций может быть описана системой дифференциальных уравнений

.

Перепишем её в виде

.

Исключая отсюда функцию F(x₁,x₂), получим

или

.

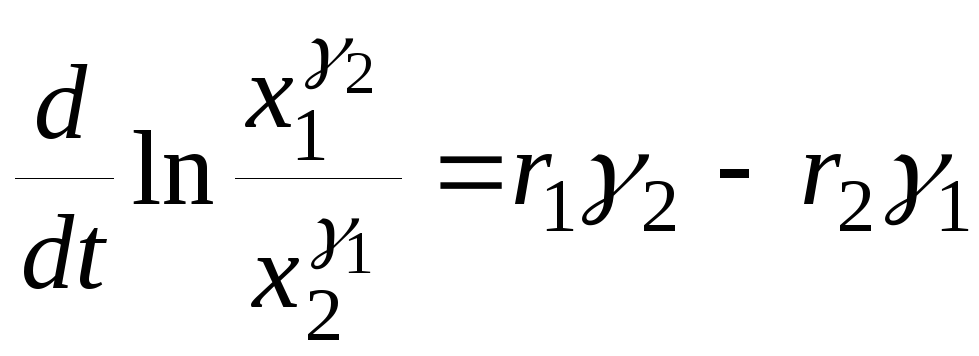Решение этого уравнения имеет вид

,

где и– численности популяций в начальный момент времениt= 0.

Прежде всего, следует отметить, что указанные решения системы должны быть ограничены на бесконечности, то есть при . Это связано с тем, что в силу монотонного неограниченного возрастания функциипо каждой из переменной приобязательно наступит момент, когда скорость измененияx_iстанет меньше нуля, то естьx_i начнет убывать.

.

Для дальнейшего анализа полученного решения положим для определенности, что . Тогда отношениебудет бесконечно возрастать, то есть. Отсюда в силу ограниченностиx₁иx₂получаем, что.

Это означает, что численность второй популяции, для которой значение меньше, убывает, стремясь к нулю, в то время, как численность первой стремится к значению, определяемому из уравнения. Это подтверждает интуитивный вывод о том, что исчезает вид, обладающий меньшим коэффициентом естественного прироста и более чувствительный к нехватке пищи.

Полученные результаты также подтверждают известный принцип Гаузе, согласно которому два вида с одинаковыми экологическими потребностями не могут сосуществовать в одном месте обитания.

Необязательно два конкурирующих вида не могут сосуществовать вместе и один из видов должен исчезнуть. Указанный результат был получен для простейшей модели, не учитывающей саморегуляциючисленности видов. Рассмотрим случайконкуренции с саморегуляцией, описываемойлогистическимуравнением, когда взаимодействие видов несимметрично и описывается линейной функцией вида

;.

Это так называемая модель Лотки-Вольтерра для двухвидовой системы с конкуренцией

где r_i – удельная скорость роста иK_i– ёмкость среды дляi-го вида при отсутствии конкуренции, а положительные безразмерные коэффициентыа₁₂иа₂₁служат мерой относительного влияния видов друг на друга;(i=1,2;ij).

Поведение решений данной системы удобно охарактеризовать с помощью метода фазовых портретов на плоскости с координатами (x₁,x₂). В каждой точке траектории решения (x₁(t),x₂(t)) на фазовой плоскости может быть отображён вектор скорости, имеющий координаты , то есть правые части системы дифференциальныхуравненийопределяют вектор скорости.

Как видно из указанной системы, знаки производных dx₁/dtиdx₂/dt совпадают со знаками линейных функций

l₁(x₁, x₂) = k₁ - x₁ - a₁₂x₂

l₂(x₁, x₂) = k₂ - x₂ - a₂₁x₁

и эти же линейные функции определяют на фазовой плоскости геометрическое место точек, где указанные производные обращаются в нуль, в виде линейных уравнений:

l1(x1, x2) = k1 - x1 - a12x2 = 0  x1 = k1 - a12x2

l2(x1, x2) = k2 - x2 - a21x1 = 0  x2 = k2 - a21x1 .

При этом производная будет положительнойподпрямойl_i(x₁,x₂) = 0, равной нулю – на прямой, и отрицательной – над ней. Используя эти данные, в каждой точке (x₁,x₂) мы можем качественно определить направление движения на проходящей через неё траектории.

Если пренебречь вырожденными случаями параллельности и совпадения, то возможны следующие четыре варианта взаимного расположения прямых l₁иl₂на фазовой плоскости:

1. Прямая l₁располагается целиком вышеl₂, то естьи, что эквивалентнои. Первый вид как более сильный конкурент всегда будет вытеснять второй, независимо от их начальныхчисленностей ().

2. Прямаяl₂целиком лежит вышеl₁, то естьи, что эквивалентнои. Всегда побеждает второй вид.

3. Прямые l₁иl₂пересекаются в положительном квадранте и при этомl₁падает круче, чемl₂, то естьи, что эквивалентнои. Существует единственное положениеравновесия (),координаты которого удовлетворяют системе линейных уравнений

и равны

и которое устойчиво, так что из любого начального состояния система с течением времени переходит в равновесноесостояние (),характеризуемое нулевыми численностями обоих видов.

4. Прямые l₁иl₂пересекаются в положительном квадранте так, чтоl₂падает круче, чемl₁то естьи, что эквивалентнои. Исход конкуренции определяется начальным соотношением численностей, в зависимости от начального соотношения плотностей произойдёт вытеснение первого или второго вида.