теория погрешностей

F При измерении временного интервала с помощью секундомера (цена деления ω= 0.1 с) получено значение 32.8 с. Тогда предельная погрешность (см. формулу (11)):

пред1 = 0.001 32.8+0.1= 0.1328 (с) и

σприб ≈ 0.1328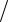3 ≈ 0.0443 (с).

Для механических приборов (линейка, штангенциркуль, микрометр, динамометр и т.п.), к которым нет паспорта, можно считать, что

(12 ) пред ≈ ω,

где ω – цена наименьшего деления прибора (с учетом нониуса).

В некоторых механических приборах (штангенциркуль, микрометр) используется нониус – специальное устройство в виде дополнительной подвижной шкалы с делениями, размер которых меньше размера наименьшего деления основной шкалы, что позволяет

деления шкалы нониуса. Для определения точности нониуса необходимо совместить начальный (нулевой) штрих нониуса с какимлибо штрихом основной шкалы (будем его также называть нулевым). При этом (k +1)-й штрих на шкале нониуса совпадет с (k)-м штрихом

на основной шкале. Тогда точность нониуса ω определяется в зависимости от цены деления основной шкалы ω по формуле

(13 ) ω = ω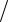k .

Обычно для штангенциркуля цена наименьшего деления основной шкалы ω составляет 1 мм, а цена деления шкалы нониуса – 0.9 мм. В этом случае 11-й штрих нониуса совпадет с 10-м штрихом основной шкалы, то есть точность нониуса равна 0.1 мм.

Отсчет по шкале, снабженной нониусом, осуществляется следующим образом. Если начальный штрих нониуса точно совпадает с каким-либо штрихом основной шкалы, то измеряемое значение соответствует этому значению на основной шкале. Если начальный штрих нониуса попадает между двумя штрихами основной шкалы, то надо сначала определить, какой из штрихов нониуса совпадает с одним из штрихов основной шкалы (например, пусть совпадает m-й штрих нониуса). Тогда измеряемое значение равно отсчету, соответствующему меньшему из двух штрихов на основной шкале, сложенному с произведением ω m.

Пример (продолжение).

21

H При измерении диметра шара с помощью штангенциркуля, для которого ω= 0.05мм, нулевое деление нониуса оказалось между делениями 12 и 13 мм на основной шкале, а 6-й штрих нониуса совпал с одним из делений основной шкалы. Тогда искомый диаметр равен 12 +0.05 6 =12.3 (мм), а предельная

погрешность пред ≈ ω = 0.05 мм.

Погрешность взвешивания. Определение погрешности при использовании рычажных весов имеет свою специфику. Прежде всего, взвешивание, как правило, производят разовое, сводя, таким образом, прямое измерение к приборной погрешности. Приборная погрешность состоит из трех слагаемых: предельной погрешности подбора наименьшей гири пред.подбора , суммарной предельной погрешности всех гирь, участвующих в измерении, пред.гирь , и предельной погрешности весов пред.весов , (два последних слагаемых

связаны соответственно с точностью изготовления гирь и качеством исполнения основных трущихся элементов весов: опорной пластины, призмы и коромысла).

Предельная погрешность подбора наименьшей гири

Дпред.подбора аналогична погрешности отсчета и равна половине массы наименьшей гири, лежащей на уравновешенных весах, либо выводящей весы из равновесия.

Суммарная предельная погрешность всех гирь пред.гирь

учитывает каждое значение из набора гирь, которым удалось уравновесить чашки весов. Например, разновес Г4-211 стандартных лабораторных весов имеет следующую зависимость величины погрешности от номинального значения гири:

22

субъективная погрешность учитывается посредством оценки стандартного отклонения

(15а) σ′суб = 0.3 β,

где β – цена деления шкалы прибора, выраженная в градусах.

* * * * * * *

Погрешность метода. Систематическая погрешность метода может быть учтена в результате тщательного анализа модельных представлений, положенных в основу процесса измерений, в виде оценки стандартного отклонения σмет .

* * * * * * *

Суммарная систематическая погрешность σсист в

предположении о независимости возникновения ее составляющих вычисляется по формуле:

(16 ) σсист = σприб2 + σокр2 + σсуб2 + σмет2 .

При выполнении лабораторных работ в курсе "Общая физика" погрешность метода σмет обычно принимают равной нулю, поэтому пользуются усеченной формулой для σсист :

Стьюдента, используемого для оценки доверительного интервала для случайных погрешностей). Значения коэффициента Чебышева γα при

различных коэффициентах доверия б приведены в таблице № 2.

* * * * * * *

Пример 1 (продолжение 2).

24

Оценка систематической погрешности, проведенная студентом Ивановым, дала следующие результаты:

1) предельная погрешность для секундомера пред. (см. формулу (11)) и стандартное отклонение σприб. (согласно (4)) для погрешности прибора соответственно равны 0.1 с и 0.033 с;

2)стандартное отклонение для погрешности округления (в соответствии с (14)) σокр. ≈ 0.03 с;

3)стандартное отклонение для субъективной погрешности согласно (15) σсуб. ≈ 0.3 сs ;

4)итоговая систематическая погрешность в соответствии с формулой (16а):

σсист = 0.0332 +0.032 +0.32 ≈ 0.3(с).

Если бы целью Иванова было бы получение оценки периода с учетом только систематической погрешности, то он далее проделал бы следующие вычисления (как один из вариантов): выбрал бы значение коэффициента доверия α = 0.95 , по таблице №2 нашел бы значение коэффициента Чебышева γα = 4.47 и определил бы

доверительный интервал согласно (17):

сист = 4.47 0.3= 1.34 (с).

Окончательно студент Иванов представил бы следующий результат (с учетом только систематической погрешности):

T =(4.6 ±1.3) c , коэффициент доверия α = 0.95 .

Продолжение следует

* * * * * * * * * * * * * * *

§3.3. Суммарные (случайные и систематические) погрешности прямых измерений

В предположении о независимости возникновения случайных и систематических погрешностей для величины стандартного отклонения суммарной погрешности выборочного среднего значения x используется следующая формула:

25

Доверительный интервал для суммарной погрешности можно вычислить, воспользовавшись, как и в формуле (17), коэффициентом Чебышева

выборочное стандартное отклонение среднего арифметического S x

стремится к нулю как 1 n , в то время как систематическая составляющая погрешности измерения остается неизменной. Отсюда можно сделать очень важный вывод: уменьшать величину S x с

помощью многократных измерений следует только до тех пор, пока еще вклад случайной погрешности в общую погрешность больше вклада от систематических погрешностей.

* * * * * * *

Пример 1 (продолжение 3).

Для оценки суммарной погрешности (18) Иванов проделал

учетом суммарной погрешности):

T =(4.6 ±1.4) c , коэффициент доверия α = 0.95 .

Вывод, который должен сделать студент Иванов: проведение измерений коротких временных интервалов периода колебаний математического маятника с помощью ручного секундомера приводит к большим относительным погрешностям (1.44.6 100% ≈30%).

Вывод, который сделает преподаватель, увидев результаты Иванова: Иванов плохо продумал методику проведения измерений, и, несмотря на значительные усилия, затраченные на проведение экспериментов и расчет результатов, не заслуживает оценки выше, чем "удовлетворительно".

Продолжение следует

* * * * * * * * * * * * * * *

§3.4. Погрешность прямых однократных измерений

Очень часто при выполнении лабораторных работ ту или иную физическую величину измеряют лишь однократно. Такие ситуации

26

продиктованы, как правило, нецелесообразностью многократных измерений какой-либо величины или недостатками методики проведения многочисленных измерений. Характерный пример, связанный с процедурой взвешивания тела, приведен в подразделе «б) систематические погрешности». Аналогично, при измерении длины нити математического маятника (см. пример 2) нет необходимости (в рамках рассматриваемой модели) проводить больше одного измерения.

В приведенных и подобных случаях вычисление погрешности сводится к вычислению систематической погрешности, то есть использованию формул (16) и (17) для расчета стандартного отклонения и доверительного интервала соответственно. Количество слагаемых, учитываемых в формуле (16), определяется конкретным случаем проведения измерения, однако в большинстве случаев достаточно ограничиться приборной погрешностью (см. формулу (4)) и погрешностью округления согласно (14). Так, в уже рассматриваемом примере с длиной математического маятника для стандартного отклонения усист имеем:

значению α. При отсутствии коэффициента доверия α в записи величины С коэффициент Чебышева γα выбирается

равным γα = 4,47 , то есть соответствующим α = 0,95 .

***** §3 *****

27

§4. Основные правила обработки результатов косвенных измерений

выборочного стандартного отклонения Su случайных и стандартного отклонения уu систематических ошибок,

вычисляемых по формулам:

Для оценки случайной относительной погрешности удобно использовать относительное стандартное отклонение δu = Suu .

Доверительный интервал как для случайных, так и для систематических погрешностей может быть рассчитан в общем случае с использованием коэффициента Чебышева γα :

Для оценки суммарной погрешности стандартного отклонения можно использовать такую же формулу, как и для прямых измерений:

( 25 ) σсумм = Su2 + σu2 .

28

Для оценки суммарной относительной погрешности удобно использовать относительное стандартное отклонение δu = σсуммu .

Вычисление доверительного интервала для суммарной погрешности проводится также с использованием коэффициента Чебышева γα :

следующие результаты:

ti = 232.6, 233.4, 232.9, 232.8, 233.2 (c).

Для нахождения оценок периода колебаний он сначала вычислил среднее арифметическое (согласно (1)) по всем результатам прямых измерений:

t =1164.9 5 = 232.98 (c)

29

3)стандартное отклонение для субъективной погрешности согласно (15) σсуб ≈ 0.3 с.

4)итоговая систематическая погрешность в соответствии с формулой (16а)

σ t ,сист = 0.1112 +0.032 +0.32 ≈ 0.321(с).

Тогда для периода колебаний из формулы (22) следует, что

σ T ,сист = σ t ,сист N = 0.321 0.02 ≈ 0.006 (с).

Таким образом, для суммарной погрешности (см. формулу (25)) студент получил

σсумм = S2T + σ2T ,сист = 0.00292 + 0.0062 ≈ 0.0067 (c).

Для α = 0.95 и γα = 4.47 в соответствии с (26) получена оценка

доверительного интервала

сумм = γα σсумм = 4.47 0.0067 ≈ 0.030(с).

Окончательно студент Петров представил следующий результат: T =(4.66 ±0.03)с, коэффициент доверия α = 0.95, δT ≈ 6%.

Заметим, что результат, полученный Петровым, существенно точнее результата, представленного студентом Ивановым, и студент Петров может заслуженно надеяться на более высокую оценку своей работы, чем Иванов.

Продолжение следует

* * * * * * * * * * * * * * *

§4.2. Частныеслучаиобработки результатов косвенных измерений

Довольно часто возникает ситуация, когда косвенно измеряемая величина u является функцией других косвенно

измеряемых величин υ,..., w , то есть u = f (υ,..., w). В этом случае можно поступить одним из следующих способов.

1.Если величины υ,..., w независимы, то есть каждая из них

является функцией своих прямо измеряемых величин, то для получения оценок как самой физической величины u , так и ее стандартного отклонения применяются те же формулы, что и в случае прямых измерений величин υ,..., w . Иными

словами, требуемые оценки для величин υ,..., w находятся, как и положено, по формулам косвенных измерений, а затем

30