2.0.Моделирование функции преобразования средства измерения
2.1. Задание № 1. Чувствительность средства измерения.
Чувствительность по определению:
.
Найдём чувствительность СИ как производную функции преобразования:
2.2. Задание № 2. Определение погрешностей в виде касательной.
Определить абсолютную, относительную и приведенную погрешности нелинейности при аппроксимации функции преобразования СИ в виде касательной в начальной точке. Определить наибольшую погрешность нелинейности.
Запишем уравнение касательной к графику функции преобразования в начальной точке:
Найдём y΄(x0):
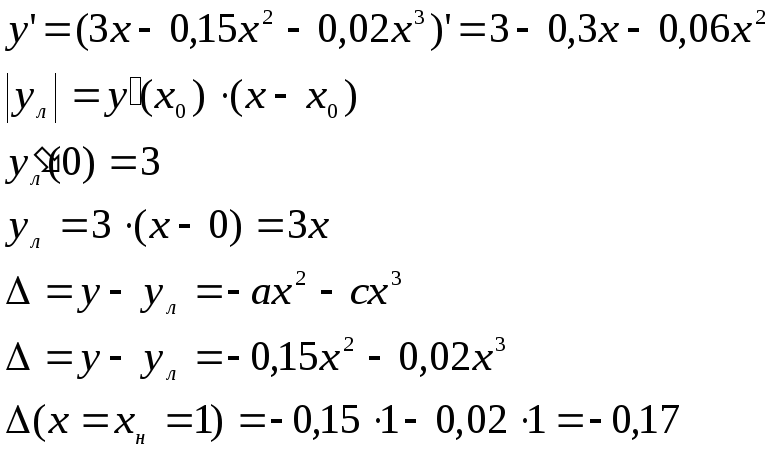
Найдём y΄(x0):
Получаем:
Ответ: уравнение
линейной функции преобразования
.
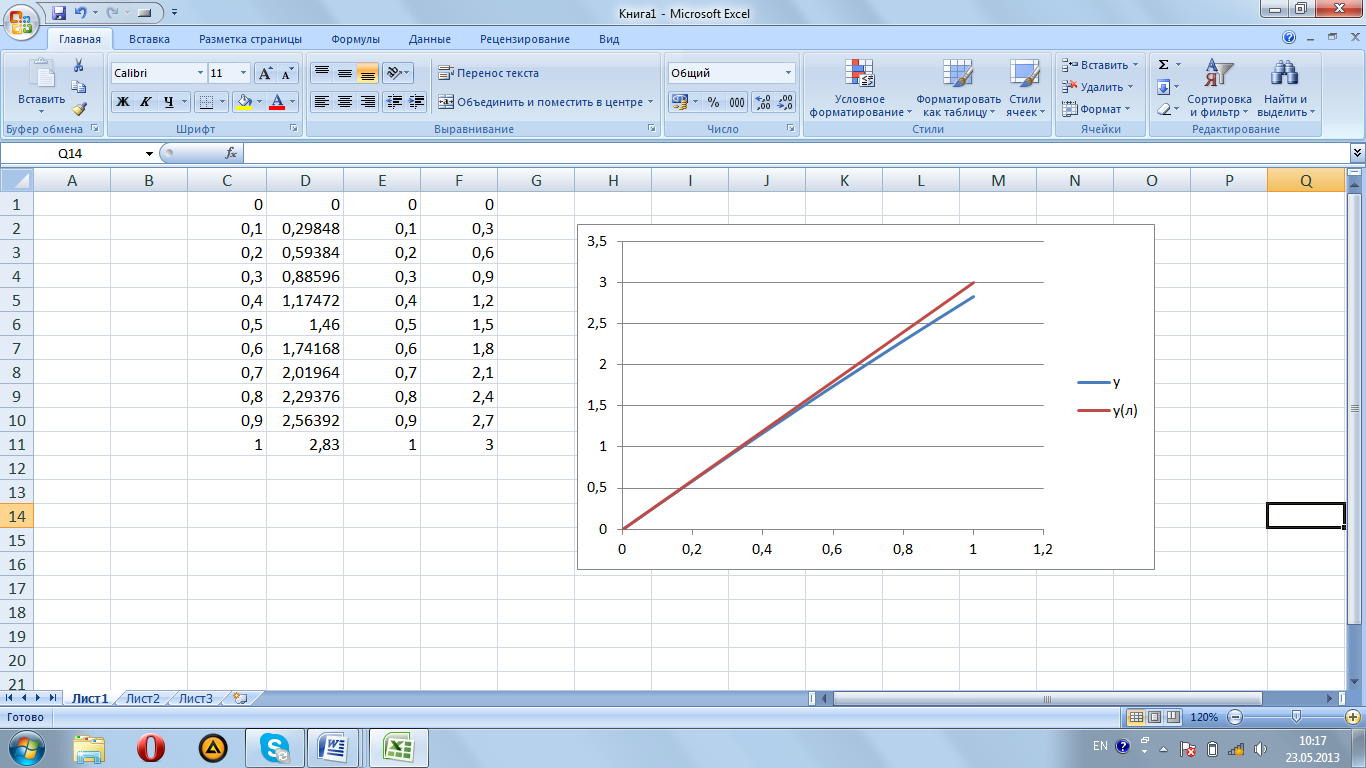
Найдём абсолютную погрешность линеаризации:
Т.к.
,
то абсолютная погрешность линеаризации
принимает отрицательное значение:
В конечной точке наибольшая по модулю абсолютная погрешность:
В конечной точке наибольшая по модулю относительная погрешность:
Найдём приведённую погрешность:
2.3. Задание № 3. Определение погрешностей в виде хорды.
Определить абсолютную и относительную погрешности нелинейности при аппроксимации функции преобразования СИ в виде хорды, проходящей через начальную и конечную точки диапазона измерения. Определить наибольшую погрешность нелинейности.
Аппроксимируем
функцию преобразования
СИ хордой, проходящей через начальную
[x0
; y0]
= [0 ; k]
и конечную [xн
; yн]
= [1 ;
]
точки диапазона измерения:
Найдём уравнение хорды, записав уравнение прямой, проходящей через две точки:
Подставляем:
Выразим
:
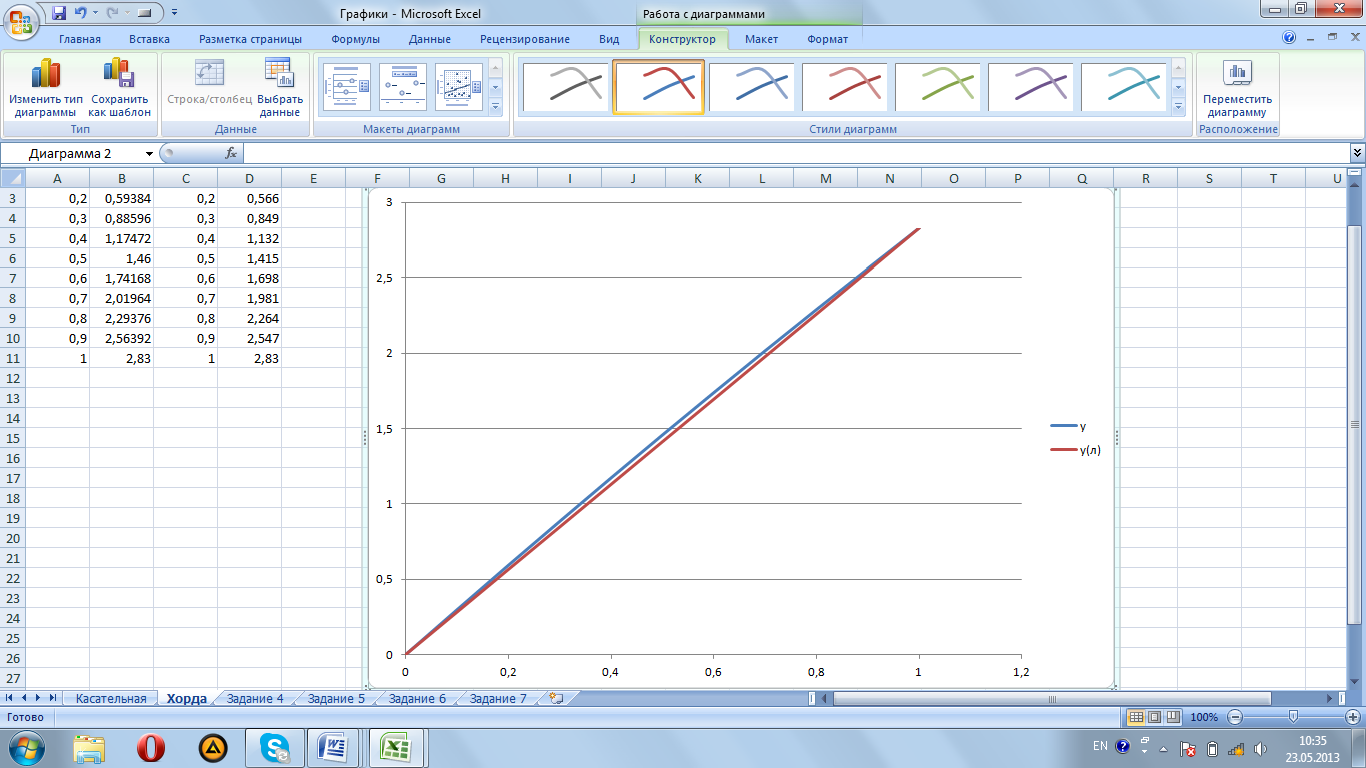
Определим абсолютную погрешность нелинейности:
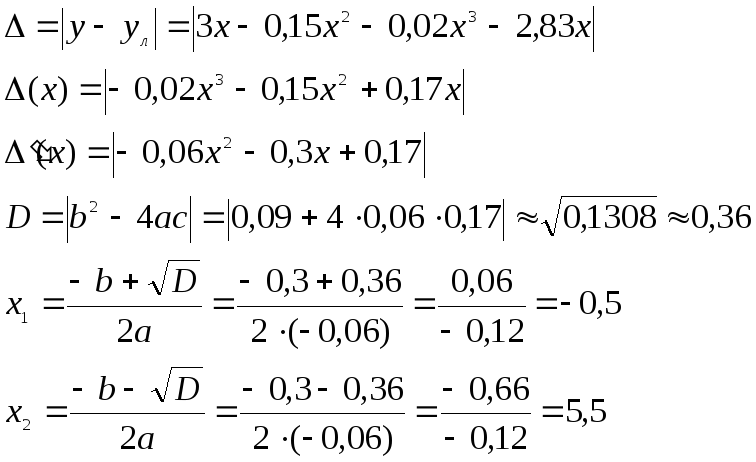
Т.к.
,
то корень равный 5,5 не удовлетворяет
условию задачи.
Найдём точку, в которой абсолютная погрешность принимает наибольшее значение:
Корень x = 0,5 принадлежит диапазону измерения [0 ; 1].
При x = 0,5 абсолютная погрешность принимает наибольшее значение. Найдём это значение:
Определим относительную погрешность нелинейности:
Наибольшее значение
относительная погрешность принимает
в точке
.
Найдем его:
2.4. Задание № 4. Определение погрешностей функции .
Аппроксимировать
функцию преобразования СИ на интервале:
линейной функцией вида:
,
так, чтобы наибольшая погрешность
линеаризации была минимальна:
.
Определить предельные относительную
и приведенную погрешности линеаризации.
Аппроксимируем
функцию преобразования
СИ на интервале [0 ;xн]
= [0 ; 1] линейной функцией yл
= E·x
+ k:
Запишем выражение для абсолютной погрешности:
Приравняв производную абсолютной погрешности по x к нулю, найдём точки, в которых абсолютная погрешность имеет экстремумы:
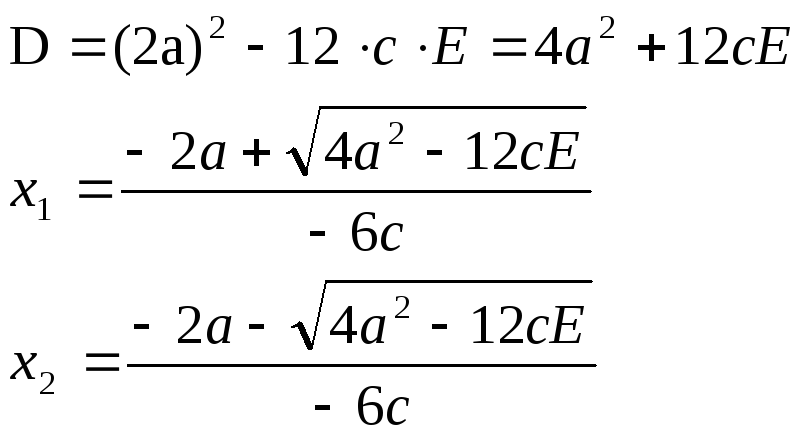
По условию задачи
подходит точка x2
(во втором случае x1
< 0, т.к. a
>0, c
>0, E
< 0,
)
Найдём погрешность в точке xэкс = x2:
Найдём погрешность в точке xн = 1:
Оптимизируем решение:
т.к. секущая пересекает функцию преобразования, то погрешности линеаризации в точках xн и xэкс будут разных знаков:
Решим уравнение в Mathcad относительно E:
Получаем,
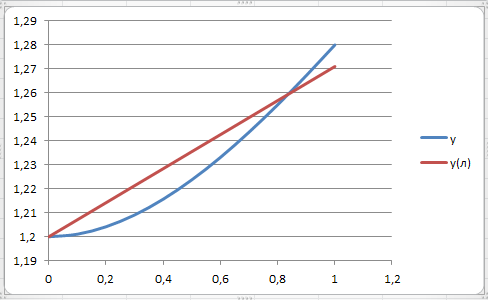
Абсолютная погрешность линеаризации примет вид:
Предельное значение абсолютной погрешности равно:
Относительная погрешность линеаризации имеет вид:
Предельное значение относительной погрешности равно:
Найдём приведённую погрешность линеаризации:
