Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4624 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Красноярский государственный аграрный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

учеб реология Арет

.pdf
Скачиваний:
82
Добавлен:
15.03.2016
Размер:
2.21 Mб
Скачать
☆

191

192

Сопротивление движению лопасти мешалки в нелинейно – вязкой жидкости

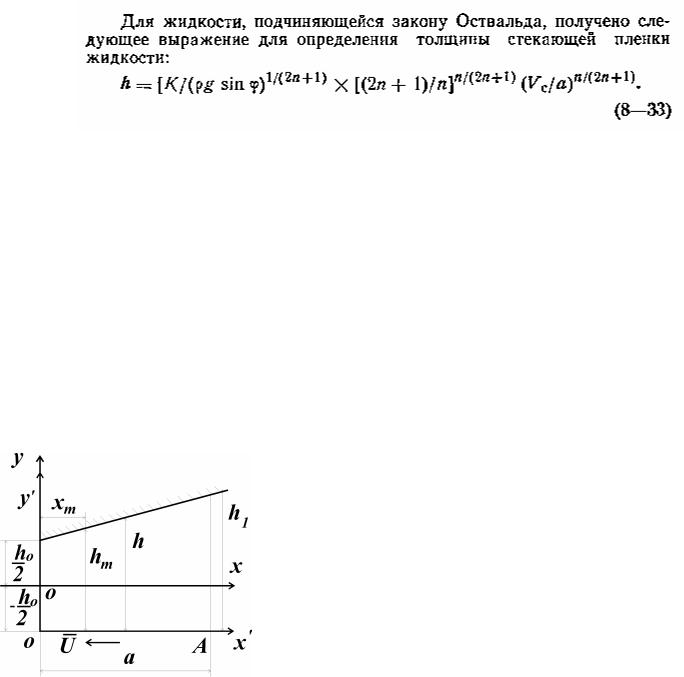
1. Определение распределения давления потока на пластину Рассмотрим задачу (рис. 1), полагая наклон верхней пластины (лопасть мешалки)

незначительным, и, в случае обращённого движения, задавая скорость перемещения нижней горизонтальной пластины в отрицательном направлении оси x.

В общем виде проекция уравнения движения на ось x

имеет вид:

v

 

vx

v

 

vy

v

 

vz

v

p

 

 

 

yx

 

 

 

 

(1)

 

x

 

 

x

 

x

z

 

 

 

xx

 

 

zx

qx,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t

 

x

 

y

 

z

x

x

 

y

 

z

 

где - плотность,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t -

время,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

vx, vy , vz

- проекции скорости частицы жидкости на, соответственно, оси x,

 

 

 

 

y, z,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p -

 

давление,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

193

xx, yx, zx - касательные напряжения на площадках, перпендикулярных

первому индексу в направлении второго индекса,

 

 

 

 

 

 

 

 

 

qx - проекция ускорения свободного падения на ось x.

 

 

 

 

 

 

 

В силу горизонтальности оси x qx 0 ; пусть поток стационарный, тогда

 

vx

0; из-за

 

 

 

 

 

 

 

 

 

 

 

 

 

t

малого наклона верхней пластины и ламинарности потока

 

vx

0 . Полагаем, что

 

 

 

 

 

 

 

 

x

 

 

 

 

 

компоненты скорости по осям y и z отсутствуют vz vy

0 Полагаем также, что

напряжения сдвига не меняются в направлениях x и z

 

 

 

 

 

 

 

. Тогда на-

 

 

xx

 

 

 

zx

0

 

 

x

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

пряжение сдвига yx будет функцией координаты y и, опуская индексы при напря-

жениях, получим из (1) уравнение движения равновесия вида:

 

 

 

 

 

 

 

p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

или, приняв (y) 1 (y) 2 (y),

 

 

 

d 1

 

d 2

 

d p

;

 

d 1

 

d p

;

d 2

0

 

 

 

 

 

 

 

 

d y d y dx

 

 

 

d y dx

dy

(2)

(3)

(4)

Физически это означает разбиение задачи на две: течение между неподвиж-

ными пластинами под действием перепада давлений и течение под действием дви-

жения нижней пластины при отсутствии перепада давлений.

Пусть жидкость подчиняется степенному закону

0

 

 

 

n 1

0

 

 

 

 

 

n 1

 

(5)

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

0

 

 

 

 

 

 

где -

коэффициент динамической вязкости,

 

- скорость сдвига, здесь

dvx

;

 

 

 

dy

194

0 ,

 

 

 

 

 

 

0 - напряжение сдвига и скорость сдвига при произвольно выбранном

приведённом состоянии течения. Обычно принимают

 

1

;

 

 

0 1с

 

 

 

0

 

 

 

 

;

- коэффициент динамической вязкости при скорости сдвига

0

n – реологическая константа жидкости (индекс течения).

 

 

 

Часто реологический степенной закон представляют в виде

 

 

 

n

 

 

 

 

(6)

 

 

 

 

 

 

где - реологическая константа жидкости, коэффициент консистенции.

Сравнение формул (5) и (6) даёт

 

 

 

0

 

 

 

 

 

(7)

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

Интегрируя уравнение (4) для 1 , получим

 

 

1

 

d p

y C1

 

 

(8)

 

 

 

 

 

 

 

 

 

d x

 

 

 

 

 

В силу симметрии потока при y 0

1 0

и C1 0.

Реологическое уравнение можно записать в виде:

 

 

 

 

 

 

dvx

 

 

 

(9)

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d y

 

 

 

 

 

1

и используя закон (5), получим

 

Приняв 0

 

 

1

 

 

 

 

 

dv x

n

 

(10)

 

0

 

1

 

 

 

 

 

 

 

 

 

 

d y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда из выражений )10) и (8) получим

195

 

 

 

1

 

 

d p

1

 

 

1

 

 

 

 

 

 

(11)

dv x 1

 

 

 

y

 

 

 

 

d y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

n

 

 

 

 

 

 

 

 

0

d x

 

 

 

 

 

 

 

 

 

 

 

 

и

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

n 1

 

 

 

 

 

n

 

 

1

 

d p

 

 

 

 

 

 

 

 

 

n

 

 

 

(12)

v x1

 

 

y

 

 

C

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

n 1

0

 

d x

 

 

 

 

 

 

По условию прилипаемости жидкости к неподвижным стенкам канала запишем:

y

h

;

v x 1 0

(13)

 

2

 

 

 

Определив по условиям (13) константу интегрирования C 2 , запишем

 

 

 

n

 

1 d p

1

 

 

 

 

n 1

 

 

 

h

n 1

 

(14)

v x 1

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n 1

 

 

 

 

 

 

d x

 

n

 

 

 

 

 

 

n

 

 

 

2

 

 

n

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

или, в силу равенства

 

 

y y

h

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

1 d p

 

1

 

 

 

 

 

 

h

 

 

n 1

 

 

 

h

 

n 1

 

(15)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

v x 1

 

 

 

 

 

n

 

 

 

 

 

 

y

 

 

 

 

 

n

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

n 1

 

0 d x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Проведём преобразование и интегрирование для потока под действием движения нижней пластины:

d

2

 

d

 

 

dv x

2

 

 

 

dv x

2

 

 

 

 

0 ;

 

 

 

 

 

0

;

 

 

C 3

;

 

 

 

 

 

 

 

d y

d y

 

d y

 

 

d y

 

 

 

 

 

 

 

 

 

 

 

 

(16)

 

dv x

 

n

 

dv x

 

 

 

C

 

 

1

 

 

 

 

 

2

 

2

 

3

 

 

 

 

 

 

 

 

 

C 3 ;

 

 

 

 

 

n

C 4

;

v x 2 C 4 y

C 5

 

 

 

 

 

 

0

d y

 

 

d y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

196

Запишем краевые условия и определим константы интегрирования C 4 и C 5 :

v

 

 

 

 

h

 

u

;v

 

 

h

 

 

 

 

 

h

 

;

 

 

 

 

 

 

 

 

0 ;

u C

 

 

C

 

 

x 2

 

 

 

2

 

 

x 2 2

 

 

 

 

4

2

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(17)

0 C 4

 

h

C

5 ;

C 5

 

u

;

C 4

 

u

 

 

 

 

 

 

 

2

 

h

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

Тогда, при y y h

2

u

v x h h y

И по принципу адитивности решений получим

 

 

n

 

1

 

d p

1

 

 

 

h

 

n 1

h

n 1

 

 

 

 

 

 

 

 

 

 

 

 

v x v x 1 v x 2

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

n

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d x

 

 

y

 

 

 

 

 

 

 

n 1

 

0

 

 

 

 

 

2

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(18)

u

h y

(19)

 

h

 

Далее продолжим решение в линейной постановке, аналогичной задаче Рейнольдса

– Релея 1 .

При n 1 получим из выражения (19)

 

 

 

1

 

d p

 

 

 

 

u

 

 

 

 

 

 

 

 

 

 

v

x

 

 

 

y 2

y h

 

h y

(20)

 

 

 

 

 

 

2 0

 

d x

 

 

 

h

 

 

 

 

 

 

 

 

 

 

 

 

Полагая расход через любое поперечное сечение щели постоянным, запишем :

h

v x d y C 6

0

197

Подставив скорость v x по формуле (20) в (21) и проведя интегрирование, получим

h3

 

d p

 

 

 

 

uh

C 6

6 0

 

 

d x

 

(22)

На участке x 0 a в некоторой точке x m

выполняется условие

d p

0. Пусть значе-

 

 

 

d x

нию x m соответствует ширина щели hm , тогда из выражения (22) следует C 6 U hm

и можно записать зависимость (22) в виде:

 

 

 

 

d p

6 0 u

(h hm )

 

 

 

 

 

 

 

 

 

 

 

 

h3

 

 

 

 

d x

 

 

 

 

 

 

 

(23)

 

Из геометрических соображений (рис. 1) свяжем переменные x и h :

 

 

 

 

x

(24)

 

h h0

1 k

 

 

 

 

 

 

 

a

 

 

Тогда левую часть уравнения (23) можно преобразовать так:

d p d p d h k h0 d p d x dh d x a d h

(25)

Подставив выражения (25) в (23) и разделив переменные, получим:

d p

6 0 ua

h 2

h m h 3 d h,

(26)

 

 

kh0

 

 

198

p

6

0

ua

h 1

h

m

h 2

 

C 7

(27)

 

 

 

 

 

kh0

2

 

 

 

 

 

 

 

Полагая, что давление вне зазора равно p 0 , запишем условия:

p p 0

при h h0

и h h1 h0 1 k

(28)

Условия (28) и выражение (27) дают систему уравнений для нахождения констант

hm

C 7 :

 

 

6

0 ua

 

1

 

hm

 

 

p 0

 

 

 

 

C 7

 

 

 

 

2

 

 

h0

 

 

 

kh0

 

 

2h

0

 

 

(29)

 

 

6

0

ua

1

 

 

 

 

hm

 

 

p 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

kh

 

 

1 k

1 k

2

 

 

0 h0

 

2h

0

 

 

Решая систему (29) и опуская выкладки, получим

hm 2h0

1 k

(30)

2 k

 

 

и

C

7 p

0

6

0 ua

 

1

(31)

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

kh0

 

 

 

 

 

 

 

2 k

 

Подставляя значения констант hm

и

С 7

по формулам (30) и (31) в формулу (27), по-

лучим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

199

p (h) p 0

 

6 0 ua h

0

 

1

 

h

0

2 1 k

(32)

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

kho

 

h

2 k

 

h

2 k

 

В силу связи (24) между переменными

 

h

 

и

x получим

 

 

h0

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

(33)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ha k x

ииз формулы (32) получим распределение давления потока на пластину:

p x p 0

 

6

0 u a

a

1

 

1 k

a 2

 

 

(34)

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a k x

 

 

 

a k x

 

 

 

 

 

kh0

2 k

2 k

 

 

 

2. Определение подъёмной силы, действующей на лопасть мешалки.

Теперь можно рассмотреть подъёмную силу R , действующую на пластину:

a

6

ua

a

a

1

 

1 k

a 2

 

 

 

R p p 0 dx

 

0

 

 

 

 

 

 

 

 

 

 

 

(35)

kh

2

 

2 k

 

a kx

2

a

0

0 a kx

 

2 k

 

 

 

В результате интегрирования получим

 

6

0U

a

2

 

2k

 

 

R

 

ln 1 k

 

(36)

k

2

2

 

 

 

h

0

 

 

2 k

 

Эта нелинейная функция от переменной K имеет максимум. Для отыскания вели-

чины K для R max

 

проведём дифференцирование выражения (36) по K и приравняем

производную нулю:

 

 

 

 

 

 

 

 

 

 

 

200
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности