
V. Коэффициент интенсивности напряжений (кин).
1. Поля напряжений и перемещений в окрестности вершины трещины.
2. Частные случаи определения КИН.
3. Численные методы определения КИН.
4. Определение НДС в вершине трещины для анизотропного случая.
-
Поля напряжений и перемещений в окрестности вершины трещины.
 Ставится
задача вычисления напряженно-деформированного
состояния вблизи вершины трещины. Данная
задача сводится к решению плоской задачи
теории упругости для математического
разреза с граничными условиями,
реализующими один из типов трещин.
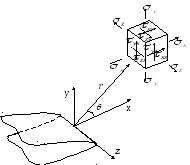
Рассмотрим тело с трещиной (Рис. 1),
выберем систему координат с центром в
вершине трещины.
Ставится
задача вычисления напряженно-деформированного
состояния вблизи вершины трещины. Данная
задача сводится к решению плоской задачи
теории упругости для математического
разреза с граничными условиями,
реализующими один из типов трещин.
Рассмотрим тело с трещиной (Рис. 1),
выберем систему координат с центром в
вершине трещины.
Рис. 1. – Тело с трещиной.
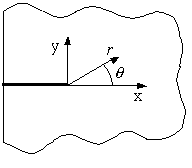
Заменим реальную трещину математическим разрезом (Рис. 2), решение задачи удобно рассматривать в полярных координатах (центр координат в вершине трещины).
![]()
Рис. 2. – Математическая модель тела с трещиной.
Аналитические решения могут быть получены с помощью методов функций комплексного переменного. Решение в явном виде задачи теории упругости по определению напряженно-деформированного состояния вблизи вершины трещины существует для трех типов простых трещин. В полученных решениях для перехода от плоского-напряженного состояния к плоско-деформированному состоянию нужно сделать замену:
![]() (5.1)
(5.1)
-
Для трещины нормального отрыва (тип I) решение имеет следующий вид:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
, ![]() ;
(5.2)
;
(5.2)
![]() ;
;
![]() .
.
-
Для трещины поперечного сдвига (тип II):
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
(5.3)
;
(5.3)
![]() ;
;
![]() .
.
-
Для трещины продольного сдвига ( тип III ):
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
(5.4)
;
(5.4)
![]() .
.
![]() ,
,
![]() ,
,
![]() – величины, характеризующие изменение
напряженно-деформированного состояния
в вершине трещины, зависящие от геометрии
образца и внешних нагрузок, называются
коэффициентом интенсивности напряжений
соответственно для трещины нормального
отрыва (I тип),
поперечного (II
тип) и продольного (III
тип) сдвига.
– величины, характеризующие изменение
напряженно-деформированного состояния
в вершине трещины, зависящие от геометрии
образца и внешних нагрузок, называются
коэффициентом интенсивности напряжений
соответственно для трещины нормального
отрыва (I тип),
поперечного (II
тип) и продольного (III
тип) сдвига.
При радиусе,
стремящемся к нулю, ненулевые компоненты
тензора напряжений стремятся к
бесконечности
![]() .
Это является следствием решения задачи
в упругой постановке. Поля напряжений
и деформаций вблизи трещины для каждого
вида трещины отличаются только на
величину КИН (коэффициент интенсивности
напряжений).
.
Это является следствием решения задачи
в упругой постановке. Поля напряжений
и деформаций вблизи трещины для каждого
вида трещины отличаются только на
величину КИН (коэффициент интенсивности
напряжений).
-
Частные случаи определения кин.
Задача определения КИН с математической точки зрения не менее сложная, чем задача определения НДС. В настоящее время имеются только несколько аналитических решений для наиболее простых видов трещин (см. справочники по механике разрушений). Остальные частные случаи получены с помощью различных приближенных методов. Рассмотрим несколько частных случаев, конфигурации которых наиболее часто встречаются в технике и широко используются в инженерных расчетах.
I.Трещина
нормального отрыва в бесконечной
плоскости нагруженная на бесконечности
растягивающим усилием
![]() (Рис. 3, А).
(Рис. 3, А).
![]() (5.5)
(5.5)
Формула (5.5) носит название – «решение Ирвина».
Если образец имеет
ограничения по внешним размерам, то
вводят поправку –
![]() ,
которая называется “К-тарировка”-
коэффициент учитывающий форму, внешние
размеры образца и характер расположения
трещины:
,
которая называется “К-тарировка”-
коэффициент учитывающий форму, внешние
размеры образца и характер расположения
трещины:
![]() (5.6)
(5.6)
II. Краевая трещина в полубесконечной плоскости (Рис.3, Б):
![]() (5.7) формула (5.7) –
«решение Бови».
(5.7) формула (5.7) –
«решение Бови».
-
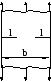
Краевая трещина в бесконечной полосе (Рис. 3, В):
![]() ,
где (5.8)
,
где (5.8)
![]() ,
, ![]() ,
(5.9)
,
(5.9)
здесь b – ширина полосы, l – длина трещины. Формула (5.8) – «решение Гросса».
В реальных задачах
полоса имеет конечные размеры. Если
![]() ,
то используем «решение Гросса»; иначе
необходимо учитывать величину
,
то используем «решение Гросса»; иначе
необходимо учитывать величину
![]() (длину
полосы).
(длину
полосы).
-
Центральная трещина в бесконечной полосе (Рис. 3, Г):
![]() (5.10)
(5.10)
формула (5.10) с учетом условия (5.9) носит название «решения Ирвина».
![]() ,
, ![]()
![]() ,
, ![]() (5.11)
(5.11)
формулы (5.11) –«решение Федерсена».
![]() ,
, ![]() (5.12)
(5.12)
формула (5.12) – «решение Исиды».

А Б В Г
Рис. 3. – Виды трещин:
А) Трещина нормального отрыва;
Б) Краевая трещина в полубесконечной плоскости;
В) Краевая трещина в бесконечной полосе;
Г) Центральная трещина в бесконечной полосе.
V. Бесконечная полоса с двумя краевыми трещинами (Рис. 4, А):
![]() – «решение Бови».
(5.13)
– «решение Бови».
(5.13)
![]() –
«решение Ирвина».
(5.14)
–
«решение Ирвина».
(5.14)
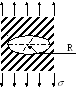
VI. Круглая трещина в массиве (Рис. 4, Б):
![]() ,
(5.15)
,
(5.15)
где
![]() - радиус трещины. Формула (5.15) – «решение
Снеддона».
- радиус трещины. Формула (5.15) – «решение
Снеддона».
VII. Бесконечная плоскость с трещиной поперечного сдвига (Рис. 4, В):
![]() .
(5.16)
.
(5.16)
VIII. Бесконечная плоскость с трещиной продольного сдвига, нагрузка перпендикулярна листу (Рис. 4, Г):
![]() .
(5.17)
.
(5.17)
 А
Б
А
Б




2l


В Г
Рис. 4. – Виды трещин:
А) Бесконечная полоса с двумя краевыми трещинами;
Б) Круглая трещина в массиве;
В) Бесконечная плоскость с трещиной продольного сдвига;
Г) Бесконечная плоскость с трещиной поперечного сдвига.
IX. Трещина в бесконечной анизотропной плоскости (Рис. 5, А):
![]() ;
;
![]() ;
(5.18)
;
(5.18)
![]() .
.
X. Асимметричное расклинивающее усилие в плоскости под произвольным углом (Рис. 5, Б). Суперпозиция трех видов трещин.
![]() ;
;
![]() ;
(5.19)
;
(5.19)
![]() ,
,
где
![]() -
расстояние от оси симметрии до точки,
в которой сосредоточено произвольное
усилие.
-
расстояние от оси симметрии до точки,
в которой сосредоточено произвольное
усилие.

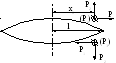
а б
Рис. 5. – Виды трещин:
А) Трещина в бесконечной анизотропной плоскости;
Б) Плоская трещина с произвольным усилием, сосредоточенным на берегах трещины.
Задача определения НДС в простейшем случае сводится к следующему: из справочника берется частное решение наиболее близкое к реальному, из него находится КИН, а затем найденное значение подставляем в асимптотические формулы (5.2 – 5.4).
