- •Федеральное агентство морского и речного транспорта
- •Глава 1. Дискретные случайные Величины
- •1.1. Понятие случайной величины
- •1.2. Функция распределения случайной величины
- •1.3. Закон распределения дискретной случайной величины
- •1.4. Функция распределения дискретной случайной величины
- •1.5. Математическое ожидание дискретной случайной величины
- •1.6. Свойства математического ожидания.
- •3. Теорема сложения для математического ожидания.
- •4. Теорема умножения для математического ожидания.
- •1.7. Дисперсия дискретной случайной величины
- •1.8. Свойства дисперсии
- •7. Математическое ожидание и дисперсия среднего арифметического.
- •1.9. Биномиальное распределение
- •1.10. Распределение Пуассона
- •Глава 2. НепрерыВные случайные Величины
- •2.1. Плотность непрерывной случайной величины
- •2.2. Особенность непрерывной случайной величины
- •2.3. Вероятностный смысл плотности распределения
- •2.4. Математическое ожидание непрерывной случайной величины
- •I. Наводящее рассуждение.
- •II. Определение математического ожидания.
- •III. Математическое ожидание функции случайного аргумента.
- •IV. Свойства математического ожидания непрерывной случайной величины.
- •2.5. Дисперсия непрерывной случайной величины
- •2.6. Нормальное распределение
- •2.7. Показательное распределение
- •2.8. Равномерное распределение
- •2.9. Преобразование случайных величин
- •I. Линейное преобразование нормального закона.
- •II. Общий случай преобразования случайной величины.
- •2.10. Вероятность попадания в промежуток для нормального распределения.
- •I. Вероятность попадания в произвольный промежуток.
- •II. Вероятность отклонения от математического ожидания.
- •III. Правило «трех сигм».
- •2.11. Корреляция случайных величин
- •1. Нормированные случайные величины.
- •2. Корреляционный момент.
- •3. Коэффициент корреляции.
- •Глава 3. Закон больших чисел
- •3.1. Первое неравенство Чебышева
- •3.2. Второе неравенство Чебышева
- •3.3. Сходимость по вероятности
- •3.4. Общий закон больших чисел в форме Чебышева.
- •3.5. Частный закон больших чисел в форме Чебышева.
- •3.6. Закон больших чисел в форме я.Бернулли.
- •3.7. Центральная предельная теорема.
- •Глава 4. ДвумеРные случайные Величины
- •4.1. Функция распределения двумерной случайной величины
- •Свойства функции распределения
- •4.2. Дискретные двумерные случайные величины
- •4.3. Непрерывные двумерные случайные величины
- •Вероятностный смысл плотности
- •4.4. Вероятность попадания случайной точки в заданную область
- •4.5. Свойства плотности непрерывной двумерной случайной величины
- •4.6. Условные законы распределения составляющих
- •I. Случай дискретной двумерной случайной величины.
- •II. Случай непрерывной двумерной случайной величины.
- •4.7. Критерии независимости составляющих
- •Список литературы
- •Оглавление
- •Глава I. Дискретные случайные величины………………...3
- •Глава II. Непрерывные случайные величины ………..…22
- •Глава IV. Двумерные случайные величины ……………………..… 51
- •Ястребов Михаил Юрьевич
2.6. Нормальное распределение
Определение:
Непрерывная случайная величина
![]() имеетнормальное
распределение (распределение Гаусса)
с параметрами
имеетнормальное
распределение (распределение Гаусса)
с параметрами
![]() и
и![]() ,
если ее плотность имеет вид:
,
если ее плотность имеет вид:
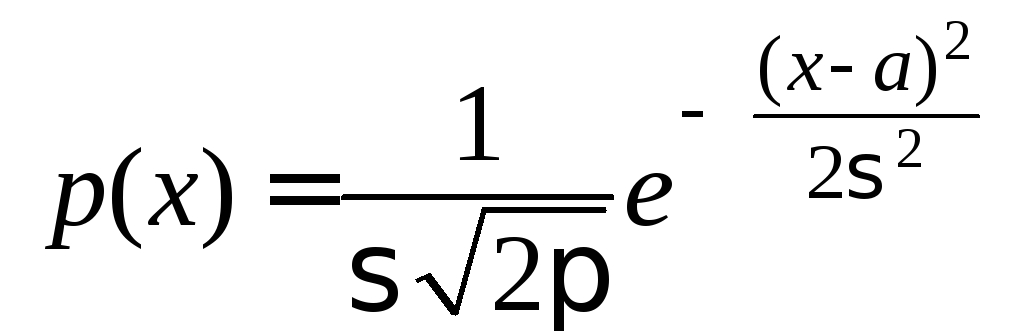 .
(16)
.
(16)
График плотности нормального распределения, изображенный на рис. 4, называется нормальной кривой или кривой Гаусса.
p(x) x a
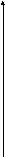

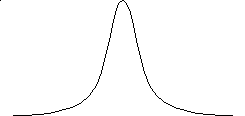

Рис. 4.
Из
графика видно, что из интервалов значений
одинаковой длины более близкие к
![]() имеют большую вероятность, попадание
в них происходит чаще. При удалении от
имеют большую вероятность, попадание
в них происходит чаще. При удалении от![]() вероятность попадания в интервал
уменьшается.
вероятность попадания в интервал
уменьшается.
Такое
поведение вероятностей, а значит, и
относительных частот, характерно для
многих случайных величин. Например,
если
![]() — средний рост, а
— средний рост, а![]() — рост произвольно выбранного человека,
то люди, чей рост близок к среднему,
встречаются часто, а «великаны» и
«карлики» — крайне редко.
— рост произвольно выбранного человека,
то люди, чей рост близок к среднему,
встречаются часто, а «великаны» и
«карлики» — крайне редко.
Замечание.
При
![]() плотность нормального распределения
является дифференциальной функцией
Лапласа [13]:
плотность нормального распределения
является дифференциальной функцией
Лапласа [13]:
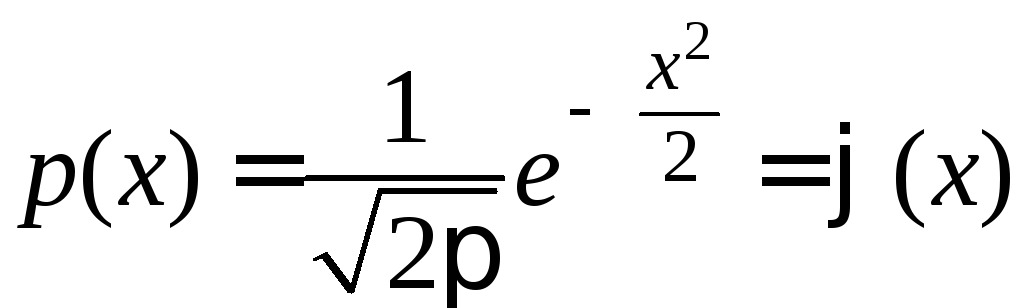 .
.
Функция
распределения
![]() в этом случае задается выражением:
в этом случае задается выражением:
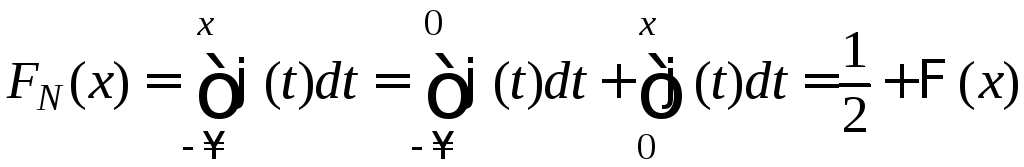 ,
,
где
![]() — интегральная функция Лапласа. Итак,
— интегральная функция Лапласа. Итак,
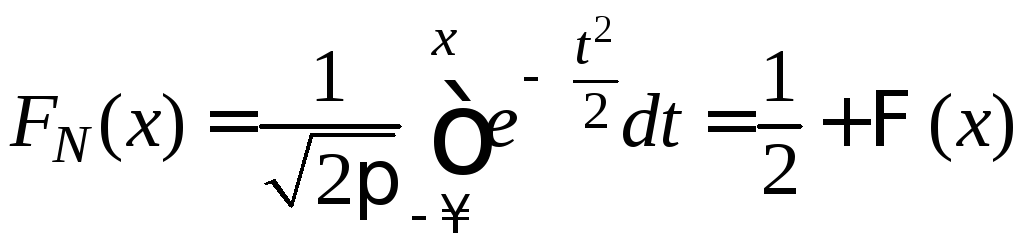 .
.
Зависимость
нормальной кривой от параметра
![]() (при
(при![]() и постоянном
и постоянном![]() )
изображена на рис. 5. Вертикальная прямая
)
изображена на рис. 5. Вертикальная прямая![]() является осью симметрии нормальной
кривой.
является осью симметрии нормальной
кривой.
p(x) x
a1
a2

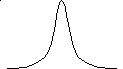



Рис. 5.
Зависимость
нормальной кривой от параметра
![]() (при постоянном
(при постоянном![]() )
изображена на рис. 6. При увеличении
)
изображена на рис. 6. При увеличении![]() кривая становится более пологой, так
что далекие от
кривая становится более пологой, так
что далекие от![]() значения случайной величины
значения случайной величины![]() приобретают большую вероятность,
реализуются чаще; разброс значений
вокруг
приобретают большую вероятность,
реализуются чаще; разброс значений
вокруг![]() при этом увеличивается.
при этом увеличивается.



Рис. 6.
Эти свойства нормальной кривой проясняет
Теорема
(о вероятностном смысле параметров
![]() и
и![]() ).
Для случайной величины
).
Для случайной величины
![]() ,
имеющей нормальное распределение с
параметрами
,
имеющей нормальное распределение с
параметрами![]() и
и![]() :
:![]() .
.
Доказательство.
При вычислении интегралов, выражающих
![]() и
и![]() ,
воспользуемся заменой переменной. В
соответствии с формулой (13):
,
воспользуемся заменой переменной. В
соответствии с формулой (13):
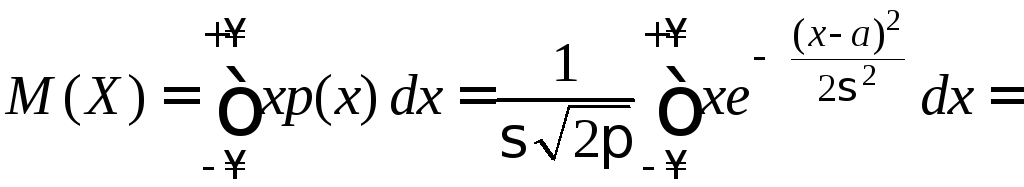
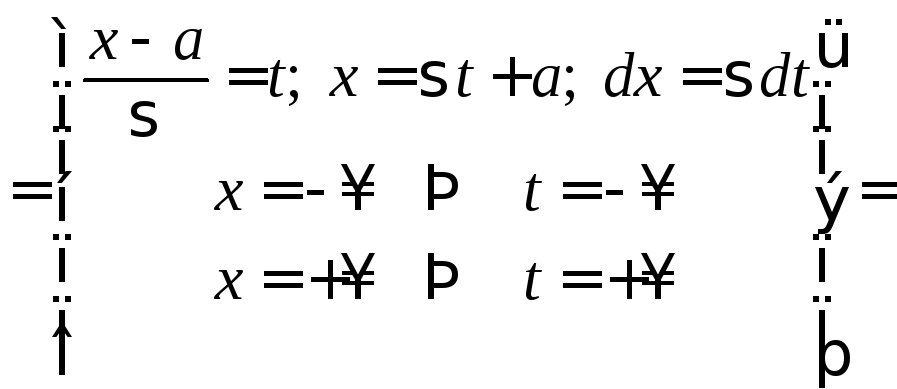
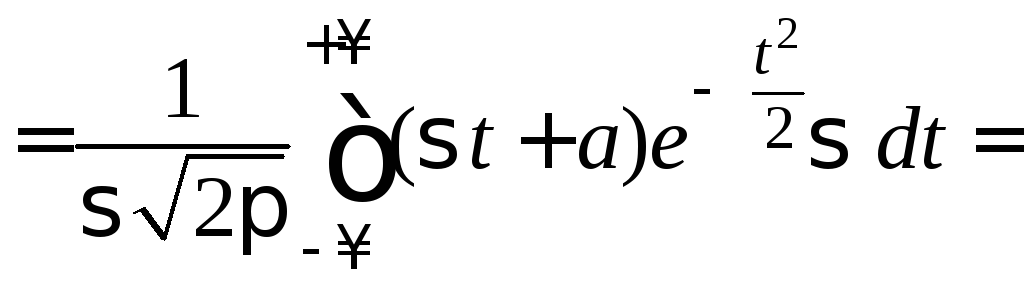
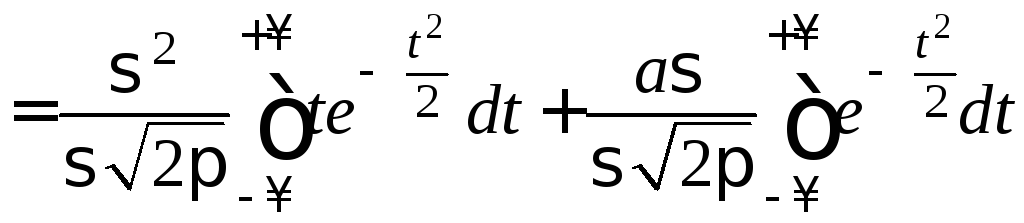 .
.
В
полученном выражении первое слагаемое
является сходящимся интегралом от
нечетной функции
![]() по симметричному промежутку и поэтому
равно нулю. Второе слагаемое представляет
собою умноженный на
по симметричному промежутку и поэтому
равно нулю. Второе слагаемое представляет
собою умноженный на![]() интеграл Пуассона,
про который известно, что он равен
интеграл Пуассона,
про который известно, что он равен
![]() :
:

(в
этом смысл множителя
![]() в формуле для плотности: — он обеспечивает
выполнение равенства (10) ). В результате
получаем:
в формуле для плотности: — он обеспечивает
выполнение равенства (10) ). В результате
получаем:![]() .
.
Аналогичными
вычислениями устанавливается и равенство
![]() .
▄
.
▄
Получим
выражение для функции распределения
![]() произвольного нормального закона с
параметрами
произвольного нормального закона с
параметрами
![]() и
и![]() :
:
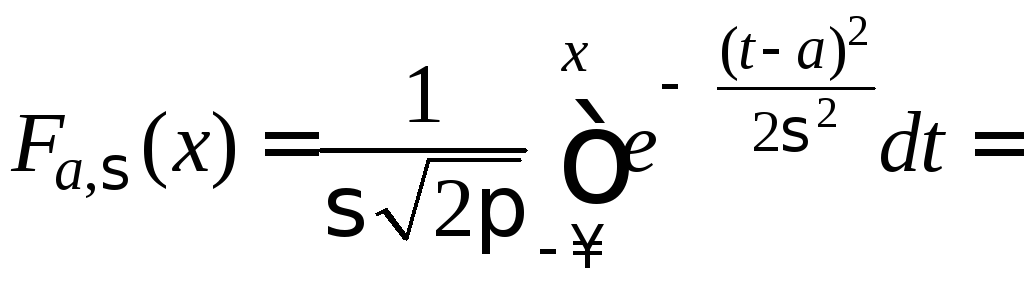
(проводим замену переменной)
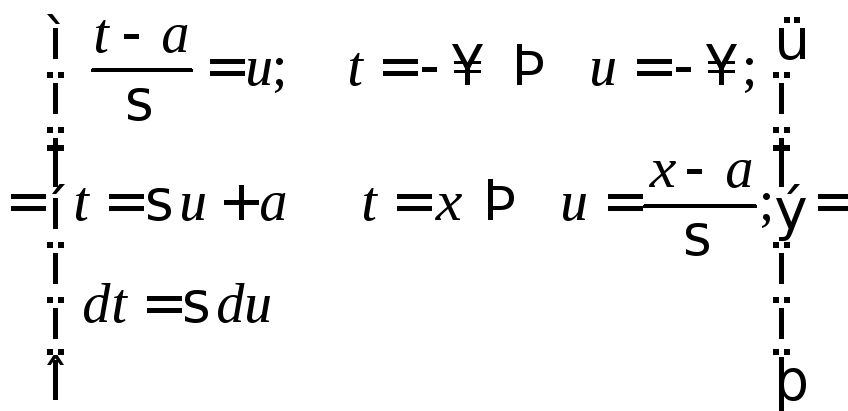
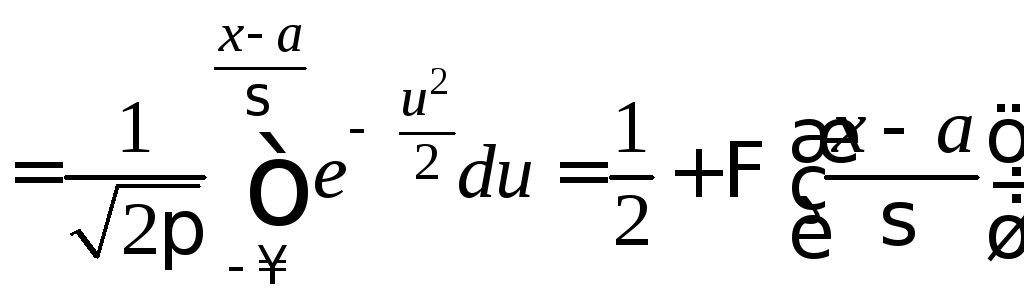 .
.
Нормальное распределение играет исключительно важную роль при математическом описании многих процессов, имеющих вероятностную, случайную (говорят также: — стохастическую — природу).
2.7. Показательное распределение
Определение:
Непрерывная случайная величина
![]() имеетпоказательное
(экспоненциальное)
распределение
с параметром
имеетпоказательное
(экспоненциальное)
распределение
с параметром
![]() ,
если ее плотность имеет вид:
,
если ее плотность имеет вид:
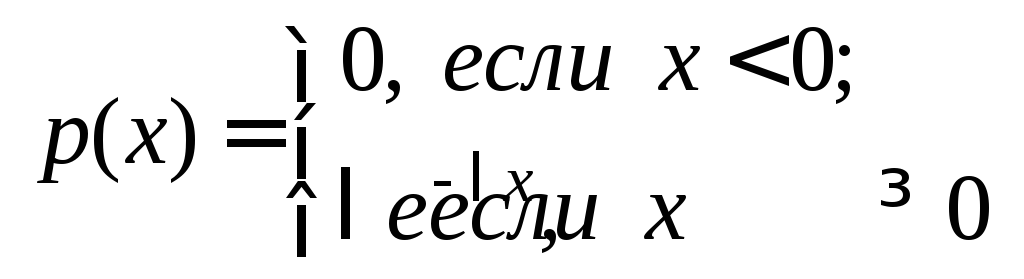 .
(17)
.
(17)
График плотности показательного распределения изображен на рис.7.
Р
 ис.
7.
ис.
7.
Теорема.
Если непрерывная случайная величина
имеет показательное распределение с
параметром
![]() ,
то для ее математического ожидания и
дисперсии справедливы формулы:
,
то для ее математического ожидания и
дисперсии справедливы формулы:
 .
.
Доказательство. Заметим, что по правилу Лопиталя
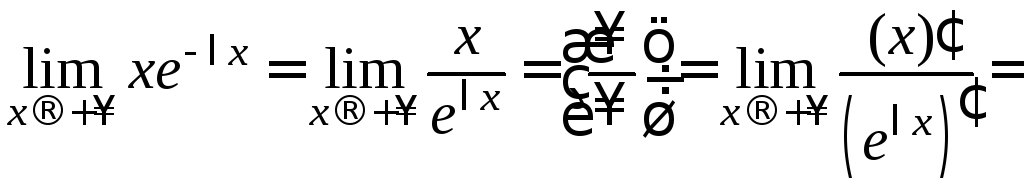
 .
.
Интегрируя по частям, получим:
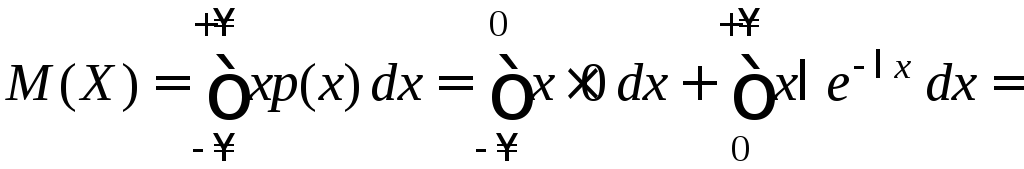
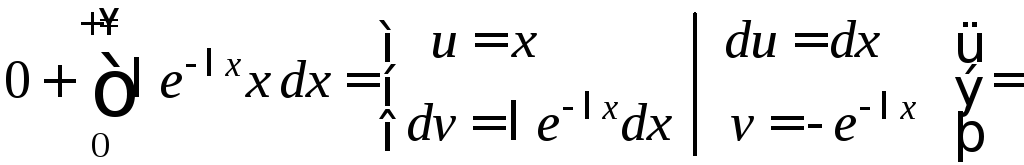

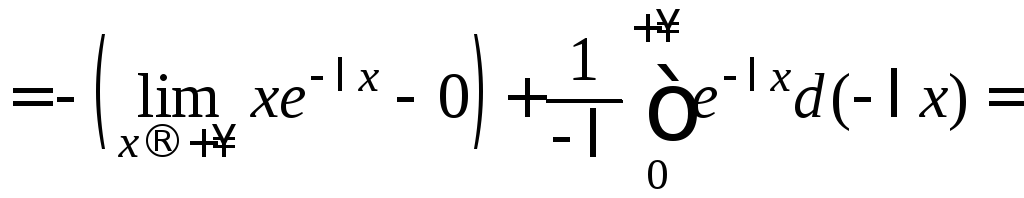
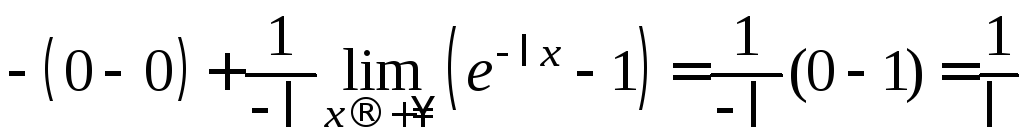 .
.
Далее,
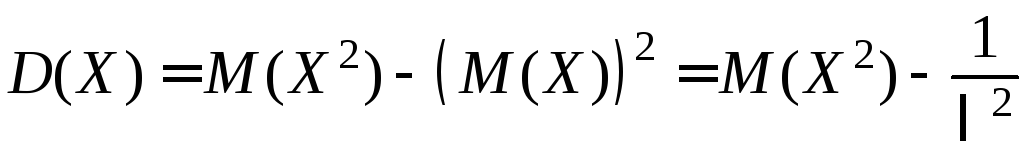 .
.
Согласно формуле (14):
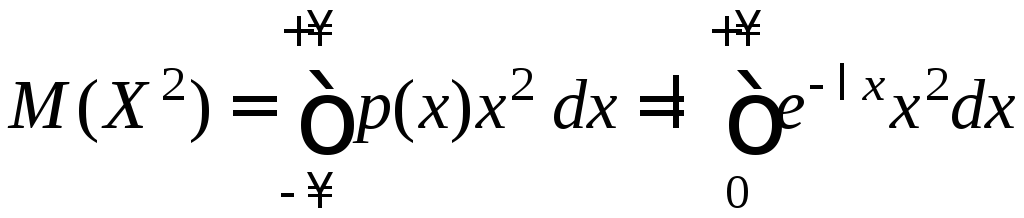 .
.
Аналогично
предыдущему, интегрируя по частям
дважды, получим:
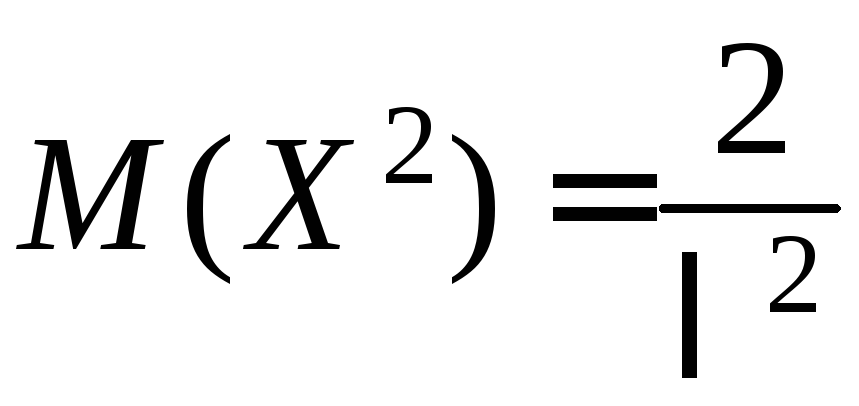 ,
так что
,
так что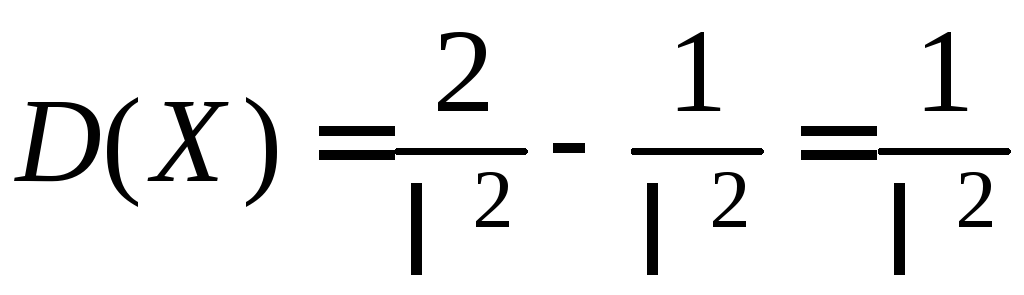 .
▄
.
▄
Аналогичными вычислениями получается выражение для функции распределения показательного распределения: