1.3. Закон распределения дискретной случайной величины

Определение. Случайная величина называется дискретной, если все ее возможные значения можно представить в виде конечной или бесконечной последовательности: .

Определение. Законом распределения дискретной случайной величины называется таблица (конечная или бесконечная), содержащая все ее возможные значенияи вероятности принятия этих значений:

			…		…
			…		…

Будем обозначать закон распределения также в виде:

или .

Примеры. 1. Испытание: бросание игральной кости. Случайная величина — количество выпавших очков. Возможные значения — числа. Для каждого из этих значений схема равновозможных исходов дает вероятность 1/6. Закон распределения имеет вид:

	1	2	3	4	5	6
	1/6	1/6	1/6	1/6	1/6	1/6

2. Испытание: три раза бросается монета. Случайная величина — количество выпадений герба. Возможные значения – числа. Вероятности значений находятся по схеме Бернулли как вероятности числа успехов (см. [13], п. 3.11), где вероятность успеха в отдельном испытании, вероятность неудачи:

;

;

;

.

Закон распределения имеет вид:

	0	1	2	3
	1/8	3/8	3/8	1/8

3. Испытание: Стрельба по мишени до первого попадания. Вероятность попадания при отдельном выстреле равна . Случайная величина— количество произведенных выстрелов. Возможные значения:; множество значений бесконечно. Найдем вероятности этих значений, считая результаты отдельных выстрелов независимыми событиями.

Если первое попадание произошло при -м выстреле, то первыевыстрелов были промахами, а последний,-й, — попаданием. Введем события— попадание при-м выстреле (), так что

.

Тогда по теореме умножения для независимых событий (см. [13], п. 3.8):

.

Теорема. Сумма вероятностей закона распределения дискретной случайной величины равна :

. (1)

(если множество возможных значений бесконечна, то сумма в (1) понимается как сумма ряда, то есть как предел частичных сумм).

Доказательство. События при разных попарно несовместны. Поскольку одно из возможных значений обязательно реализуется в результате испытания, то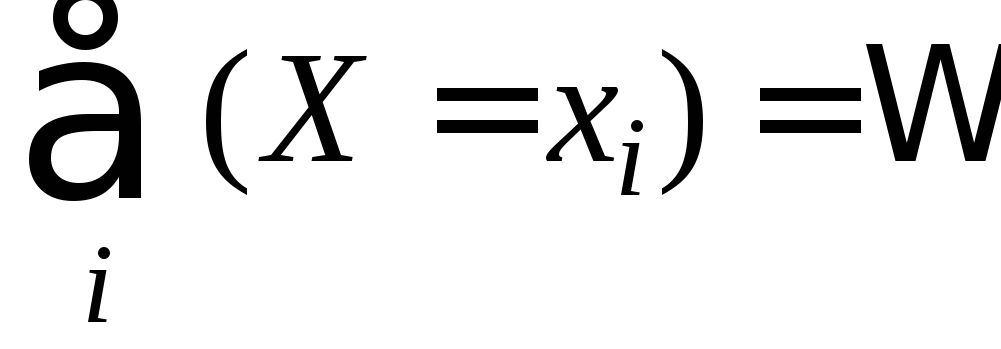. Тогда

. ▄

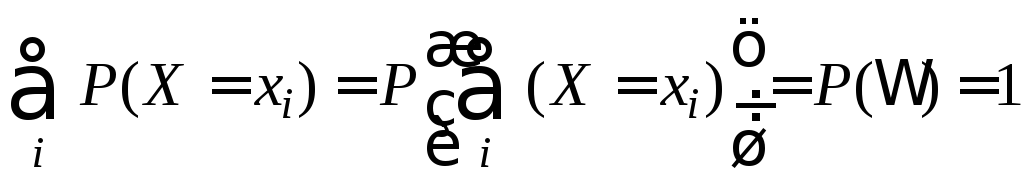1.4. Функция распределения дискретной случайной величины

Рассмотрим задачу нахождения функции распределения дискретной случайной величинына примере следующего закона распределения:

Четыре возможных значения случайной величины разбивают числовую ось на пять промежутков. Рассмотрим поочередно возможные случаи расположения аргумента .

1. Если , то событиеявляется невозможным, в том числе и для крайней точки промежутка. Поэтому.

2. Если , то событиесовпадает с событием, поскольку левееимеется лишь одно возможное значение случайной величины, а именно,. Значит,

.

3. Если , то событиеозначает, чтоили, поскольку левееимеются только два возможных значения случайной величины. Таким образом, имеем для этого случая:— сумма несовместных событий. Значит,

.

4. Если , то событиеозначает, что, или, или, поскольку левееимеются три указанных значения. Таким образом, в этом случае:

— сумма попарно несовместных событий. Значит,

.

5. Наконец, при событиеявляется достоверным, поскольку все возможные значения случайной величины лежат левее. Следовательно,

.

Итак, график функции распределения имеет ступенчатый характер (рис. 2). Точка на правом конце каждой «ступеньки» означает, что именно на ней находится точка графика с данной абсциссой. Наоборот, стрелка на левом конце указывает, что крайняя левая точка «выколота». Таким образом, значения функции вблизи слева от аргумента совпадают со значением функции в самой точке, и, значит, имеют место непрерывность слева и разрыв первого рода (скачок) справа.

Рис.2.

График на рис. 2 наглядно иллюстрирует общие свойства функции распределения, описанные в п.1.2.