
- •Федеральное агентство морского и речного транспорта
- •Глава 1. Дискретные случайные Величины
- •1.1. Понятие случайной величины
- •1.2. Функция распределения случайной величины
- •1.3. Закон распределения дискретной случайной величины
- •1.4. Функция распределения дискретной случайной величины
- •1.5. Математическое ожидание дискретной случайной величины
- •1.6. Свойства математического ожидания.
- •3. Теорема сложения для математического ожидания.
- •4. Теорема умножения для математического ожидания.
- •1.7. Дисперсия дискретной случайной величины
- •1.8. Свойства дисперсии
- •7. Математическое ожидание и дисперсия среднего арифметического.
- •1.9. Биномиальное распределение
- •1.10. Распределение Пуассона
- •Глава 2. НепрерыВные случайные Величины
- •2.1. Плотность непрерывной случайной величины
- •2.2. Особенность непрерывной случайной величины
- •2.3. Вероятностный смысл плотности распределения
- •2.4. Математическое ожидание непрерывной случайной величины
- •I. Наводящее рассуждение.
- •II. Определение математического ожидания.
- •III. Математическое ожидание функции случайного аргумента.
- •IV. Свойства математического ожидания непрерывной случайной величины.
- •2.5. Дисперсия непрерывной случайной величины
- •2.6. Нормальное распределение
- •2.7. Показательное распределение
- •2.8. Равномерное распределение
- •2.9. Преобразование случайных величин
- •I. Линейное преобразование нормального закона.
- •II. Общий случай преобразования случайной величины.
- •2.10. Вероятность попадания в промежуток для нормального распределения.
- •I. Вероятность попадания в произвольный промежуток.
- •II. Вероятность отклонения от математического ожидания.
- •III. Правило «трех сигм».
- •2.11. Корреляция случайных величин
- •1. Нормированные случайные величины.
- •2. Корреляционный момент.
- •3. Коэффициент корреляции.
- •Глава 3. Закон больших чисел
- •3.1. Первое неравенство Чебышева
- •3.2. Второе неравенство Чебышева
- •3.3. Сходимость по вероятности
- •3.4. Общий закон больших чисел в форме Чебышева.
- •3.5. Частный закон больших чисел в форме Чебышева.
- •3.6. Закон больших чисел в форме я.Бернулли.
- •3.7. Центральная предельная теорема.
- •Глава 4. ДвумеРные случайные Величины
- •4.1. Функция распределения двумерной случайной величины
- •Свойства функции распределения
- •4.2. Дискретные двумерные случайные величины
- •4.3. Непрерывные двумерные случайные величины
- •Вероятностный смысл плотности
- •4.4. Вероятность попадания случайной точки в заданную область
- •4.5. Свойства плотности непрерывной двумерной случайной величины
- •4.6. Условные законы распределения составляющих
- •I. Случай дискретной двумерной случайной величины.
- •II. Случай непрерывной двумерной случайной величины.
- •4.7. Критерии независимости составляющих
- •Список литературы
- •Оглавление
- •Глава I. Дискретные случайные величины………………...3
- •Глава II. Непрерывные случайные величины ………..…22
- •Глава IV. Двумерные случайные величины ……………………..… 51
- •Ястребов Михаил Юрьевич
II. Вероятность отклонения от математического ожидания.
Теорема.
Пусть
непрерывная случайная величина
![]() имеет нормальное распределение с
параметрами
имеет нормальное распределение с
параметрами![]() и
и![]() .
Тогда для всякого
.
Тогда для всякого![]() вероятность отклонения значения
вероятность отклонения значения![]() от математического ожидания
от математического ожидания![]() по модулю меньше чем на
по модулю меньше чем на![]() ,
задается формулой:
,
задается формулой:
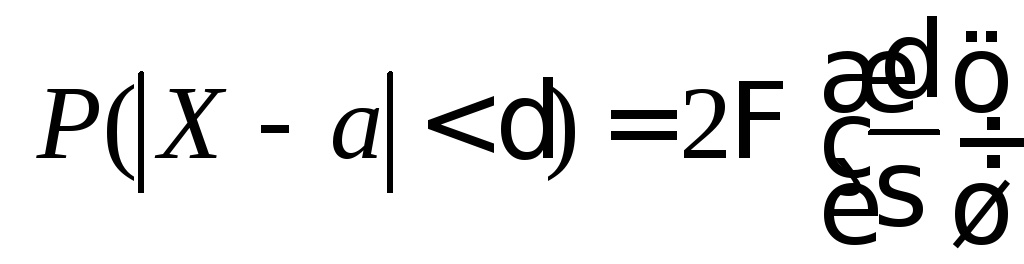 .
(20)
.
(20)
Доказательство. Применим формулу (19) при
![]() ,
так что
,
так что
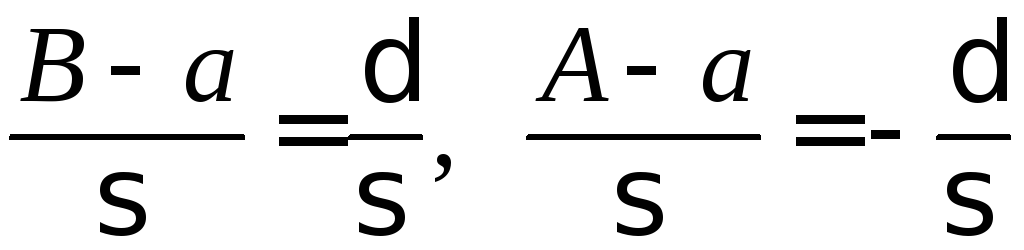 .
Поскольку функция
.
Поскольку функция![]() является нечетной, то
является нечетной, то
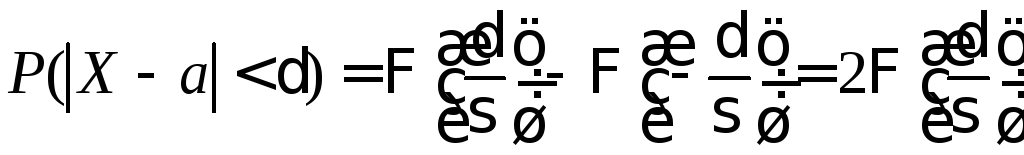 .
▄
.
▄
Пример.
Пусть
![]() имеет нормальное распределение, и
имеет нормальное распределение, и![]() .
Найдем при
.
Найдем при![]() вероятность отклонения от математического
ожидания:
вероятность отклонения от математического
ожидания:
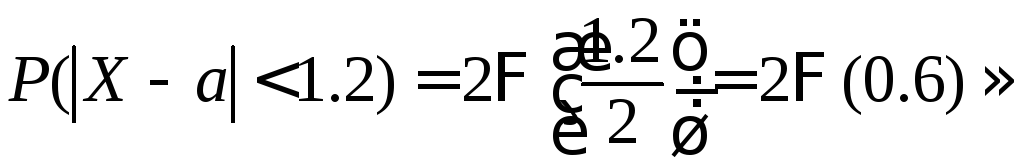
![]() .
.
III. Правило «трех сигм».
Применим
последнюю теорему и формулу (20) к
отклонению
![]() .
При этом
.
При этом
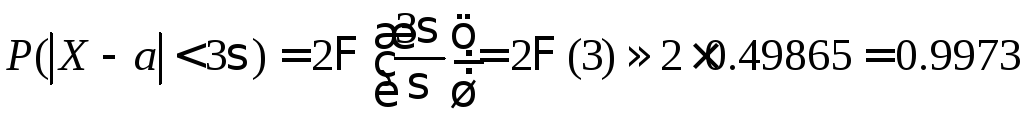 .
.
Итак,
для нормально распределенной случайной
величины с параметрами
![]() и
и![]() вероятность отклонения реализованного
значения от математического ожидания
менее чем на
вероятность отклонения реализованного
значения от математического ожидания
менее чем на![]() ,
приближенно равна
,
приближенно равна![]() .
Во многих
практических ситуациях случайное
событие с такой вероятностью принято
считать практически
достоверным.
.
Во многих
практических ситуациях случайное
событие с такой вероятностью принято
считать практически
достоверным.
Поэтому
полагают, что практически
все реализуемые значения нормально
распределенной случайной величины с
параметрами
![]() и
и![]() попадают в интервал
попадают в интервал![]() .
В этом и заключается «правило трех
сигм».
.
В этом и заключается «правило трех
сигм».
2.11. Корреляция случайных величин
1. Нормированные случайные величины.
Определение.
Случайная
величина
![]() называетсяцентрированной,
если она имеет математическое ожидание,
равное нулю:
называетсяцентрированной,
если она имеет математическое ожидание,
равное нулю:
![]() .
.
Пример.
Случайная величина
![]() ,
распределенная по нормальному закону
с параметрами
,
распределенная по нормальному закону
с параметрами![]() и
и![]() ,
является центрированной, поскольку
,
является центрированной, поскольку![]() .
.
Напомним, что для
случайной величины
![]() ,
имеющей математическое ожидание
,
имеющей математическое ожидание![]() ,
случайная величина
,
случайная величина![]() называетсяотклонением
(отклонением
называетсяотклонением
(отклонением
![]() от математического ожидания).
от математического ожидания).
Теорема.
Отклонение
![]() является центрированной случайной
величиной.
является центрированной случайной
величиной.
Доказательство. По свойствам математического ожидания:
![]() .
▄
.
▄
Определение.
Случайная
величина
![]() называетсянормированной,
если она имеет математическое ожидание,
равное нулю, и дисперсию, равную единице:
называетсянормированной,
если она имеет математическое ожидание,
равное нулю, и дисперсию, равную единице:
![]() .
.
Теорема.
Для случайной величины
![]() ,
у которой
,
у которой![]() ,
,![]() (так что
(так что![]() — среднеквадратическое отклонение),
случайная величина
— среднеквадратическое отклонение),
случайная величина
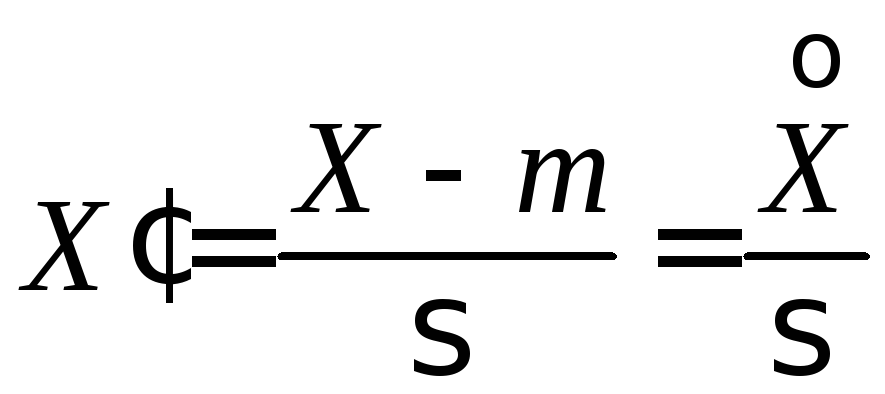 (21)
(21)
является нормированной.
Доказательство. По свойствам математического ожидания и дисперсии:
 ;
;
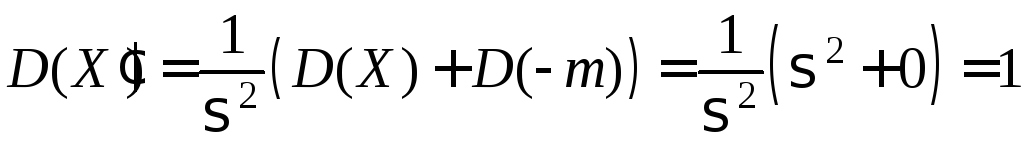 .
▄
.
▄
Теорема.
Для нормированной случайной величины
![]() справедлива
формула:
справедлива
формула:
![]() .
(22)
.
(22)
Доказательство. По формуле разности математических ожиданий (7):
![]() .
▄
.
▄
2. Корреляционный момент.
Определение.
Пусть случайные величины
![]() и
и![]() имеют математические ожидания
имеют математические ожидания![]() и
и![]() .
Их корреляционным моментом
.
Их корреляционным моментом![]() называется математическое ожидание
произведения отклонений:
называется математическое ожидание
произведения отклонений:
![]() .
.
Определение.
1.
Случайные величины
![]() и
и![]() называютсякоррелированными,
если их корреляционный момент не равен
нулю:
называютсякоррелированными,
если их корреляционный момент не равен
нулю:
![]() .
.
2.
Случайные величины
![]() и
и![]() называютсянекоррелированными,
если их корреляционный момент равен
нулю:
называютсянекоррелированными,
если их корреляционный момент равен
нулю:
![]() .
.
Теорема.
Если случайные величины
![]() и
и![]() независимы, то их корреляционный момент
равен нулю:
независимы, то их корреляционный момент
равен нулю:![]() .
.
Доказательство. По свойствам математического ожидания:
![]()
![]()
![]()
![]()
(последнее равенство имеет место по теореме умножения для математических ожиданий независимых случайных величин). ▄
Следствие.
Если случайные величины
![]() и
и![]() являются коррелированными, то они
зависимы.
являются коррелированными, то они
зависимы.
3. Коэффициент корреляции.
Определение.
Коэффициентом
корреляции
случайных величин
![]() и
и![]() ,
имеющих корреляционный момент
,
имеющих корреляционный момент![]() и средние квадратические отклонения
и средние квадратические отклонения![]() ,
называется число
,
называется число
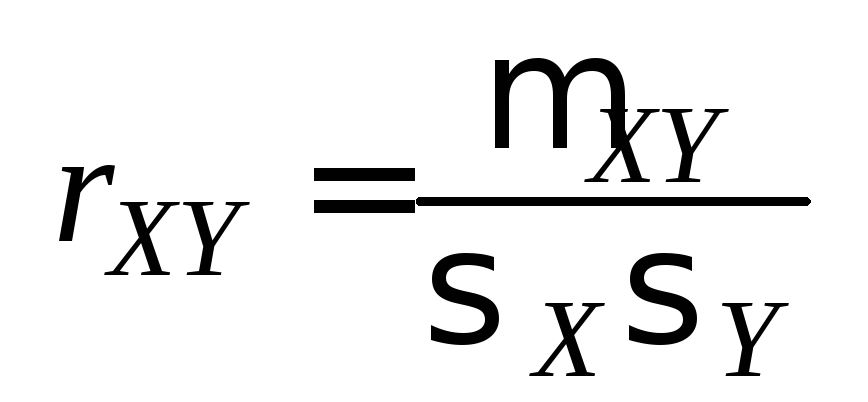 .
.
В
то время как корреляционный момент
![]() является размерной величиной, значение
которой зависит от выбора единиц
измерения
является размерной величиной, значение
которой зависит от выбора единиц
измерения![]() и
и![]() ,
коэффициент корреляции
,
коэффициент корреляции![]() является безразмерной величиной.
является безразмерной величиной.
Теорема (об оценке коэффициента корреляции). Справедливо неравенство:
 .
.
Доказательство.
Пусть
![]() и
и![]() – соответствующие нормированные
случайные величины, полученные по
формуле (21). Тогда, внося постоянные
множители под знак математического
ожидания, имеем:
– соответствующие нормированные
случайные величины, полученные по
формуле (21). Тогда, внося постоянные
множители под знак математического
ожидания, имеем:
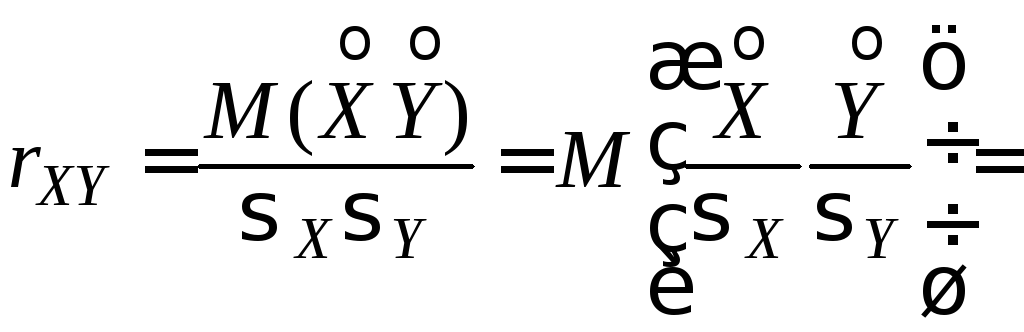
![]() .
(23)
.
(23)
Применим к дисперсии формулу разности математических ожиданий (7):
![]()
![]()
(применим формулу (22) к первому и третьему слагаемым, формулу (23) — ко второму)
![]() .
.
Итак,
![]() .
▄
.
▄
Замечание. В ходе доказательства для нормированных случайных величин установлено равенство:
![]() .
(24)
.
(24)
Теорема (необходимое условие независимости). Если
случайные
величины
![]() и
и![]() независимы, то
независимы, то![]() .
.
Доказательство.
Поскольку
![]() и
и![]() независимы, то
независимы, то
![]() .
▄
.
▄
Теорема
(критерий линейной связи).
Для того чтобы случайные величины
![]() и
и![]() были связаны функциональной линейной
зависимостью вида
были связаны функциональной линейной
зависимостью вида![]() ,
необходимо и достаточно выполнение
условия
,
необходимо и достаточно выполнение
условия![]() .
.
Доказательство.
1. Необходимость. Пусть
![]() ;
по свойствам математического ожидания
и дисперсии:
;
по свойствам математического ожидания
и дисперсии:
![]() ;
;
![]()
![]() .
.
Теперь
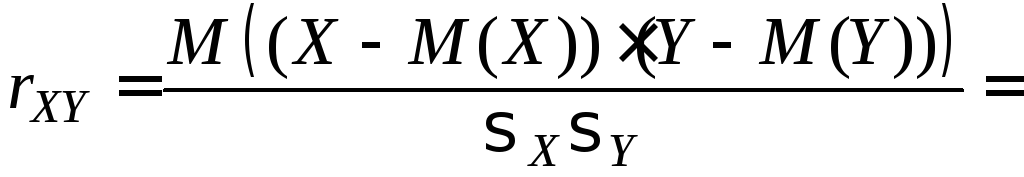
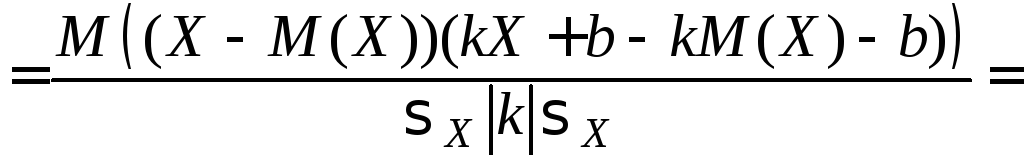
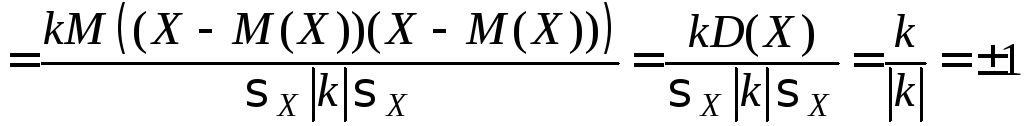 .
.
2.
Достаточность. Пусть
![]() ,
то есть
,
то есть![]() .
Если, например,
.
Если, например,![]() ,
то с учетом (24):
,
то с учетом (24):
![]() ,
,
так
что
![]() .
Тогда, по свойству дисперсии
.
Тогда, по свойству дисперсии
![]() ,
то есть
,
то есть
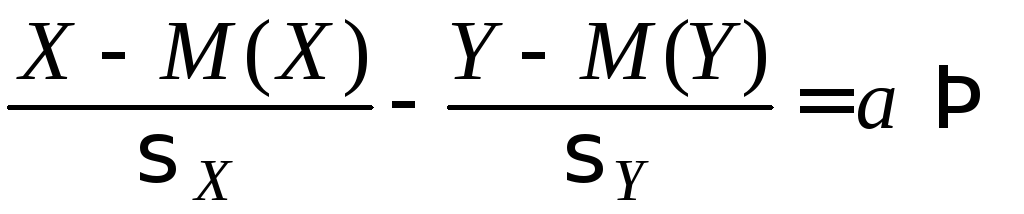
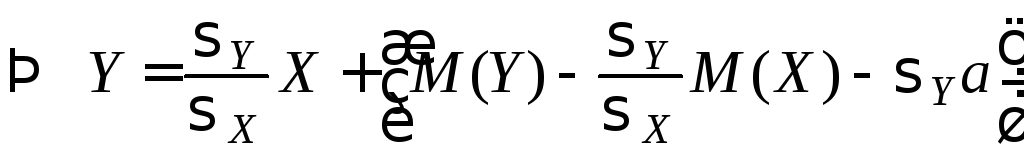 .
.
Остается положить
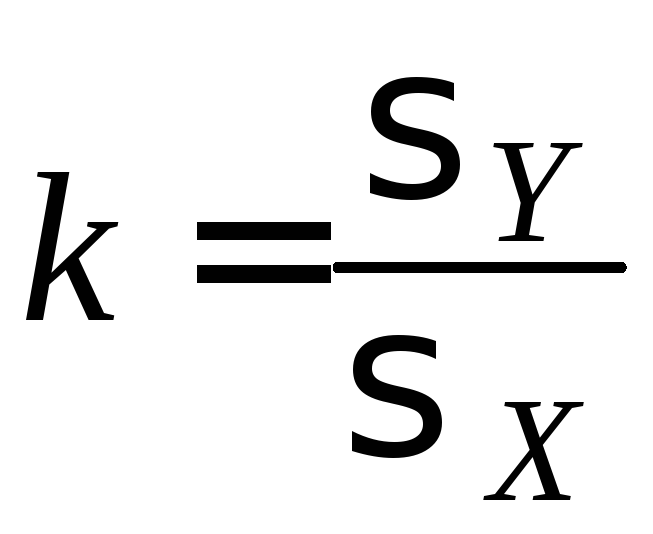 ;
;
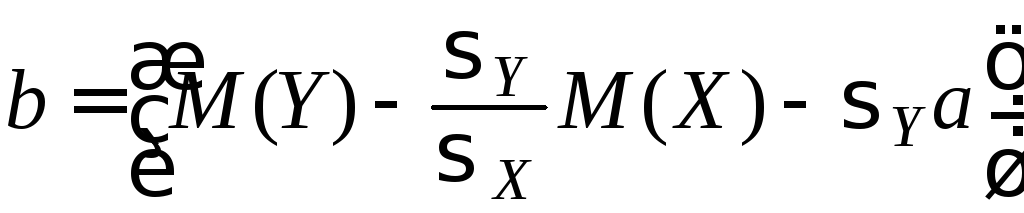 .
▄
.
▄
