
Электроника учебное пособие
.pdfформа, величина и положение во времени. К случайным сигналам относятся сигналы, значения которых заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы.
3. Аналоговые, дискретные и цифровые сигналы.
Сигналы, значения которых можно измерять в произвольные моменты времени, называются аналоговыми.
Дискретным называется сигнал, значения которого определяются в строго заданные моменты времени. Простейшая математическая модель дискретного сигнала Sд (t) – это счетное множество точек {ti} (i – целое
число) на оси времени, в каждой из которых определено отсчетное значение сигнала Si.
Особой разновидностью дискретных сигналов являются цифровые сигналы. Для них характерно, что отсчетные значения представлены в форме чисел. Обычно используют двоичные числа.
4. Периодические и непериодические.
Периодическим называется любой сигнал, для которого выполняется условие
s(t) = s(t + kT ) ,
где период T является конечным отрезком, а k – любое целое число. Простейшим периодическим детерминированным сигналом можно
назвать гармоническое колебание (ток, напряжение), определяемое законом:
s(t) = Acos(2πt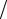 T + θ) = Acos(ωt + θ), − ∞ < t < ∞ ,
T + θ) = Acos(ωt + θ), − ∞ < t < ∞ ,
где А, Т, ω и θ – постоянные амплитуда, период, угловая частота и начальная фаза колебания соответственно.
Непериодическим детерминированным сигналом называется любой детерминированный сигнал, для которого не выполняется условие:s(t) = s(t + kT ) . Примером непериодического сигнала может служить импульсный сигнал.
Импульсные сигналы – это такие сигналы, длительность которых соизмерима с длительностью переходного процесса (колебания, существующие лишь в пределах конечного отрезка времени). Импульсы обладают
41
|
|
B |
|
|
C |
|
B |
|
C |
разнообразной формой. |
Наиболее |
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
распространенные идеализированные |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
A |
|
|
D |
|
|
A |
|
|
|
D |
импульсы приведены на рис. 6.1. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Принято различать следующие участ- |
|||||
прямоугольный |
трапецеидальный |
||||||||||||||||||
|
|
|
B, C |
|
|
|
|
|
|
|
|
ки импульса: AB – фронт, |
BC – |
вер- |
|||||
|
|
|
|
|
|
|
|
|
|
|
шина, срез – CD и основание – AD. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
A |
|
|
D |
|
|
|
|
|
|
|
|
|
Фронт соответствует быстрому |
воз- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
растанию |
сигнала; вершина – |
мед- |
|||||
|
треугольный |
пилообразный |
|||||||||||||||||
|
ленному ее изменению; срез – быст- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рому убыванию сигнала. Иногда срез |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называют задним фронтом в отличие |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
от переднего фронта. |
|
|
||
колоколообразный |
с exp фронтом |
|
|
||||||||||||||||
Рассмотрим идеализированный, |
|||||||||||||||||||
|
и срезом |
||||||||||||||||||
Рис. 6.1. Идеализированные импульсы |
но более сложный по форме импульс |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 6.2). |
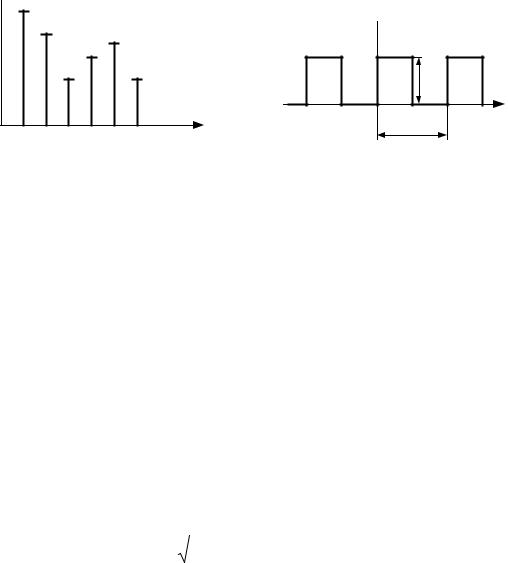
Участок импульса, |
соот- |
||
ветствующий отрицательному напряжению, называют хвостом импульса или обратным выбросом.
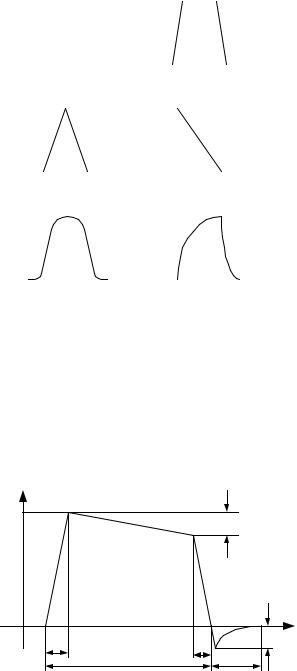
Для величин, указанных на рисунке, обычно используют следующие названия:
|
u |
|
|
|
|
tи – длительность импульса; |
|||
Um |
|
|
|
|
tф – длительность фронта импульса; |
||||
|
|
|
U |
|
|||||
|
|
|
|
|
tс – длительность среза импульса; |
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
tх – длительность хвоста импульса; |
|||
|
|
|
|
|
t |
Um – амплитуда импульса; |
|||
|
tф |
|
|
|
U – спад вершины импульса; |
||||
0 |
tи |
tс |
|
Uобр |
|||||
t |
Uобр – амплитуда обратного вы- |
||||||||
|
|
|
|
х |
|
броса. |
|
|
|
Рис. 6.2. Определение параметров идеали- |
|
|
|||||||
При |
определении |
парамет- |
|||||||
зированного импульса |
|
|
|
||||||
|
|
|
|
|
|
ров реальных импульсов |
обычно |
||
нет возможности однозначно разделить импульс на характерные участки, |
|||||||||
поэтому в этих случаях параметры импульсов определяют, исходя из тех |
|||||||||
или иных соглашений (рис. 6.3). |
|
|
|
|
|||||
42
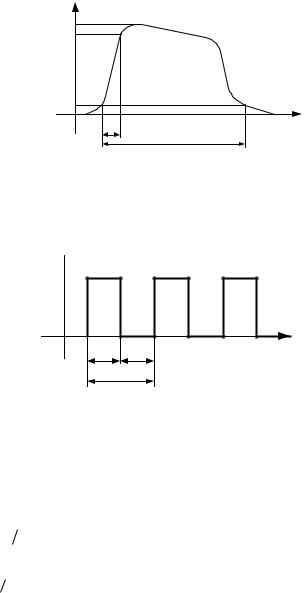
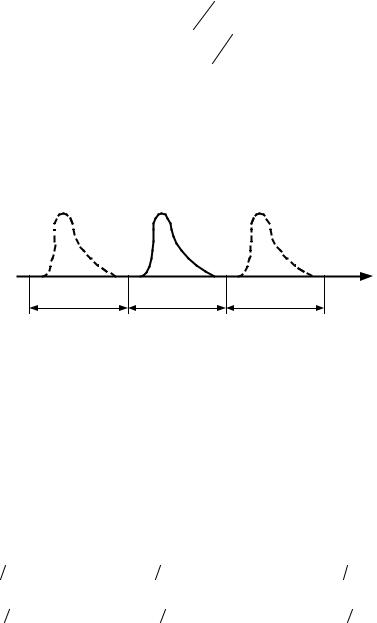
Для периодически повторяющихся импульсов дополнительно используются следующие параметры (рис.6.4):
T – период повторения импульсов;
f = 1 / T – частота повторения импульсов;
tп – длительность паузы;
Q = T / tи – скважность импульсов; K = 1/Q = tи / T – коэффициент за-
полнения.
Во многих практических случаях нарастание и срез импульса происходят по экспоненциальному закону или закону, который может быть аппроксимирован экспонентой. В этом случае анализ импульсных цепей существенно упрощается, так как мгновенные значения импульса во время его нарастания и среза описываются выражениями (6.1) и (6.2) соответственно
Um |
u |
|
|
|
|
|
|
||
0.9Um |
|
|
|
|
0.1Um |
t |
|
t |
|
0 |
ф |
|||
|
tи |
Рис. 6.3. Определение параметров реального импульса
u
0 |
tи |
tп |
t |
|
|
Т |
|
Рис. 6.4. Определение параметров последовательности импульсов
u = A (1− e−t τ ); |
(6.1) |
u = Ae−t τ , |
(6.2) |
где τ – постоянная времени нарастания.
Зная мгновенное значение импульса, можно найти время t, в течение которого импульс достиг этого значения: t = −τln(u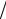 A).
A).
Так как активную длительность фронта (время установления) и среза определяем как промежуток времени между значениями, равными 0,1 и 0,9 А, то
tф = tс = τ[ln(0,9A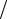 A)− ln(0,1A
A)− ln(0,1A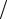 A)]≈ 2,2τ .
A)]≈ 2,2τ .
43

§ 6.2. CПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
Спектры простейших периодических сигналов. Из курса матема-
тики известно, что любая периодическая функция может быть представлена бесконечной суммой ортогональных функций, в качестве которых удобно использовать синус (sin) и косинус (cos). В этом случае периодическое колебание представляется рядом Фурье в следующем виде:
|
|
|
|
|
s(t) = |
a0 |
+ |
∞ |
(a |
|
cos nωt + b sin nωt), |
(6.3) |
|
|
|
|
|
|
å |
n |
|||||
|
|
|
|
|
2 |
|
|
n |
|
|||
|
|
|
|
|
|
n=1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
T 2 |
|
|
|
|
|
||||
где a0 = |
|
ò s(t)dt – постоянная составляющая, |
|
|||||||||
|
T |
|
||||||||||
|
|
−T 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
T 2 |
|
|
|
|
|
||||
an = |
|
ò s(t)cos(nωt)dt |
– амплитуда n-й косинусоидальной состав- |
|||||||||
|
T |
|||||||||||
|
|
−T 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
ляющей; |
|
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
T 2 |
|
|
|
|
|
||||
|
ò |
s(t)sin(nωt)dt |
|
|
|
|
|
|||||
b = |
T |
|
– |
амплитуда n-й синусоидальной |
состав- |
|||||||
|
−T 2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
ляющей колебания.
Итак, в общем случае периодический сигнал содержит независящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами ωn = nω (n = 1, 2, 3, ...), кратными основной частоте.
Каждую гармонику можно описать ее амплитудой An и начальной фазой ϕn. Для этого коэффициенты ряда Фурье следует записать в виде
an = An cos(ϕn ), bn = An sin(ϕn ),
откуда An = 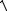
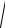 an2 + bn2 , tgϕn = bn
an2 + bn2 , tgϕn = bn 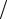 an .
an .
Подставив эти выражения в (6.3), получаем другую эквивалентную форму ряда Фурье:
44
s(t)= |
a0 |
+ |
∞ |
A |
cos(nwt - j |
|
). |
(6.4) |
|
å |
n |
||||||
2 |
|
n |
|
|
|
|||
|
n=1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Совокупность амплитуд гармонических составляющих называется амплитудным спектром колебания. Амплитудный спектр графически представляют в прямоугольной системе координат, откладывая по оси ординат амплитуду, а по оси абсцисс частоту соответствующей гармонической составляющей (рис. 6.5). В случае элементарного гармонического колебания амплитудный спектр представляется единственной составляющей, амплитуда которой равна А, а частота – w или f.
An 
ω 2ω 3ω ... f
 s(t)
s(t)
|
|
|
E |
t |
|
|
|
|
|
Τ |
Τ−τ |
0 |
τ T |
Τ+τ |
Рис. 6.5. Амплитудный спектр |
Рис. 6.6. Периодическое колебание |
гармонического колебания |
прямоугольной формы (меандр) |
Спектр прямоугольного колебания. Подобное колебание называет-
ся меандром (рис. 6.6). Используя формулу (6.3), получаем:
|
|
|
a0 |
|
1 |
τ |
|
|
t |
|
|
|
|
|
||||
|
|
|
|
= |
|
|
ò Edt = |
|
E , |
|
|
|||||||
|
|
2 |
T |
T |
|
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
2 E |
|
|
|
|
|
0τ = |
E |
|
||||||
an = |
ò E cos(nwt) dt = |
|
sin (nwt ) |
|
sin (nwt), |
|||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||
T |
T nw |
np |
||||||||||||||||
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
τ |
2 E |
|
|
0τ = |
E |
(1 - cos(nwt)). |
|||
bn = |
ò E sin (nwt ) dt = |
|
-cos(nwt ) |
||||||||
|
|
|
|
|
|||||||
T |
T nw |
np |
|||||||||
|
0 |
|
|
|
|
||||||
Откуда амплитуда n-й гармоники
|
|
|
|
2E |
æ nwtö |
|
||
A = |
a2 |
+ b2 |
|
|
||||
= |
|
sinç |
|
÷ |
, |
|||
|
|
|||||||
n |
n |
n |
|
np |
è |
2 ø |
|
|
|
|
|
|
|
||||
45
Фаза n-й гармоники
|
|
æ |
bn |
|
j |
n |
= arctgç |
||
|
||||
|
ç |
|
||
|
|
è an |
||
ö |
æ E |
np |
(1- cos(nwt))ö |
|
nwt |
|
||
÷ |
= arctgç |
|
|
÷ |
= |
. |
||
|
|
|
|
|||||
÷ |
ç |
|
E npsin(nwt) |
÷ |
2 |
|
||
ø |
è |
|
ø |
|
||||
Спектральный анализ непериодических сигналов. Гармонический анализ периодических колебаний можно распространить и на непериодические колебания. Пусть такое колебание s(t) задано в виде некоторой функции, отличной от нуля в промежутке [t1, t2] (рис. 6.7).
t
Τ |
0 |
t1 |
Τ |
t |
2 |
Τ |
|
|
|
|
Рис. 6.7. Одиночный сигнал
Выделив произвольный отрезок времени T, включающий в себя промежуток (t1, t2), мы можем представить заданное колебание в виде ряда Фурье в комплексной форме:
∞
s(t) = åcneinωt , 0 < t < T,
n=−∞
где w=2p/T, а коэффициенты сn
|
1 |
T 2 |
|
|
1 |
T 2 |
|
|
|
|
|
|
1 |
T 2 |
|
|
cn = |
ò s(t)e−inωtdt = |
ò |
|
s(t)cos(nwt)dt - i |
ò s(t)sin(nwt)dt . |
|||||||||||
T |
T |
|
T |
|||||||||||||
|
−T 2 |
|
|
−T 2 |
|
|
|
|
|
|
−T 2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∞ |
æt |
2 |
|
|
−inωx |
|
ö |
inωt |
w |
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
|
|
|
|
||||||
|
|
s(t) = å |
ç ò s(x)e |
|
|
dx |
÷e |
|
|
, 0 < t < T. |
(6.5) |
|||||
|
|
|
|
|
2p |
|||||||||||
|
|
n=−∞ è t1 |
|
|
|
|
|
ø |
|
|
|
|
|
|
||
Здесь учтено, что T = 2p/w. Вне отрезка (0, Т) данный ряд определяет периодическую функцию, полученную повторением s(t) вправо и влево с периодом Т. Для того чтобы вне отрезка (0, Т) функция равнялась нулю, величина Т должна быть бесконечно большой. Но чем больше отрезок Т, 46
выбранный в качестве периода, тем меньше коэффициенты сn. Устремляя Т к бесконечности, в пределе получаем бесконечно малые амплитуды гармонических составляющих, сумма которых изображает непериодическую функцию s(t). Число гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, так как при Т ® ¥ основная частота функции w = 2p/T ® 0. Иными словами, расстояние между спектральными линиями, равное основной частоте w, становится бесконечно малым, а спектр – сплошным.
Поэтому в выражении (6.5) можно заменить w на dw, nw на текущую частоту w, а операцию суммирования – операцией интегрирования. Тогда
|
1 |
∞ |
æt2 |
ö |
|
|
s(t) = |
ò |
eiωt ç ò s(x)e−iωxdx ÷ dw. |
(6.6) |
|||
|
||||||
|
2p |
−∞ |
ç t |
÷ |
|
|
|
|
|
è 1 |
ø |
|
|
Внутренний интеграл, являющийся функцией w,
S(w) = tò2 s(t)e−iωt dt
t1
называется спектральной плотностью, или спектральной характеристи-
кой функции s(t). В общем случае, когда t1 и t2 не уточнены, спектральная плотность записывается в форме
|
|
∞ |
|
|
S(w) = ò s(t)e−iωt dt , |
(6.7) |
|||
|
−∞ |
|
||
После подстановки (6.7) в (6.6) |
получаем |
|
||
|
1 |
∞ |
|
|
s(t) = |
ò S(w)eiωt dw. |
(6.8) |
||
2p |
||||
|
−∞ |
|
||
Выражения (6.7) и (6.8) называются соответственно прямым и об-
ратным преобразованиями Фурье.
Контрольные вопросы
1.Перечислите способы классификации электрических сигналов.
2.Чем отличаются дискретные сигналы от цифровых?
47
3.Дайте определение понятия периодического сигнала.
4.Назовите основные параметры импульсных сигналов.
5.Как принято определять длительность импульсных сигналов?
6.Что такое амплитудный спектр периодического сигнала?
7.В чем заключаются прямое и обратное преобразования Фурье?
ГЛАВА 7. УСИЛИТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
В процессе преобразования и обработки информации, заложенной в электрических колебаниях, часто оказывается, что уровень мощности этих колебаний недостаточен для работы потребителя и возникает необходимость в его увеличении. Для этой цели используются электронные усилители.
Усилителем электрических сигналов называется устройство, кото-
рое позволяет при наличии на входе колебаний с некоторым уровнем мощности получить на выходной нагрузке колебания той же формы, но с большим уровнем мощности.
Любой усилитель содержит активный усилительный элемент, ис-
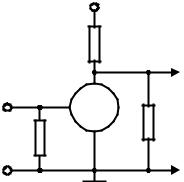
точник питания и пассивные цепи. Усиление происходит за счет того, что активный усилительный элемент, например транзистор, преобразует энергию источника питания в энергию полезных колебаний. Входное колебание является управляющим, так как под его воздействием на выходе усилительного элемента возникают более мощные колебания, передаваемые в
|
Eпит |
нагрузку. |
|
По отношению к усиливаемым коле- |
|
|
R |
|
|
баниям усилитель может рассматриваться |
|
|
|
как электрический четырехполюсник, по- |
|
УЭ |
скольку имеет две входные и две выходные |
Uвх Rвх |
Uвых |
клеммы. Как правило, одна входная и одна |
Rвых |
выходная клеммы эквипотенциальны, так |
|
|
|
|
|
|
как соединены с общей шиной, называемой |
Рис. 7.1. Структура усилителя |
"землей" (рис. 7.1). |
|
|
||
48
Усилители обычно состоят из нескольких однотипных элементарных ячеек, которые называют усилительными каскадами. Усилительный каскад может содержать один, два и более транзисторов, т.е. сам по себе может представлять достаточно сложную схему. Однако каскад, даже сложный, нельзя разделить на более простые компоненты без утраты его специфических свойств. В этом смысле каскад называют элементарной ячейкой уси-
лителя.
§ 7.1. КЛАССИФИКАЦИЯ УСИЛИТЕЛЕЙ. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
Классификацию усилителей можно проводить по различным призна-
кам:
1)по виду используемого усилительного элемента – ламповые, транзисторные усилители, на туннельных или параметрических диодах, на микросхемах и т.д.;
2)по диапазону усиливаемых частот – усилители постоянного тока (УПТ), низкой частоты (УНЧ), радиоили промежуточной частоты (УРЧ, УПЧ) и сверхвысокой частоты (СВЧ-усилители);
3)по ширине полосы усиливаемых частот – узкополосные, широкополосные усилители;
4)по характеру усиливаемого сигнала – усилители непрерывных и импульсных сигналов;
5)по усиливаемой электрической величине – усилители напряжения, тока, мощности;
6)по типу нагрузки – резистивные (апериодические), резонансные (избирательные) усилители.
Работу усилителей принято оценивать рядом показателей и характеристик, которые показывают, как преобразуется входной сигнал в зависимости от параметров усилителя.
Коэффициентом преобразования, или коэффициентом передачи на-
зывают отношение выходного сигнала к входному. S = Iвых / Uвх – коэффициент преобразования напряжения в ток, W = Pвых / Iвх – коэффициент преобразования тока в мощность. В частном случае, когда входное и выходное значения сигнала однородны, коэффициент преобразования называют ко-
49

эффициентом усиления. В качестве величин, характеризующих уровень сигнала, могут использоваться напряжение, ток или мощность.
Коэффициентом усиления по напряжению KU (току KI ) называется
отношение напряжения Um вых (тока |
Im вых ) к входному напряжению |
Um вх (току Im вх ) |
|
KU = Umвых |
Umвх , |
KI = Imвых |
Imвх . |
Из-за наличия в схеме усилителя реактивных элементов (L, C) коэффициенты KU и KI являются комплексными величинами и зависят от частоты усиливаемых сигналов.
Коэффициент усиления по мощности KP показывает, во сколько раз активная мощность Pвых , отдаваемая усилителем в нагрузку, Rн , больше активной мощности Pвх , подводимой к его входным зажимам:
KP = Pвых 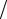 Pвх .
Pвх .
Вряде случаев коэффициенты усиления выражают в логарифмических единицах – децибелах (дБ):
KU = 20lg(Uвых 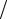 Uвх );
Uвх );
KI = 20lg(Iвых 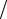 Iвх );
Iвх );
KP = 10lg(Pвых 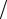 Pвх ).
Pвх ).
Динамическим диапазоном называют отношение наибольшего допустимого значения входного напряжения к его наименьшему допустимому значению:
D = Dвх max 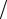 Dвх min ,
Dвх min ,
D(дБ) = 20lg(Dвх max 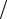 Dвх min ).
Dвх min ).
Введение коэффициента D, характеризующего динамический диапазон, необходимо потому, что максимально допустимое входное напряже-
50
