Зубенко, Омельчук - Програмування. Поглиблений курс

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

Якщо (a,b) R , то кажуть, що елемент a перебуває у відношенні R з елементом b . Цей факт також записують aRb . Образом елемента a

значається як R (X ) = R(x) . Прообразом елемента b за відповідно-

x X

сті R називається сукупність R−1 (b)={a A : (a,b) R}. Прообраз під- множини Y B за відповідності R визначається як

R−1 (Y )= R−1(y) . З відношеннями як множинами можна виконува-

y Y

ти всі згадувані теоретико-множинні операції. Однак існують і спе- цифічні операції. Оберненням відношення R A B називається від-

ношення R−1 ={(b,a ): b B & a A & aRb}. За означенням R−1 B A .

Добутком відношень P A B та Q B C називається відношення

def

P oQ = {(a,c ): b B (a A & c C & aPb & bQc )}.

За означенням P oQ A C . Сама операція o називається множен- ням відношень. Наведемо важливі властивості операції множення:

(P oQ )oR = P o(Q oR ) – асоціативність; R oiB = iA oR = R – діагональ;

(P oQ )−1 = (Q−1 oP −1 ) – обернення добутку.

def

Rn = R o...oR називається n -м степенем відношення R .

1442443

n

Нехай є скороченням фрази "тоді й тільки тоді". Довільне від- ношення R на множині A називається:

1) рефлексивним x A xRx iA R ;

2) симетричним x,y A (xRy → yRx ) R−1 = R ;

3)транзитивним x,y,z A (xRy & yRz → xRz ) RR R ;

4)антисиметричним x,y A (xRy & yRx → x = y) R−1 ∩R I .

Із транзитивністю пов'язане таке важливе поняття, як транзити- вне замикання. Транзитивним замиканням відношення R A A

41

ПРОГРАМУВАННЯ

називається найменше транзитивне відношення R∞ A A , що мі- стить R . Має місце

Лема 1.1. 1) R∞ = U∞ Ri ; 2) R∞ збігається з перетином усіх транзи-

i =1

тивних надвідношень R .

∞

(див. вправу 22). Отже, Ri – найменше транзитивне надвідношен-

i =1

ня R . Далі, перетин усіх транзитивних надвідношень R є транзитив- ним, а враховуючи, що в даному перетині бере участь і найменше з транзитивних надвідношень R , перетин збігається з ним ■

Наприклад, для R ={(n,n +1): n N } транзитивне замикання R∞ збігається зі стандартним числовим порядком <.

1.2.5. ЕКВІВАЛЕНТНОСТІ Й ПОРЯДКИ

Довільні відношення R на множині A називаються:

1) частковим порядком, якщо R є рефлексивним, транзитивним і антисиметричним;

2) лінійним порядком, коли R є частковим порядком таким,

що x,y A (xRy yRx );

3) еквівалентністю, якщо R є рефлексивним, транзитивним і си- метричним.

Частково впорядковану множину будемо називати чумом, або ґра- тами, а її порядок позначати p . Якщо a p b , то кажуть, що елемент a менший ніж b , а елемент b більший ніж a . Якщо при цьому a ≠ b , то кажуть, що a строго менший ніж b , а b – строго більший ніж a .

Елемент a0 чуму А називається найбільшим (найменшим), якщоa A(a p a0 )( a A(a0 p a)). Найбільший і найменший елементи чуму

a A←(a0 p a ) a A←(a p a0 ). Отже, довільний елемент a A або не- порівнянний із максимальним елементом a0 , або менший за нього. Вер-

42

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

хнім (нижнім) конусом підмножини B A називається сукупність усіх таких елементів a A , що b B(b p a) ( b B(a p b) ). Найменший

(найбільший) елемент верхнього (нижнього) конуса підмножини B на- зивається її верхньою (нижньою) гранню й позначається supB ( inf B ).

Чум можна подавати графічно за допомогою діаграм Гессе. У діаг- рамі Гессе елемент y більший за елемент x , якщо в ній існує шлях

від y до x за стрілками, напрямленими вниз. З урахуванням транзи-

тивності не має сенсу зображати всі стрілки між елементами. Розглянемо приклад чуму й діаграму Гессе для нього. Приклад 1.7. Діаграма Гессе.

Нехай множина A = {1,2,3,4,5,6,7}, а відношення порядку x p y означає y % x = 0 , тобто y ділиться на x без залишку. Тут A – рефлек-

сивний чум, але він не є лінійно впорядкованим (прості числа 3 і 5 непорівнянні).

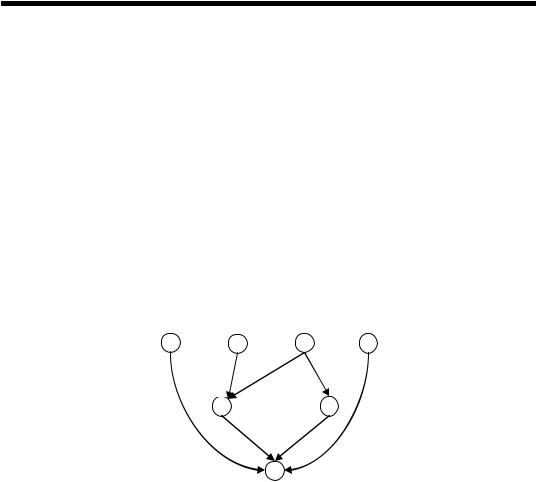
Діаграма Гессе для чуму A має вигляд:

Тут 1 – найменший елемент в A ; 4, 5, 6 i 7 – максимальні. Найбі- льшого елемента в чумі A немає. Верхня грань sup(2, 3)= 6 , нижня –

inf (2, 3)=1, а верхньої грані sup(2, 5) не існує ■

Довільний чум A називається індуктивним, якщо будь-який його зростаючий ланцюг a1 p a2 p ...an p ... має найменшу верхню грань

43

ПРОГРАМУВАННЯ

тонність (див. вправу 25). Найменший елемент в А (якщо він існує)

для i =1,n (див. вправу 28).

Теореми про нерухому точку використовуються при дослідженні й розв'язанні рівнянь і систем рівнянь у різних алгебрах, у тому числі в алгебрах відношень, мов слів тощо.

Чум, в якому для кожних двох елементів існують верхня й нижня грані, називається структурою. Структура називається повною (буле- вою алгеброю), якщо верхня й нижня грані існують для будь-якої її під- множини. Прикладами повної структури є булеві алгебри: а) істиннісних значень {0,1} з операціями диз'юнкції та кон'юнкції (взяття верхньої й

нижньої граней sup та inf , відповідно); б) множини, яку ми розглянули

вище. В останньому прикладі нижню й верхню грані двох і довільної кі- лькості множин задають операції перетину й об'єднання. Не випадково

в літературі часто для довільних чумів терми sup(a,b) та inf (a,b) запи-

сують відповідно a b та a ∩b . Для повних структур виконуються всі закони булевої алгебри множин (див. вправу 24).

Фактор-класами еквівалентності R на A називаються сукупності еквівалентних між собою елементів A . Клас еквівалентності, якому

44

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

належить елемент a , позначається [a]R , або просто [a], для фіксованого R . Сукупність A/R = {[a] : a A} називається фактор-

множиною множини A , а її потужність – індексом R . Процес переходу від довільної множини до її фактор-множини називається факторизацією й відіграє надзвичайно важливу роль у процесах інформаційного моделювання систем.

* Література для CР: множини й відношення – [2, 66, 95, 97, 105, 123]; теорія нерухомої точки – [14, 52, 82, 118, 148].

Контрольні запитання та вправи

1.Дати означення множини.

2.Що таке характеристична й частково характеристична функції?

3.Сформулювати закони булевої алгебри множин.

4.Довести за допомогою діаграм Ейлера – Венна закони 3)–7) булевої алгебри.

5.Довести за допомогою діаграм Ейлера – Венна, що такі три

твердження попарно еквівалентні: а) A B ; б) A ∩ B = A ;

в) A B = B .

6. Спростити вирази:

а) A ∩ B B ;

б) (A ∩ B ∩C ∩ X ) (A ∩C) (B ∩C ) (C ∩ X ),

в)(A ∩ B ∩ X ) (A ∩ B ∩C ∩ X ∩Y ) (A ∩ X ∩ X ) .

7 ** . Нехай A – певна множина. Рівнянням у булевій алгебрі множин B (A)= {2A ; ,∩,\, , } з одним невідомим X називається формула R(A1,...,An ,X ) = (*), де вираз у лівій частині – Ω2 -терм булевої алгебри множин, побудований за допомогою символів операцій алгебри з констант-підмножин A1,...,An A і невідомого X . Наприклад, B C ∩ X = .

З'ясувати, за яких умов рівняння (*) має розв'язок і знайти всі його розв'язки [123].

8.Що таке індексована множина?

9.У чому полягає різниця між сильним і слабким індексуванням?

10.Дати визначення прямої суми множин.

11.Навести приклади застосувань слабкого й сильного індексувань.

12.Чим відрізняються: а) послідовності від підпослідовностей і кортежів; б) кортежі від векторів?

13.Що таке відображення?

45

ПРОГРАМУВАННЯ

14.У чому полягає різниця між відображенням і відповідністю? Проілюструвати прикладами.

15.Яке відношення називається: а) рефлективним; б) симетричним; в) транзитивним; г) антисиметричним; д) частковим порядком; е) лінійним порядком; є) еквівалентністю; ж) структурою, повною структурою? Навести відповідні приклади.

16.Дати означення монотонного й неперервного відображень. Навести відповідні приклади.

17.Що таке нерухома точка відображення?

18.Що таке фактор-множина та індекс еквівалентності?

19.Що таке факторизація множини?

20.Визначимо відношення на словах: u v , якщо слово u є префіксом слова v . Чи буде це відношення: еквівалентністю, лінійним або частковим порядком, структурою на множині всіх слів X * у алфавіті X ?

21.Чи буде сукупність{a,aab,aa,bb,bbc,ab,bbb,d; } чумом?

Якщо так, то побудувати відповідну діаграму Гессе.

22.Нехай R – довільне бінарне відношення. Довести, що будь- яке транзитивне надвідношення R містить Rn , n ≥ 0 .

23.Показати, що булева алгебра множин є повною структурою відносно включення.

24.Довести закони 1)-7) булевої алгебри множин для: а) алгебри істиннісних значень з операціями кон'юнкції та диз'юнкції й запереченням; б) довільної повної структури з нулем і одиницею, доповнення a елемента a в якій визначається системою рівностей a ∩a = 0 та a a =1.

25 * . Показати, що з неперервності відображення випливає його монотонність.

26 * . Показати, що нерухома точка a0 з доведення теореми 1.1 є найменшою. Скористатися монотонністю відображення f .

27.Нехай A – індуктивний чум із нулем ε . Показати, що декар- товий степінь An є індуктивним чумом із нулем (ε,...,ε).

28 * . Довести теорему про нерухому точку для n -арних непере- рвних відображень.

46

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

1.3. Функції як обчислювальні процедури

¾Функціїпроцедури

¾Традиційні способи специфікації функцій

¾Алгебричні специфікації

¾Функції як обчислювальні процедури

Ключові слова: функція-процедура, сюр'єкція, ін'єкція, бієкція, графік функції, композиція рангу 1, композиції множення, розгалуження, обхід, ітерація, повторен- ня, недетермінований вибір, детермінований вибір, регулярна функція, перестанов- ка, ототожнення й параметризація аргументів, введення фіктивних аргументів, підстановка (суперпозиція), ітерації, повторення, регулярна n -арна операція, обчис- лювальний простір, обчислювальна процедура, функція керування, обчислення за процедурою, функція як обчислювальна процедура.

Поняття функції належить до найважливіших понять інформатики. Відомі два різні тлумачення даного поняття: процедурне16 й теоретико-множинне. У першому випадку функція (від лат. functio – виконання, звершення) розглядається як спосіб для отримання певного результату за аргументами, у другому – як синонім теоретико-множинного відображення.

Ці два терміни ввійшли в математичну практику не випадково. Вони мають принципово різний смисловий відтінок. Коли говорять про певне відображення f , то цікавляться тільки тим, чи є пара

Питання про природу цього зв'язку, яким чином він забезпечується, вважається непринциповим. У випадку ж функції-процедури f її

теж розглядають як можливість поставити у відповідність елементам множини A певні елементи множини B , але на перший план виходить спосіб реалізації такого зіставлення при визначенні f

(інтенсіональний підхід).

Процедурний підхід сформувався історично першим (термін запровадив Г. Лейбніц). Однак він був майже витіснений теоретико- множинним на початку ХХ ст. у зв'язку з тотальним переходом

16 Процедура – офіційно встановлений чи узвичайнений порядок здійснення чого- небудь, низка певних цілеспрямованих дій.

47

ПРОГРАМУВАННЯ

математики на нову основу. Достатньо послатись на самі назви сучасних класичних математичних дисциплін – функціональний аналіз, теорія функцій комплексних змінних тощо. Сьогодні процедурний підхід поступово повертає свої позиції завдяки бурхливому розвитку конструктивної математики та інформатики. Поняття функції-процедури є центральним у теорії алгоритмів і програмології, мовах програмування тощо.

Даний підрозділ присвячено функціям як процедурам. Ключовими будуть засоби подання таких функцій.

1.3.1. ФУНКЦІЇ-ПРОЦЕДУРИ

Нехай U – довільна множина.

Функція f – це процедура, яка може бути застосована до одного або кі-

лькох елементів (аргументів) множини U з метою знаходження інших елементів (результату) з U . Застосування функції полягає у проведенні обчислення

– послідовності дій, яке завершується побудовою результату функції.

При цьому функція не завжди гарантує однозначність і навіть іс- нування результату. Це означає, що застосування функції до аргуме- нтів може не привести до результату, а застосування функції повтор- но до тих самих аргументів може приводити до іншого результату. У цьому сенсі всі функції розподіляються на детерміновані й недете- рміновані. Перші гарантують однозначність своїх результатів, усі ре- шта належать до других.

Увага! Надалі нас будуть цікавити в основному детерміновані фу- нкції. Випадки, коли це не так, будуть спеціально зазначатись ►

Існує тісний взаємозв'язок між функціями й алгоритмами. Можна розглядати загальне поняття – функцію та його конкретизацію – алго- ритм. Будь-який алгоритм є функцією-процедурою, а чи буде остання алгоритмом, залежить від способу її визначення. Це обговорювати- меться детально в підрозд. 2.1.4.

Терми f (x ), fx та xf використовуються для запису результату за- стосування функції f до аргументу x . Ураховуючи, що результат та- кого застосування за означенням може бути відсутній, будемо дода- вати до вказаних термів праворуч символ ↓, якщо даний результат

Щоб показати цей зв'язок, функцію f подають у вигляді f : Df → E f

48

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

і називають усюди визначеною на Df . На практиці буває простіше

описати не самі області визначення та значень даної функції, а певні їхні надмножини, наприклад T і R . Щоб підкреслити, що функція f

розглядається над цими загальнішими областями, її записують як f : Т→R і називають частковою, а пару (T ,R ) – типом функції. Будемо вважати вираз f (x ) беззмістовним (тобто рівним # ) для всіх аргуме- нтів поза областю визначеності функції. Графіком функції f назива-

ки функцій використовуються для їх екстенсіонального опису. Функ-

значення Dg функції g є надмножиною області визначення Df фун- кції f (Df Dg ) і виконується умова x Df (fx = gx ), то кажуть, що функція g є еквівалентним накриттям f , або просто накриттям f . В останньому прикладі f є накриттям f0 . Еквівалентні функції

називаються рівними, якщо їхні типи збігаються. Усюди визначена функція f : A → B називається:

1)однозначною (ін'єкцією) x,y A (fx = fy → x = y) ;

2)сюр'єкцією y B x A y = fx ;

3)взаємооднозначною (бієкцією), якщо вона є ін'єкцією та сюр'єкцією.

1.3.2. ТРАДИЦІЙНІ СПОСОБИ СПЕЦИФІКАЦІЇ ФУНКЦІЙ

У програмуванні означення (дескрипції) функцій називають спе- цифікаціями. Розрізняють теоретико-множинні та процедурні специ- фікації. Перші пов'язані з описом графіків функцій, а другі – безпосе- редньо з описом процедур. Зазвичай з опису графіка функції не ви- пливає її специфікація як процедури. Не завжди за ним, наприклад, можна практично віднайти значення функції на тому чи іншому ар- гументі чи зробити це ефективно. Однак наявність такого опису є важливою передумовою для подальшого уточнення функції, тому ро-

49

ПРОГРАМУВАННЯ

зробник інформаційних систем повинен володіти обома способами специфікації – як теоретико-множинним, так і процедурним.

Оскільки графіки детермінованих функцій є відображеннями, то для їхньої специфікації можна використовувати загальні способи специфікації останніх.

Позначатимемо відображення малими грецькими літерами α,β,γ,K. За означенням образ відображення α(x ) завжди є одноелементним,

тому будемо ототожнювати його із цим елементом, а сам елемент на- зивати значенням відображення α на x і позначати, як і у випадку

про області визначення й значення відображення, а також про ін'єк- тивні, сюр'єктивні та бієктивні відображення. Перші два ще назива-

ють відображеннями в та відображеннями на, відповідно.

Розпочнемо розгляд зі словесного (нематематичного ) способу по- дання відображень. Він може вважатися найбільш універсальним і полягає в тому, що зв'язок між аргументами й результатами відобра- ження формулюється в термінах природної мови. Словесні специфі- кації використовуються насамперед на етапах аналізу вхідних сис- тем, обміну проміжними результатами та інформацією в процесі ро- боти над проектами тощо. Однак за всієї зручності вони мають і сут- тєві недоліки. Існує небезпека неповноти, нечіткості й неоднозначно- сті таких специфікацій. До того ж виникають серйозні проблеми при спробі їхньої процедуризації, тобто при намаганні перейти від слове- сно поданого відображення до еквівалентної йому функції, особливо при автоматизації цих процесів.

Одним із найпростіших і найуживаніших на практиці способів по- дання відображень є табличний. Нехай область визначення відобра-

ження α скінченна й має вигляд Dα = {x1,x2,Kxn }, а Eα = {y1,y2,Kyn },

Лише раз створивши й запам'ятавши таку таблицю, далі можна вже не обчислювати значення відображення, а його результати брати безпо- середньо з таблиці. Таким чином, маємо випадок, коли теоретико- множинне подання прямо входить до специфікації відповідної функції. Воно дуже зручне при проведенні обчислень, зокрема без використання

50