Зубенко, Омельчук - Програмування. Поглиблений курс

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

2.1.4. АБСТРАКТНІ АЛГОРИТМИ

При уточненні поняття алгоритму відійдемо від прийнятої в теорії алгоритмів практики визначати якийсь конкретний клас алгоритмів (машини Тьюрінга чи алгоритми Маркова) і, посилаючись на його універсальність, пов'язувати з ним загальне поняття алгоритму. Такий підхід, прийнятний у світоглядному сенсі, на жаль, майже нічого не дає безпосередньо програмуванню. Тому розглянемо інший підхід, який спирається на загальне поняття функції як обчислювальної про- цедури (див. підрозд. 1.3.4) і реалізацію таких процедур.

Коли говорять про реалізацію класу функцій-процедур чи окремої функції, то мають на увазі, що існує вихідна система Sout = (B,Lâí )

(реальна чи гіпотетична) з Виконавцем, здатним сприймати функції- процедури й проводити за ними конкретні обчислення: фіксувати окремі стани, знаходити значення функції керування на кожному кроці обчислення й виконувати відповідні елементарні перетворення.

Увага! Внутрішня мова програмування системи, що реалізує фун- кції-процедури, не обов'язково вербальна, але обов'язково фінітна – вважається, що Виконавець системи здатен розпізнавати й оперува- ти тільки скінченними за поданням об'єктами ►

Об'єкти внутрішніх мов вихідних систем, що реалізують функціїпроцедури, будемо називати конструктивними, подані в них функції – абстрактними алгоритмами ( А- алгоритмами), а самі внутрішні мови й вихідні системи – алгоритмічними мовами й системами17.

Таким чином, конструктивність об'єкта має сенс тільки в контексті певної алгоритмічної системи (класу систем), а функція-процедура стає А-алгоритмом тільки тоді, коли для неї існує конкретний Виконавець. На вибраному нами пропозиційному рівні абстракції не розглядається вну- трішня структура самих Виконавців (вони теж є чорними скриньками).

Приклад 2.3. Важливий клас А-алгоритмів задають звичайні ари- фметичні вирази й загальні інтерпретовані Ω -терми. Кожен із них визначає певне формальне правило для обчислення значень. Вико- навцем таких алгоритмів може бути, наприклад, особа, яка вміє ана- лізувати структуру термів і виразів і виконувати відповідні операції та предикати. Можна піти ще далі й розглянути всі інтерпретовані регулярні вирази над сигнатурою Ω (див. підрозд. 1.3.3) ■

17 Не випадково перші мови програмування теж називалися алгоритмічними – на-

приклад, Алгол-60 (англ. – ALGOrithmic Language ALGOL-60).

121

ПРОГРАМУВАННЯ

Інші приклади А-алгоритмів – машини Тьюрінга і гра в шахи – детально розглядатимуться нижче.

Відповідності A* та A** , що обчислюються А-алгоритмом A (його

графіки), називаються алгоритмічно обчислювальними. Як і функції, А-алгоритми можуть бути детермінованими й недетермінованими.

Наведемо основні властивості А-алгоритмів, які безпосередньо вип- ливають з їхнього означення.

Масовість. А-алгоритм може бути застосований до будь-якого вхід- ного стану.

Темпоральність. Обчислення за А-алгоритмом відбуваються в глоба- льному часовому просторі, елементи якого можуть впливати на вибір перетворень поточного стану.

Елементарність. У кожний момент часу в обчисленні виконується одна елементарна операція з фіксованої сукупності таких операцій.

Визначеність. Порядок застосування елементарних операцій в обчи- сленні не довільний, а визначається функцією переходу за поточною конфігурацією обчислення.

Результативність. Є механізм завершення обчислень. Фінітність. Скінченність подання А-алгоритму.

Релятивність. Відносність поняття А-алгоритму. Конструктивність А-алгоритму як об'єкта алгоритмічної мови прямо залежить від конкре- тного Виконавця. А-алгоритм даного Виконавця не обов'язково буде А-алгоритмом для іншого. Іншим аспектом релятивності А-алгоритмів є взаємовідносини елементарних операцій і Виконавця. У деяких випад- ках елементарні операції (усі чи їхня частина) можуть вважатися абст- рактними й не підлягати виконанню. Такі операції називаються ораку-

лами, а самі А-алгоритми – А-алгоритмами з оракулами.

Як бачимо, А-алгоритмам притаманні всі основні властивості кла- сичних числових і словарних алгоритмів. Однак з'явилися й нові спе- цифічні риси – темпоральність і релятивність.

У зв'язку з релятивністю виникає задача порівняння різних класів А-алгоритмів за потужністю. Будемо казати, що А-алгоритм A1 з

множиною станів S1 є моделлю А-алгоритму A2 з множиною станів S2 відносно функції кодування ϕ : S2 → S1 , якщо для кожного із вхід- них станів s А-алгоритму A2 виконується A2* (s) = ϕ−1(A1*(ϕs)).

Нехай K1 та K2 – довільні класи А-алгоритмів над обчислюваними просторами Π1 = Γ1,S1 та Π2 = Γ2,S2 , відповідно. Зафіксуємо пев- ну функцію кодування ϕ : S2 → S1 . Кажуть, що клас А-алгоритмів K1

122

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

моделює клас А-алгоритмів K2 , якщо для кожного А-алгоритму з K2 у класі K1 існує його модель. Якщо класи А-алгоритмів моделюють один

одного відносно певних фіксованих функцій кодування, то вони на- зиваються еквівалентними відносно цих функцій.

Фіксуючи конкретні обчислювальні простори Π і відповідних Вико- навців, можна отримати весь спектр класичних алгоритмічних та ігро- вих систем (машини Тьюрінга, алгоритми Маркова й Колмогорова – Ус- пенського, дискретні перетворювачі, трансдюсери, різні класи схем програм, формальні граматики й числення Поста, ігрові числення тощо). Ми це вже бачили на прикладі скінченних і магазинних автоматів (див. підрозд. 1.4.4). Усі перелічені класи класичних алгоритмів і числень є автоматними, еквівалентними й отримали назву універсальних.

Для ілюстрації можливостей А-алгоритмів розглянемо машини Тьюрінга й шахи (відоме ігрове числення) як А-алгоритми.

Виконавець А-алгоритму A , що реалізує машину Тьюрінга, оперує станами, які зображують машинні конфігурації. Такі стани мають два компоненти: перший – внутрішній стан машини, другий подає стан пам'яті машини й має вигляд послідовності комірок, в якій збе- рігається слово в алфавіті X із зазначеною позицією робочої комірки. Часовий простір Γ – натуральний. Значення функції керування на конфігурації визначається внутрішнім станом і станом робочої комі- рки (робочим станом). Воно жодним чином не залежить від номера кроку (часової компоненти) обчислення. Сама дія полягає у зміні Ви- конавцем внутрішнього й робочого станів і позиції робочої комірки. Новою позицією може стати позиція однієї з двох сусідніх комірок у послідовності. Ураховуючи, що сукупності внутрішніх станів Q і ста-

нів робочої комірки X машин Тьюрінга скінченні, функцію переходу нашого А-алгоритму A можна подати теж скінченно, наприклад таб- лично як відповідність δ : Q × X → Q × X × {−1,0,1} , яка за поточними

внутрішнім і робочим станами визначає нові їхні значення й нову по- зицію робочої комірки. Нуль означає, що вона не змінюється, –1 – зсув ліворуч, а 1 – зсув праворуч. Виділяється початковий q0 Q і су-

P на початковому стані є його робочий стан у заключному стані об- числення. Ураховуючи, що є лише один початковий внутрішній стан

123

ПРОГРАМУВАННЯ

А-алгоритму A , можна вважати, що він обчислює словарну відповід- ність A* на множині робочих станів X * .

Нехай X = {|,#} та F = {q* } . Наведена таблиця задає функцію керу- вання А-алгоритму для машини Тьюрінга, яка реалізує додавання на- туральних чисел: початковий стан робочої стрічки |n #|m , де n,m –

довільні натуральні числа, перетворює на |n +m :

Розглянемо таке ігрове числення, як шахи. Особливу увагу зверне- мо на конструктивну (дескрипційну) складову цієї гри. Гра відбува- ється на шаховій дошці – матриці розміром 8 ×8 , клітини якої – поля, мають білий або чорний колір (рис. 2.1).

Рис. 2.1

124

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

Кожна з двох сторін має 16 фігур одного кольору (білого або чорно- го): 8 пішаків, 2 коней, 2 слонів, 2 тури, 1 ферзя й 1 короля. Розташу- вання їх на дошці називається позицією. Можливі такі ходи фігур:

1)пішак може рухатися вперед по вертикалі на одну або дві позиції (останнє можливе тільки тоді, коли він перебуває в початковій позиції). При досягненні восьмої горизонталі (для білих) і першої (для чорних) пі- шак може бути замінений на будь-яку іншу фігуру (але не на короля);

2)тура може рухатися в довільному напрямку по вертикалі або го- ризонталі;

3)слон – те саме, але тільки по діагоналях матриці;

4)кінь ходить буквою Г: спочатку на дві позиції вверх (униз, ліво- руч або праворуч), а потім на одну позицію ліворуч або праворуч, уверх або вниз. Усього можливо до восьми варіантів ходів (на краю дошки кінь має менше ходів);

4)ферзь має можливості тури й слона;

5)король – те саме, що й ферзь, але рух обмежений тільки вісьмома сусідніми клітинами. Окрім цього, у початковій позиції король може зробити рокіровку з однією зі своїх тур за умов: король і тура до цього не рухалися; король не перебуває під шахом (тобто під ударом однієї з фігур супротивника); між турою й королем немає фігур. Рокіровка по- лягає в пересуванні тури впритул до короля й перестрибуванні королем через неї на сусіднє поле. При цьому нові позиції короля й тури не ма- ють бути під ударом супротивника. Рокіровок може бути рівно дві (ко- ротка й довга). Коротка – з турою у стовпчику h, довга – у стовпчику a.

Якщо на шляху фігури (не пішака) стоїть фігура іншого кольору, то вона може бути збита – усунена з дошки. При цьому фігура, що збиває, ставиться на її місце. Пішак збиває не прямо по ходу, а по діагоналі (див. другий хід чорних у "безсмертній" партії нижче). Якщо на шляху фігури стоїть своя фігура, то через неї перестрибувати не можна.

На рис. 2.1 зображено початкову ігрову позицію. Гру починають білі. Кожна зі сторін по черзі робить один із припустимих ходів однією зі сво- їх фігур. Мета гри – створити заключну матову позицію (в якій король не може уникнути збиття) для короля іншої сторони. Заключними є та- кож патові позиції, в яких одна зі сторін позбавлена будь-якого припус- тимого ходу, а також ті позиції, що тричі повторювалися у грі.

Обчисленнями (партіями) у шаховій процедурі є послідовності конфігурацій – позицій фігур на дошці у процесі гри з доданими шіс- тьма прапорцями й одним лічильником. Кожний із прапорців сигна- лізує про наявність чи відсутність першого ходу в партії однієї з шес- ти фігур (по три з кожної сторони), що потенційно можуть брати участь у рокіровці. Прапорець хибний, якщо такого ходу відповідна

125

ПРОГРАМУВАННЯ

фігура ще не зробила. Лічильник показує найбільшу кількість повто- рень однієї з позицій у партії на даний момент часу. Часовий простір

– натуральний. Функція керування шаховою процедурою за поточною позицією і станом прапорців і лічильника повертає сукупність усіх припустимих продовжень гри (припустимих у даний момент ходів) і нові стани прапорців і лічильника. Ураховуючи, що кількість усіх мо-

жливих позицій скінченна (не більше 6416 ×26 ×3 = 3 ×2102 ), обчислен- ня рано чи пізно або перейде в заключний стан, або почне повторю- ватись. Якщо одна з позицій повториться тричі, то гра закінчиться. Щоб зобразити конкретну партію, достатньо задати послідовність хо- дів за білих і чорних. Для цього використовується спеціальна алгори- тмічна мова – шахова нотація. Фігури в ній – кінь, слон, тура, ферзь і король – позначаються відповідно символами К, С, Т, Ф і Кр, пішак не має спеціального позначення. Поля дошки позначаються індексами. По горизонталі вони проіндексовані малими латинськими літерами a, b, c, d, e, f, g, h, а по вертикалі – числами 1, 2, 3, 4, 5, 6, 7, 8. Напри-

клад, пара індексів (а, 1) задає перше поле дошки в рядку а, і це за- писується а1. Один конкретний хід має вигляд:

[<фігура1>][<поле1->][:]< поле2>[<фігура2>] [+|!|!!|?|??|×].

Відсутність першої та присутність другої фігури свідчать про хід пішака. Друга фігура в цьому випадку – це фігура, на яку замінюєть- ся пішак при досягненні по горизонталі краю дошки. Перше поле (необов'язкове) показує, з якого поля йде фігура, а друге – куди. Сим- вол ":" позначає бій фігури, а "+" – напад на короля (шах королю), "×"

– матову позицію, "!" та "!!" – сильний і дуже сильний ходи, "?" та "??" – слабкий і дуже слабкий ходи, відповідно.

Наприклад, початкова позиція (рис. 2.1) зображується так:

Білі: Кр е1, Фd1, Ta1, Th1, Kb1, Kg1, Cc1, Cf1, a2, b2, c2, d2, e2, f2, g2, h2; чорні: Кр е8, Фd8, Ta8, Th8, Kb8, Kg8, Cc8, Cf8, a7, b7, c7, d7, e7, f7, g7, h7.

Така партія називається "дитячий мат": 1. f2–f4 e7–e6 2. g2–g4??

Фh5×.

Тепер розглянемо шахову партію, відому під назвою "безсмертна", що була зіграна в Лондоні в 1851 р. А. Андерсеном і Л. Кизерицьким:

1. е4 е5 /*зліва хід білих, справа – чорних у відповідь, обидва ходи пішаками */2. f4 ef/* хід чорних справа означає e5 : f4 – пішак на e5

б'є сусіднього білого пішака */3. Cc4 Фh4 + 4. Крf1 b5 5. C : b5 Kf6 6. Kf3 Фh6 7. d3 Kh5 8.Kh4 Фg5 9. Kf5 c6 10. g4 Kf6 11. Tg1! Cb 12. h4 Фg6 13. h5 Фg5 14. Фf3 Kg8 15. C : f4 Фf6 16. Kc3 Cc5 17. Kd5 Ф : b2

126

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

18. Cd6 C : g1 19. e5 Ф : a1 + 20. Крe2 Ka6 21. K : g7 + Крd8 22. Фf6 + C : f6 23. Ce7×.

Гра в шахи не є універсальною алгоритмічною системою – кількість її конфігурацій, хоч і астрономічно велика, усе ж скінченна. Однак із погляду конкретних Виконавців вона практично нескінченна, тому завдяки безлічі варіантів ходів та їхніх комбінацій шахи стали чудо- вою моделлю для багатьох реальних задач, пов'язаних із розробкою ефективних стратегій пошуку й обробки інформації в інформаційних системах. Це стосується насамперед перебірних задач у галузях шту- чного інтелекту, прийняття рішень тощо [91].

Як і для загальних функцій, має місце Теорема 2.1 (замкненості). Клас графіків А-алгоритмів замкнений

відносно всіх регулярних композицій. Доведення – див. вправу 34 із підрозд. 1.3 ■

Як і класичні алгоритми, А-алгоритми можуть використовуватись для опису множин. Підмножина станів R S називається розв'язною

(частково розв'язною), якщо існує А-алгоритм A , графік якого збіга- ється з характеристичною функцією χR (частковою характеристич-

ною функцією χR ) підмножини R .

Важливий клас А-алгоритмів складають табличні алгоритми. Нехай часовий простір Γ ізоморфний адитивній групі Z цілих чисел і A – довільна процедура над простором Π = Z,S . Факторизуємо функцію

переходу за часовим аргументом і станами. Зафіксуємо деяку часову константу k ≥ 0 і певне відношення еквівалентності π на станах із S .

Будемо казати, що функція переходу δ періодична за модулем від- ношення π із періодом k (k -періодична за модулем π), якщо для будь-яких еквівалентних станів p та s і довільного моменту часу

t Z виконується δ(t, p) = δ(t + k,s). Функція переходу δ просто пері-

одична за модулем π, якщо вона k -періодична за модулем π для де- якого k . Індексом багатозначної функції назвемо максимальну поту- жність сукупностей значень функції на окремих аргументах. Функція- процедура з періодичною функцією переходу, яка має скінченний ін- декс, а еквівалентність π – скінченний індекс |π| і розв'язні класи,

називається табличним алгоритмом. Табличні алгоритми (T - алгоритми) можна задавати двовимірними таблицями розміром k×|π|: перший вимір відповідає числам від 0 до k −1, другий – кла-

сам еквівалентності π , а в клітинах таблиці розміщуються значення функції переходу. Традиційні алгоритмічні системи зазвичай є табли-

127

ПРОГРАМУВАННЯ

чними як А-алгоритми, а оскільки вони автоматні, то й 1-періодичні за модулем рівності (скінченні автомати, МП-автомати). Машина Тьюрінга є табличним алгоритмом: два її стани еквівалентні, якщо їхні внутрішні стани та стани робочих комірок збігаються.

Для табличних алгоритмів теж має місце теорема замкненості. Теорема 2.2 (замкненості). Клас графіків табличних алгоритмів

замкнений відносно всіх регулярних композицій. Доведення – див. вправу 34 із підрозд. 1.3 ■

А-алгоритми обчислюють і часові оператори, що відображають їхні вхідні конфігурації в заключні, тому вони можуть служити підґрунтям для уточнення й загального поняття обчислювального часового операто- ра в довільній області. Важливо, що цей шлях прямий і не спирається на ті чи інші універсальні числові й словарні моделі таких алгоритмів.

2.1.5. СТРУКТУРНІ АЛГОРИТМИ

Як важливий приклад А-алгоритмів розглянемо клас так званих структурних алгоритмів. Їхній конструктивний опис задають струк- турні блок-схеми (СБС), що є спеціальними графами на площині з трьома типами вершин – прямокутними, ромбічними та еліпсоїдни- ми. Ці графи мають по одній вхідній і вихідній стрілці й побудовані за допомогою композицій із таких базових елементів:

а) оператор

б) умови:

в) стрілки: г) символи: +,- .

Найпростіша СБС будується з оператора і двох стрілок: x

Нехай

– довільні блок-схеми. Розглянемо композиції, за допомогою яких із наведених блок-схем і базових елементів будуються нові СБС.

128

Розділ ІІ. ЕЛЕМЕНТИ ІНФОРМАТИКИ

Послідовне з'єднання. Його результатом є складена СБС:

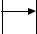СБС1 СБС2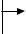

Розгалуження:

СБС1 СБС2

Обхід:

СБС

Вибір:

…

СБС1 СБС2 … СБСn

Детермінований вибір. Цю композицію можна отримати з ком- позиції вибору, якщо деякі або всі вершини-ромби замінити на вер- шини-еліпси. Наприклад:

129

ПРОГРАМУВАННЯ

СБС1 СБС2 СБC3

При інтерпретації вершини-еліпси будуть відповідати заключним охоронам.

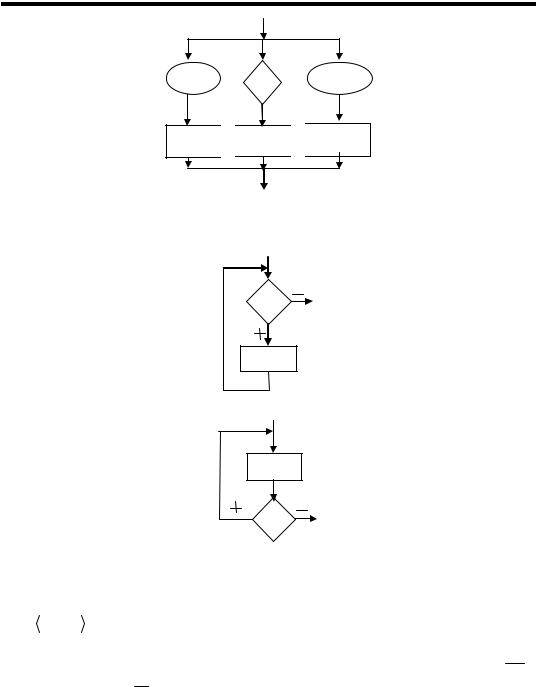
Ітерація:

СБС

Повторення:

СБС

Структурні блоксхеми – це елементи замкнення базових елементів відносно наведених вище структурних композицій.

Як елементи замкнень усі СБС є скінченними об'єктами. Нехай Π = Γ,S, – обчислювальний простір із натуральним часом Γ = N ,

множиною станів S та = {ϕ1,...,ϕk } {γ1,...,γl } – сукупністю елемен- тарних перетворень станів і предикатів на них, ϕi : S → S , i =1,k , γj : S → Bool , j =1,l . Інтерпретацією блок-схеми A називається пара

130