
С доказательством
.pdf1. Біном Ньютона ;
n
a, b R n N справджується рівність: (a b) n Cnk a k b n k
k 0
Доведення. Спочатку безпосередньо з означення доведемо просту, але дуже важливу властивість біноміальних коефіцієнтів:
k |
k 1 |
|
n! |
|
n! |
|
n! |
|
1 |
|
1 |
|
|||
Cn |
Cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k!(n k )! |
(k 1)!(n k 1)! |
|
|
|
|||||||||||
|
|
|
|
|
(k 1)!(n k )! k |
|
n k 1 |
|
|||||||
|
|
n! |
|
n k 1 k |
|
n!(n 1) |
C k |
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
(k 1)!(n k)! |
|
k(n k 1 |
k!(n k 1)! |
n 1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
Тепер можемо скористатися математичною індукцією. При n 1 |
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
(a b) C1k a k b1 k a b - справджується. |
|
|
|
|
|
|||||||||
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
Нехай при деякому n N виконується (a b) n Cnk a k b n k , треба довести, що |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
(a b) n 1 Cnk 1a k b n 1 k . |
|
|
|
|
|
|
|
|
||||||
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
n |
|
|
|
n |
n |
|
|
(a b) n 1 (a b) n (a b) (a b) Cnk a k b n k Cnk a k 1b n k Cnk a k b n k 1 |
|
|||||||||||||
|
|
|
|
|
|
|
k 0 |
|
|
k 0 |
k 0 |
|
|
|
|
|
n 1 |
|
n |
|
|
|
|
|
n |
|
|
||
a n 1 Cnk a k 1b n k Cnk a k b n 1 k |
b n 1 a n 1 |
Cnk 1a k b n 1 k |
|
|
||||||||||
|
|
k 0 |
|
k 1 |
|
|
|
|
|
k 1 |
|
|
||
n |
|
|
|
|
|
n |
Cnk a k b n 1 k |
|
|
|
||||
Cnk a k b n 1 k |
b n 1 a n 1 Cnk 1 |
b n 1 a n 1 |
|
|
||||||||||
k 1 |
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
n |
1a k bn 1 k b n 1 (a b)n 1 , що й треба було довести. |
|
|
|||||||||||
Cnk |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k 1
Теорема доведена.

2. Нерівність Бернуллі;
Нерівність Бернуллі стверджує: якщо  , то
, то
 для всіх
для всіх
Однак, узагальнена нерівність Бернуллі стверджую наступне:
якщо  , то
, то 
якщо  , то
, то 
при цьому рівність досягається в двох випадках:
Доведення. Доведення  проводиться методом математичної індукції по n. При n = 0 нерівність, очевидно, вірна. Припустимо, що вона вірна для n, доведемо це вірно для n+1:
проводиться методом математичної індукції по n. При n = 0 нерівність, очевидно, вірна. Припустимо, що вона вірна для n, доведемо це вірно для n+1:
3. Зв’язок між найбільшим елементом та супремумом;
(Зв’язок між найбільшим елементом та супремумом).
Нехай xmax найбільший елемент множини X , тоді ця множина обмежена і sup X xmax .
Доведення. Оскільки xmax - найбільший елемент, то x X x xmax X обмежена зверху множина та xmax її мажоранта. Якщо x довільна мажоранта x X x x , але з того, що xmax X xmax x , тобто xmax найменша мажоранта xmax sup X .
Теорема доведена.
4. Зв'язок між найменшим елементом та інфінумом;
(Зв’язок між найменшим елементом та інфінумом).
Нехай xmin найменший елемент множини X , тоді ця множина обмежена і inf X xmin .
Доведення. Оскільки xmin - найменший елемент, то x X x xmin X обмежена знизу множина та xmin її міноранта. Якщо x довільна міноранта x X x x , але з того, що xmin X xmin x , тобто xmin найбільша міноранта xmin inf X .
Теорема доведена.

5. Теорема про перехід до верхньої межі в нерівностях;
(Перехід до верхньої межі в нерівностях).
Нехай x X x b . Якщо X має верхню межу, то sup X b .
Доведення. b - є мажорантою X , а sup X - найменша з мажорант, з чого безпосередньо слідує, що sup X b .
Теорема доведена.
6. Теорема про перехід до нижньої межі в нерівностях;
(Перехід до нижньої межі в нерівностях).
Нехай x X x b . Якщо X має нижню межу, то inf X b .
Доведення. b - є мінорантою X , а inf X - найбільша з мінорант, з чого безпосередньо слідує, що inf X b .
Теорема доведена.
7. Єдиність границі збіжної числової послідовності;
Послідовність не може мати більше однієї границі.
Доведення. Припустимо, що послідовність { xn } має дві границі a і b, не рівні один одному.
xn ® a; xn ® b; a ¹ b.
Тоді за визначенням існує таке число e >0, що
Запишемо вираз:
Атому що e – будь-яке число, те  , тобто a = b. Теорему доведено
, тобто a = b. Теорему доведено
8.Теорема про три послідовності;
Нехай задані 3 послідовності  задовольняють умови:
задовольняють умови:

1)існує  - число,
- число,
2)існує  , що для будь-якого
, що для будь-якого  .
.
Тоді існує |
. |
|
|
|
Доведення. Нехай зафіксовано |
. Тоді, за означенням, існують такі n0',n0'', що для |
|||
всіх |
|
, а для всіх |
|
. |
Позначимо через n0 |
найбільший з номерів n0',n0''. Тоді для |
|
|
|
всіх |
|
, тоді оскільки |
, |
|
то |
, а це означає, що |
. |
|
|
9.
1.O(1) O(1) O(1) (сума двох обмежених – обмежена);
2.o(1) o(1) o(1) (сума двох нескінченно малих – нескінченно мала);
3.O(1) o(1) O(1) ;
4.O(1) O(1) O(1) (добуток двох обмежених – обмежена);
5. |
o(1) o(1) |
o(1) (добуток |
двох нескінченно малих |
– нескінченно |
|
|
|||||
|
мала); |
|
|
|
|
6. |
O(1) o(1) |
o(1) |
(добуток |
нескінченно малої на |
обмежену є |
|
|
|
|||
нескінченно малою).
7.O(1) O(1) O(1) ;
8.o(1) o(1) o(1) ;
9.C O(1) O(1) C const ;
10.C o(1) o(1) C const .
10.Сумою, xn та yn з R називаються відповідно послідовність - xn yn .
Границя суми дорівнює сумі границь.
Доведення. Нехай, |
наприклад, |
, |
. |
Покажемо, |
що  . Дійсно
. Дійсно

 ;
;
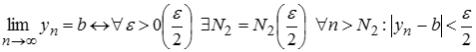 .
.
За  оберемо
оберемо 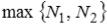 та оцінимо модуль
та оцінимо модуль  , маємо:
, маємо:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
Таким чином, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11. |
|
|
Добутком xn та yn з R називаються відповідно послідовності - |
xn yn . |
|
|
|
|||||||||||||||||||||||||||||||||||||||
12. |
|
|
Часткою послідовностей xn та |
yn з R називаються відповідно послідовності - |
||||||||||||||||||||||||||||||||||||||||||
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
, вважаємо |
yn 0 . Останнім обмеженням можна знехтувати, |
якщо розглядати |
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
послідовності xn та yn з простору |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
x |
|
. |
||||||||||||||||||||||||||
R |
, тоді можна вважати |
x R \ |
|
|||||||||||||||||||||||||||||||||||||||||||
0 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
lim |
xn |
|
x |
y 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
n y |
n |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Доведення. З теореми 6 запишемо послідовності |
xn x o(1) yn y o(1) , тоді |
|||||||||||||||||||||||||||||||||||||||||
одержимо. xn yn x o(1) y o(1) |
x y o(1) твердження 1. доведено. |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
З теореми 4 |
послідовності |
xn , yn обмежені, |
тобто дорівнюють O(1) , |
а тому |
||||||||||||||||||||||||||||||||||||||
|
xn yn (x o(1))(y o(1)) xy xo(1) yo(1) o(1)o(1) xy o(1) , |
твердження |
2. |
|||||||||||||||||||||||||||||||||||||||||||
доведено. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Оскільки yyn |
y |
2 |
y 2 |
, |
то |
N : |
n N |
yyn |
y 2 |
|
, а |
|
тому |
|
1 |
|
|
|
|
|
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
yy n |
|
y 2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
O(1) (лема |
|
1), |
|
тому |
1 |
|
1 |
|
|
y yn |
( y yn ) |
1 |
|
o(1)O(1) o(1) |
і |
||||||||||||||||||||||||||||
|
yy n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
yn |
|
|
y |
yyn |
|
yyn |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
твердження 3. доведеною. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Тепер з останніх двох властивостей одержимо: |
xn |
xn |
1 |
|
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
yn |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема доведена.
13. Теорема Вейєрштрасса про iснування границi монотонної обмеженої послiдовностi.
Якщо послідовність монотонна і обмежена, то вона збіжна.
Доведення (для випадку монотонно не спадної послідовності (an)). Розглянемо
множину  , яка складається з елементів цієї послідовності. Тоді А - обмежена зверху, бо послідовність (an) обмежена за мовою теореми. Звідси, за теоремою про існування супремуму, існує
, яка складається з елементів цієї послідовності. Тоді А - обмежена зверху, бо послідовність (an) обмежена за мовою теореми. Звідси, за теоремою про існування супремуму, існує  Доведемо, що
Доведемо, що  .
.
Нехай  заданий. Існує
заданий. Існує  , такий, що
, такий, що  ,
,
бо інакше для всіх  . Тоді
. Тоді 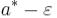 - верхня межа А, менша
- верхня межа А, менша
за  , а це неможливо. Оскільки (an) - не спадна, то із (1) випливає, що для
, а це неможливо. Оскільки (an) - не спадна, то із (1) випливає, що для
всіх  . Звідси, для всіх
. Звідси, для всіх  .
.
Номер n0 - шуканий. Теорему доведено.
14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число e. Довести збiжнiсть послiдовностi xn = (1+1/n) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
2 |
|
|
1 |
|
3 |
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
xn |
1 |
|
|
|
|
|
|
1 |
|
|
Cn |
|
|
|
|
|
|
Cn |
|
|
|
|
|
Cn ... |
|
|
|
|
|
Cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
n |
|
n |
n2 |
n3 |
|
nn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
1 |
|
n |
1 |
|
|
|
|
|
n(n 1) |
|
|
1 |
|
|
n(n 1)(n 2) |
|
... |
1 |
|
n(n 1)(n 2)...1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n 2 |
|
|
|
|
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n n |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 1 |
1 |
1 |
1 |
|
|
1 |
1 |
1 |
2 |
|
1 |
|
|
... |
1 |
1 |
|
1 |
2 |
... 1 |
n 1 |
|
|
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
n 2! |
|
|
|
|
|
|
|
|
n |
|
|
n |
3! |
|
|
|
n |
|
|
|
n |
|
|
|
n n! |
|
||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
... 1 |
|
|
1 |
|
1 |
|
2 |
|
... 1 |
n 1 |
|
1 |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
1 2! |
|
|
|
|
n 1 |
|
1 3! |
|
|
|
|
|
|
|
n 1 |
1 |
|
|
|
n 1 n! |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
1 |
|
|
2 |
|
|
... 1 |
n 1 |
|
1 |
n |
|
|
|
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
n 1 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
n 1 (n 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
як легко побачити, порівнюючи відповідні |
доданки |
|
у |
|
|
xn |
і xn 1 , ця послідовність |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
зростаюча. |
|
Крім |
|
того |
|
|
|
|
|
з |
нерівності |
|
легко |
|
|
|
|
одержати |
|
таке |
обмеження: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xn 2 |
|
|
1 |
|
|
1 |
|
|
... |
1 |
|
|
|
zn 2 |
|
1 |
|
|
|
1 |
|
... |
|
|
|
1 |
|
|
3 |
, а тому |
xn |
|
як і zn є |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2n 1 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2! 3! |
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
монотонними та обмеженими (монотонність zn очевидна). Тому вони обидві збіжні.
Границю послідовності xn називають числом e 2,718281... .
15. Довести оцiнку 1/(n+1) < ln(1 + 1/n) < 1/n.
Доведення:
|
|
|
1 |
n 1 |
|
|
1 |
|
|
yn |
1 |
|
|
|
xn 1 |
|
|
|
e 1 e |
|
|
||||||||
|
|
|
n |
|
|
n |
|
||
|
|
|
1 |
n |
xn e yn |
1 |
|
|
|
|
||||
|
|
|
n |
|
|
|
1 |
n 1 |
e 1 |
|
|
|
|
|||
|
|
n |
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|||
n ln 1 |
|
|
|
1 (n 1) ln 1 |
|
|
. |
n |
|
|
|
n 1 . |
|
|
ln 1 |
|
|
|
|
|
. |
|
|
ln 1 |
1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
n |
|
|
n |
|
|
n 1 |
|
|
n |
|
n |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
Що й треба було довести. |
|
|
|
|
|
|
|
|
16. Довести, що 2+1/2! +1/3! + ... + 1/n! → e при n →∞. |
|
|
|
|
при n , ми |
|||
(Продовження 14) Зробимо в цій нерівності граничний перехід |
||||||||
одержимо, що ліва частина прямує до e , а права до виразу 2 |
1 |
|
|
1 |
|
... |
1 |
zk . З |
|
|
|
|
|
||||
|
2! |
3! |
k ! |
|||||
теореми про перехід до границі в нерівностях одержимо, що |
k N xk zk e , а |
|||||||
тому з теореми про двох поліцаїв lim zk e . |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
17. Стала Ейлера C. Довести формулу 1+1/2 +1/3 + ... + 1/n = C + ln n + o(1).
18. Теорема про збiжнiсть довiльної пiдпослiдовностi збiжної послiдовностi.
(Підпослідовності збіжної послідовності). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Нехай послідовність xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
збігається |
і |
lim xn |
a R . |
Тоді |
будь-яка |
її |
|||||||||||||
підпослідовність xn |
також збіжна і lim xn |
n |
|
|
|
|
|
|
|
|
|
|
|
||||||
a . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
k |
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доведення. Нехай yk xn |
|
довільна |
|
|
підпослідовність послідовності |
xn . За |
|||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
означенням границі: 0 |
N : n N |
|
xn a |
|
. З того, |
що nk - |
зростаюча |
||||||||||||
|
|
||||||||||||||||||
послідовність натуральних |
чисел, |
зрозуміло, що |
nk |
K N : |
k K |
||||||||||||||
nk N . Поєднуючи два останні твердження, |
ми одержимо, |
що 0 K : k K |
|||||||||||||||||
|
|
|
|
|
, з чого слідує, що yk a при k . |
||||||||||||||
nk N |
xn |
a |
|
yk |
a |
||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема доведена.
19. Критерiй Кошi збiжностi числової послiдовностi.
(Критерій Коші)
Послідовність xn дійсних чисел збігається тоді і тільки тоді, коли вона фундаментальна
|
Доведення. Необхідність. Нехай існує lim xn x . Тоді 0 N : n N : |
|||||||||||||||||
|
|
|
|
|
|
|
n |
|
||||||||||
|
xn x |
|
n N p N |
|
xn p xn |
|
|
|
xn p x |
|
|
|
xn x |
|
2 . |
|||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
Необхідність доведена. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Достатність. Якщо |
xn - фундаментальна, то вона обмежена, (див лему 1 з розділу |
||||||||||||||||
1.4). За теоремою Больцано-Вейєрштрасса існує збіжна підпослідовність xn |
. Із означення |
|||||||||||||||||
|
|
|
|
0 1 xk |
|
|
|
|
|
|
|
|
|
|
|
k |
||
фундаментальності xk xn |
xn |
0 1 , а далі за теоремою про суму двох |
||||||||||||||||
|
|
|
|
k |
|
|
k |
|
||||||||||
збіжних послідовностей, одержимо, що xk |
збігається. |
|
||||||||||||||||
|
Достатність доведена. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Теорема доведена. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
20. Критерій збіжності послідовності через верхню та нижню границі |
|
|
|
||||||
Для будь-якої обмеженої послідовності xn виконується нерівність |
|
|
|
||||||
lim xn limxn |
|||||||||
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
lim xn . |
|
|
|
. Рівність можлива тоді і тільки тоді, коли lim xn |
limxn |
|
|
|
|||||
|
n |
n |
n |
|
|
|
|||
Доведення. З очевидної нерівності n N inf xk sup xk слідує бажана нерівність, |
|||||||||
|
|
k n |
|
|
k n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
якщо зробити відповідний граничний перехід при n . |
|
|
|
|
|||||
|
|||||||||
Необхідність. Нехай тепер lim xn |
lim |
xn . Оскільки n N inf xk xn sup xk . |
|||||||
n |
n |
|
|
|
k n |
|
k n |
||
|
|
|
|
|
|
|
|
||
Далі, границя лівої та правої частини співпадають, з чого слідує існування границі середньої послідовності.
|
Достатність. |
Нехай тепер існує lim xn a . |
Тоді 0 |
N : n N |
|
|||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
xn a |
|
, |
|
|
тобто |
a xn a |
|
a inf xk a |
|
||
|
|
|
|
|||||||||
a sup xk a , |
|
|
k n |
|
||||||||
але це означає, |
що |
liminf xk |
lim xn a |
|||||||||
|
|
|
k n |
|
|
|
|
|
|
n k n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
lim sup xk lim xn |
a . |
|
|
|
|
|
|||||
n k n |
n |
|
|
|
|
|
|
|||||
Теорема доведена.
