
Ряды_Доказательства
.docx1)Відсутність рівномірної збіжності добутку для загального випадку
Розглянемо
приклад:
 ,
,
 ,
,
 ,
,
 .
За побудовою очевидно, що
.
За побудовою очевидно, що
 ,
,
 .
Функція
.
Функція
 ,
,
 .
Тепер знайдемо
.
Тепер знайдемо
 при
при
 ,
що й треба було показати.
,
що й треба було показати.
2) Властивості СР – диференційованість

3) Властивості СР – інтегрованість

4) Властивості СР – неперервність
Cлiдує
з рівномірної збіжності
СР в крузі

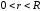
5) Єдиність рівномірної границі ФП
|
|
Якщо на
множині
|
Доведення: Якщо на множині

 ,
то на
,
то на
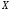 також
також
 ,
,
а поточкова границя f – єдина.
|
|
6)
Збіжність ряду
Степеневий ряд
|
Доведення.
Якщо
 ,
то розбіжність цього ряду слідує з
необхідної умови збіжності ряду, тобто
загальний член ряду не прямує до нуля.
Нехай тепер
,
то розбіжність цього ряду слідує з
необхідної умови збіжності ряду, тобто
загальний член ряду не прямує до нуля.
Нехай тепер
 ,
використаємо теорему, розглянемо ряд
,
використаємо теорему, розглянемо ряд
 ,
а це є геометрична прогресія із знаменником
,
а це є геометрична прогресія із знаменником
 .
Цей ряд збіжний при
.
Цей ряд збіжний при
 ,
тобто при
,
тобто при
 ,
та розбіжний в іншому випадку.
,
та розбіжний в іншому випадку.
7) Збіжність степенево-логарифмічного ряду
Ряд
 збіжний при
збіжний при
 ,
та розбіжний при
,
та розбіжний при
 .
.
Знову розглянемо рівнозбіжний
ряд, про який йдеться у відповідній
теоремі.
 ,
а далі залишається скористатися
збiжнiстю
,
а далі залишається скористатися
збiжнiстю
8) Зв'язок абсолютної та простої збіжності ЧР
Якщо ряд
 абсолютно збіжний, то він є збіжним
абсолютно збіжний, то він є збіжним
Доведення. Запишемо критерій
Коші збіжності ряду
 :
:

 :
:



 .
Але звідси слідує нерівність
.
Але звідси слідує нерівність
 ,
а тому для ряду
,
а тому для ряду
 виконується критерій Коші, а тому цей
ряд збіжний.
виконується критерій Коші, а тому цей
ряд збіжний.
9)
Зв'язок збіжності ЧР та його
 -залишку
-залишку
Ряд
 збігається чи розбігається одночасно
з своїм
збігається чи розбігається одночасно
з своїм
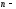 залишком.
Якщо ряд збігається, то його
залишком.
Якщо ряд збігається, то його
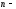 залишок
збігається до нуля.
залишок
збігається до нуля.
Доведення. Якщо ряд
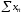 збіжний і його сума
збіжний і його сума
 ,
тоді
,
тоді
 ,
де послідовність
,
де послідовність
 як раз і є
як раз і є
 залишком
цього ряду. З відомої теореми з теорії
послідовностей слідує, що
залишком
цього ряду. З відомої теореми з теорії
послідовностей слідує, що
 .
Аналогічно розглядається випадок
розбіжного ряду.
.
Аналогічно розглядається випадок
розбіжного ряду.
Наслідок доведено.
10) Зв'язок поточкової та рівномірної збіжності ФП
Якщо на множині

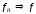 ,
то на
,
то на
 також
також
 .
.
Доведення. З означення
рівномірної збіжності можемо записати
оцінку:

 ,
з якої все слідує.
,
з якої все слідує.
11) Інтегрування неперервної ФП
Якщо ФП
 на
на
 і
і

 ,
то
,
то
 і цю ФП можна інтегрувати почленно,
тобто
і цю ФП можна інтегрувати почленно,
тобто
 .
.
Доведення. Умова
 безпосередньо слідує з умови
безпосередньо слідує з умови
 .
.
З умови
 слідує, що
слідує, що

 :
:


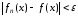 .
З теореми 1
.
З теореми 1


 ,
а далі легко одержимо:
,
а далі легко одержимо:

12) Критерій збіжності знакосталого ряду
Ряд
 збiжний
постiдовнiсть
його часткових сум
збiжний
постiдовнiсть
його часткових сум
 - обмежена.
- обмежена.
Доведення:
Якщо хn – додатня
, то
 монотонно зростаюча.
монотонно зростаюча.
 збiжний
існує і є скінченною границя послідовності
часткових сум ряду
збiжний
існує і є скінченною границя послідовності
часткових сум ряду
 - обмежена.
- обмежена.
13) Критерій Коші для ЧР
Ряд
 збігається тоді і тільки тоді, коли
збігається тоді і тільки тоді, коли
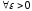
 :
:


 .
.
Доведення: Запишемо критерій Кошi для Sn.

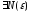 :
:

 |Sn+p
– Sn|
= |xn+1
+ … + xn+p
| =
|Sn+p
– Sn|
= |xn+1
+ … + xn+p
| =

14)Критерій Коші рівномірної збіжності ФП
ФП
 рівномірно збіжна тоді і тільки тоді,
коли вона рівномірно фундаментальна
рівномірно збіжна тоді і тільки тоді,
коли вона рівномірно фундаментальна
Доведення. Необхідність.



 :
:


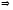



 необхідність доведена.
необхідність доведена.
Достатність.
 маємо оцінку
маємо оцінку
 ,
яка виконується для всіх натуральних
,
яка виконується для всіх натуральних
 .
З цього слідує фундаментальність
числової послідовності
.
З цього слідує фундаментальність
числової послідовності
 при довільному фіксованому
при довільному фіксованому
 .
А тому існує
.
А тому існує
 ,
яку ми позначимо
,
яку ми позначимо
 .
Виберемо довільне
.
Виберемо довільне
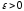 ,
оскільки
,
оскільки
 - рівномірно фундаментальна, то
- рівномірно фундаментальна, то
 :
:





 в останній нерівності перейдемо до
границі при
в останній нерівності перейдемо до
границі при
 .
Дістанемо, що
.
Дістанемо, що

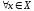 виконується нерівність
виконується нерівність
 .
Перейдемо до супремуму по
.
Перейдемо до супремуму по
 одержимо, що
одержимо, що
 ,
звідки і слідує, що
,
звідки і слідує, що
 .
.
Теорема доведена
15) Лінійність збіжності рядів
Нехай
ряди
 та
та
 збігаються,
збігаються,
 ,
тоді ряд
,
тоді ряд
 також збігається, та для його суми
виконується рівність:
також збігається, та для його суми
виконується рівність:
 .
.
16) Лінійність рівномірної збіжності
Якщо
на множині

 ,
,
 ,
то
,
то
 виконується умова:
виконується умова:
 .
.
Доведення:
||α fn
+ β gn
- α f - β
g|| ≤ |α| ||
fn
– f || + |β|
|| gn
– g ||

17) Мажорантна ознака збіжності знакосталого ряду
Нехай
послідовність
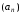 є мажорантою для послідовності
є мажорантою для послідовності
 ,
то: якщо ряд
,
то: якщо ряд
 збіжний, то ряд
збіжний, то ряд
 також збіжний; навпаки, з умови розбіжності
ряду
також збіжний; навпаки, з умови розбіжності
ряду
 слідує також розбіжність ряду
слідує також розбіжність ряду

Доведення: Нехай ряд
 збіжний, тоді послідовність його
часткових сум
збіжний, тоді послідовність його
часткових сум
 монотонно зростає і обмежена. З умови
монотонно зростає і обмежена. З умови
 слідує, що
слідує, що
 ,
де
,
де
 .
Але тоді послідовність
.
Але тоді послідовність
 також є обмеженою, крім того вона
монотонно зростає, а тому є збіжною. З
цього і слідує збіжність ряду
також є обмеженою, крім того вона
монотонно зростає, а тому є збіжною. З
цього і слідує збіжність ряду
 .
.
Якщо ряд
 розбіжний, то послідовність
розбіжний, то послідовність
 необмежена, але тоді і послідовність
необмежена, але тоді і послідовність
 також не обмежена, бо вона мажорує
послідовність
також не обмежена, бо вона мажорує
послідовність
 .
З цього слідує розбіжність ряду
.
З цього слідує розбіжність ряду
 .
.
18) Не еквівалентність абсолютної та простої збіжності рядів
Для цього достатньо розглянути
такий ряд:
 .
.
Як слідує з збіжності
степеневого ряду ряд, що складається з
модулів
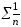 є розбіжним.
є розбіжним.
З
теорії послідовностей ми знаходили
границю такої послідовності:
 а це означає збіжність вказаного ряду.
а це означає збіжність вказаного ряду.
19) Необхідна умова збіжності ряду
Якщо
ряд
 збігається, то послідовність його
загальних членів прямує до нуля.
збігається, то послідовність його
загальних членів прямує до нуля.
Доведення.
Якщо
 - збіжний, то послідовність його часткових
сум має границю, позначимо її як
- збіжний, то послідовність його часткових
сум має границю, позначимо її як
 .
Але тоді
.
Але тоді
 .
.
20) Необхідна умова розвинення функції в СР
Для
того, щоб функцію
 можна було розкласти в СР на проміжку
можна було розкласти в СР на проміжку
 ,
необхідно, щоб вона мала на цьому проміжку
неперервні похідні довільного порядку.
,
необхідно, щоб вона мала на цьому проміжку
неперервні похідні довільного порядку.
Доведення: наслiдок з властивостей СР.
21) Ознака Абеля
Якщо
ряд
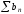 збігається, а послідовність
збігається, а послідовність
 (з
обмеженою варіацією), то ряд
(з
обмеженою варіацією), то ряд
 - збіжний.
- збіжний.
Доведення.
Із збіжності ряду
 слідує, що послідовність його часткових
сум
слідує, що послідовність його часткових
сум
 - збіжна, а тому і обмежена, крім того
послідовність
- збіжна, а тому і обмежена, крім того
послідовність
 збіжна, як добуток двох збіжних
послідовностей, а далі усе слідує з
ознаки Абеля-Діріхле
збіжна, як добуток двох збіжних
послідовностей, а далі усе слідує з
ознаки Абеля-Діріхле
22) Ознака Абеля-Діріхле
Нехай
для послідовностей
 виконуються такі умови:
виконуються такі умови:
 ,
,
 ,
послідовність
,
послідовність
 збіжна в
збіжна в
 ,
то ряд
,
то ряд
 - збіжний.
- збіжний.
Доведення.
Оскільки ряд
 абсолютно збіжний, а
абсолютно збіжний, а
 ,
то ряд
,
то ряд
 також абсолютно збіжний (а тому і просто
збіжний), що слідує з мажорантної ознаки
для рядів. Із збіжності послідовності
також абсолютно збіжний (а тому і просто
збіжний), що слідує з мажорантної ознаки
для рядів. Із збіжності послідовності
 та з теореми про рівнозбіжність рядів,
що пов’язані перетворенням Абеля
та з теореми про рівнозбіжність рядів,
що пов’язані перетворенням Абеля
слідує також збіжність ряду
 ,
що й треба було довести.
,
що й треба було довести.
23) Ознака Вейєрштрассса рівномірної збіжності ФР
Нехай
для ФР
 існує така числова послідовність
існує така числова послідовність
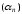 ,
що ряд
,
що ряд
 - абсолютно збіжний та
- абсолютно збіжний та
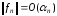 ,
тоді ряд
,
тоді ряд
 збігається рівномірно.
збігається рівномірно.
Доведення. З відповідної
теореми про мажорантну ознаку збіжності
слідує, що ряд
 - збіжний, а тому ряд
- збіжний, а тому ряд
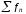 - рівномірно збіжний.
- рівномірно збіжний.
24) Ознака Гаусса
Якщо для ряду
 виконується умова
виконується умова
 ,
де
,
де
 ,
,
 ,
,
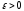 - сталі, а послідовність
- сталі, а послідовність
 ,
то ряд
,
то ряд
 :
:
-збіжний, якщо
 ,
або
,
або
 ;
;
-
розбіжний , якщо
 ,
або
,
або
 .
.
Доведення.
Випадок
 безпосередньо слідує з ознаки д’Аламбера.
Випадок
безпосередньо слідує з ознаки д’Аламбера.
Випадок
 - це наслідок з ознаки Раабе. Залишається
розглянути випадок
- це наслідок з ознаки Раабе. Залишається
розглянути випадок
 .
Тобто ми маємо рівність:
.
Тобто ми маємо рівність:
 .
Застосуємо ознаку Куммера, вибравши в
якості послідовності
.
Застосуємо ознаку Куммера, вибравши в
якості послідовності
 ,
степенево-логарифмічний ряд
,
степенево-логарифмічний ряд
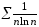 розбіжний. Тоді маємо:
розбіжний. Тоді маємо:

 .
.
Перший
доданок прямує до нуля, а другий до
 ,
тому що для логарифму можна скористатися
відомою формулою еквівалентності:
,
тому що для логарифму можна скористатися
відомою формулою еквівалентності:
 .
Таким чином
.
Таким чином
 ,
і з ознаки Куммера цей ряд розбіжний.
,
і з ознаки Куммера цей ряд розбіжний.
25) Ознака д’Аламбера
Якщо для ряду
 існує границя
існує границя
 ,
тоді: якщо
,
тоді: якщо
 ,
то ряд
,
то ряд
 - збіжний; якщо
- збіжний; якщо
 ,
то ряд
,
то ряд
 - розбіжний
- розбіжний
Доведення.
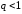 випливає з узагальненої
ознаки д’Аламбера
випливає з узагальненої
ознаки д’Аламбера
 Виберемо число
Виберемо число
 таким, щоб виконувались умови:
таким, щоб виконувались умови:
 .
Тоді, починаючи з деякого номера
.
Тоді, починаючи з деякого номера
 ,
одержимо, що
,
одержимо, що




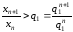 ,
і за порiвняльною
ознакою ряд
,
і за порiвняльною
ознакою ряд
 розбіжний.
розбіжний.
26) Ознака Діріхле
Якщо послідовність
 ,
і
,
і
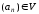 ,
а для послідовності
,
а для послідовності

 ,
то ряд
,
то ряд
 - збіжний
- збіжний
Доведення. З умов
 та
та
 слідує, що послідовність
слідує, що послідовність
 ,
тобто збіжна, а далі все слідує з теореми
Абеля-Діріхле.
,
тобто збіжна, а далі все слідує з теореми
Абеля-Діріхле.
27) Ознака Лейбниця
Якщо послідовність
 ,
і
,
і
 ,
то ряд
,
то ряд
 - збіжний
- збіжний
Доведення. Покладемо
 ,
тоді очевидно, що послідовність
,
тоді очевидно, що послідовність
 ,
і далі за ознакою Дiрiхле.
,
і далі за ознакою Дiрiхле.
28) Ознака Раабе
Якщо для ряду
 виконується умова
виконується умова
 ,
то при
,
то при
 цей ряд збігається, а при
цей ряд збігається, а при
 - розбігається.
- розбігається.
Доведення.
Застосуємо ознаку Куммера, поклавши
 ,
зрозуміло, що при цьому ряд
,
зрозуміло, що при цьому ряд
 - розбіжний. Тоді
- розбіжний. Тоді
 ,
а далі залишається використати ознаку
Куммера в граничній формі.
,
а далі залишається використати ознаку
Куммера в граничній формі.
29) Перетворення Абеля
Для будь-якого натурального
 та послідовностей
та послідовностей
 виконується рівність (перетворення
Абеля):
виконується рівність (перетворення
Абеля):

Доведення.


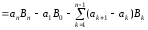
30) Перехід до границі ФП
Нехай ФП
 на
на
 і
і

 (
( - гранична точка множини
- гранична точка множини
 ),
то
),
то
 та виконуються рівності:
та виконуються рівності:
 .
.
Доведення: Це є переформулювання теореми на випадок ФП
31) Порівняльна ознака збіжності знакосталого ряду
Якщо ряд
 збіжний, та існує номер
збіжний, та існує номер
 ,
починаючи з якого
,
починаючи з якого
 виконуються нерівності
виконуються нерівності
 ,
то ряд
,
то ряд
 також збіжний.
також збіжний.
Доведення.
Перепишемо задану нерівність у вигляді:

 ,
а тому виконується така оцінка
,
а тому виконується така оцінка

 .
А тому
.
А тому
 ,
тобто
,
тобто
 ,
і за мажорантною ознакою ряд
,
і за мажорантною ознакою ряд
 збіжний.
збіжний.
32) Приклад до зв’язку між ознаками д’Аламбера
|
Покажемо,
що з умови
|
|
Розглянемо
ряд
Якщо
ж розглянути відношення
|
33) Про додатну та від’ємну частини збіжного ряду (умовно чи абсолютно)
Якщо ряд
 збігається абсолютно, то також збігаються
одночасно і ряди
збігається абсолютно, то також збігаються
одночасно і ряди
 ,
,
 .
Якщо ж ряд
.
Якщо ж ряд
 збігається умовно, то обидва ряди
збігається умовно, то обидва ряди
 ,
,
 одночасно розбігаються.
одночасно розбігаються.
Доведення. Нехай ряд
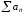 збігається абсолютно, позначимо
збігається абсолютно, позначимо
 ,
тоді послідовності
,
тоді послідовності
 та
та
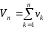 монотонно зростають та обмежені числом
монотонно зростають та обмежені числом
 ,
а тому вони збіжні, що означає збіжність
рядів
,
а тому вони збіжні, що означає збіжність
рядів
 ,
,
 .
.
Нехай тепер ряд
 збігається умовно. Якби збігалися обидва
ряди
збігається умовно. Якби збігалися обидва
ряди
 ,
,
 ,
то з рівності
,
то з рівності
 слідує абсолютна збіжність ряду
слідує абсолютна збіжність ряду
 ,
що суперечить умові. Якщо ж збігається
рівно один з двох рядів, то з рівності
,
що суперечить умові. Якщо ж збігається
рівно один з двох рядів, то з рівності
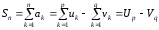 ,
де ми маємо рівність між двома збіжними
та однією розбіжною послідовностями,
що неможливо. Тому обидва ряди є розбіжними
,
де ми маємо рівність між двома збіжними
та однією розбіжною послідовностями,
що неможливо. Тому обидва ряди є розбіжними
34) Про збіжність в крузі збіжності СР поточкова та рівномірна збіжність
Нехай
 - радіус збіжності СР. Тоді СР збігається
в крузі збіжності
- радіус збіжності СР. Тоді СР збігається
в крузі збіжності
 .
Якщо
.
Якщо
 ,
то СР розбігається поточково зовні
круга збіжності, тобто в тих точках, де
,
то СР розбігається поточково зовні
круга збіжності, тобто в тих точках, де
 .
.
Нехай
 - радіус збіжності СР і
- радіус збіжності СР і
 .
Тоді СР в крузі
.
Тоді СР в крузі
 збігається рівномірно.
збігається рівномірно.
Наслiдки з теореми про нормальну збiжнiсть степеневого ряду.
35) Про збіжність в крузі збіжності СР, обмеженість та абсолютна збіжність
Нехай
 - радіус збіжності СР і
- радіус збіжності СР і
 .
Тоді
.
Тоді
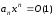 .
Якщо
.
Якщо
 ,
то
,
то

 .
.
Нехай
 - радіус збіжності СР і
- радіус збіжності СР і
 .
Тоді СР
.
Тоді СР
 - абсолютно збіжний. Якщо
- абсолютно збіжний. Якщо
 ,
то
,
то
 цей СР абсолютно розбіжний
цей СР абсолютно розбіжний
Наслiдки з теореми про нормальну збiжнiсть степеневого ряду.
36) Про монотонну обмежену послідовність
Якщо
послідовність
 монотонна й обмежена, то
монотонна й обмежена, то .
.
З теореми
Вейєрштрасса послідовність
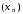 збігається, а тому збігається ряд
збігається, а тому збігається ряд
 ,
,
 ,
послідовністю часткових сум якого як
раз і є послідовність
,
послідовністю часткових сум якого як
раз і є послідовність
 .
З монотонності цієї послідовності ряд
.
З монотонності цієї послідовності ряд
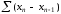 - знакосталий, а тому його збіжність
рівносильна абсолютній збіжності, що
й означає, що
- знакосталий, а тому його збіжність
рівносильна абсолютній збіжності, що
й означає, що

37) Про нормальну збіжність СР
Нехай
 - радіус збіжності СР і
- радіус збіжності СР і
 .
Тоді СР в крузі
.
Тоді СР в крузі
 збігається нормально
збігається нормально
Доведення. З означення верхньої
межі
 і при цьому
і при цьому
 .
Тоді
.
Тоді

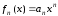

 ,
але ряд
,
але ряд
 - абсолютно збіжний, а тому і ряд
- абсолютно збіжний, а тому і ряд
 - збіжний, що й завершує доведення
теореми.
- збіжний, що й завершує доведення
теореми.
38) Про перестановку абсолютно збіжного ряду
Якщо ряд
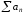 збігається абсолютно та має суму
збігається абсолютно та має суму
 ,
то будь-яка його перестановка також
збігається та має ту ж саму суму
,
то будь-яка його перестановка також
збігається та має ту ж саму суму

Доведення. Нехай
 - часткові суми перестановки ряду, а
- часткові суми перестановки ряду, а
 ,
тоді послідовність
,
тоді послідовність
 - монотонно зростає та обмежена числом
- монотонно зростає та обмежена числом
 ,
а тому ця послідовність збіжна, з чого
слідує абсолютна збіжність будь-якої
перестановки, а тому і проста її збіжність.
,
а тому ця послідовність збіжна, з чого
слідує абсолютна збіжність будь-якої
перестановки, а тому і проста її збіжність.
З критерію Коші маємо:

 :
:

 . (1)
. (1)
Нехай
 - найбільший з індексів, який мають числа
- найбільший з індексів, який мають числа
 ,
коли вони є членами перестановки
,
коли вони є членами перестановки
 .
Зрозуміло, що
.
Зрозуміло, що
 .
Розглянемо довільне
.
Розглянемо довільне
 ,
тоді в різниці
,
тоді в різниці
 ,
члени ряду з номерами від
,
члени ряду з номерами від
 до
до
 скорочуються, і залишаються лише члени
з номерами, більшими за
скорочуються, і залишаються лише члени
з номерами, більшими за
 .
Внаслідок (1)
.
Внаслідок (1)


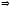
 ,
а тому
,
а тому
 ,
що й треба було довести.
,
що й треба було довести.
39) Про послідовність з обмеженою варіацією
Якщо
 ,
то
,
то

Запишемо
вказану послідовність у вигляді:
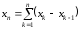 ,
,
 .
Тоді з того, що
.
Тоді з того, що
 має обмежену варіацію, слідує абсолютна
збіжність ряду
має обмежену варіацію, слідує абсолютна
збіжність ряду
 ,
а тому і просто збіжність того ж ряду,
але це означає, що збіжною є послідовність
його часткових сум, тобто послідовності
,
а тому і просто збіжність того ж ряду,
але це означає, що збіжною є послідовність
його часткових сум, тобто послідовності
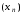
40)
Про рівнозбіжність рядів
 та …
та …
Нехай
послідовність
 не зростаюча. Тоді ряд
не зростаюча. Тоді ряд
 збіжний чи розбіжний одночасно з рядом
збіжний чи розбіжний одночасно з рядом

Розглянемо
такі позначення для часткових сум
 ,
,
 .
.
Якщо
 ,
то
,
то

 ,
а тому
,
а тому
 . (1)
. (1)
Якщо
 ,
то
,
то

 ,
тобто
,
тобто
 . (2)
. (2)
Якщо
ряд
 збіжний, то послідовність
збіжний, то послідовність
 обмежена, а тому обмеженою є також
послідовність
обмежена, а тому обмеженою є також
послідовність
 ,
що слідує з нерівності (1),
тоді
й ряд
,
що слідує з нерівності (1),
тоді
й ряд
 є збіжним. Якщо ж ряд
є збіжним. Якщо ж ряд
 розбіжний, то відповідна послідовність
часткових сум
розбіжний, то відповідна послідовність
часткових сум
 необмежена, а тому й послідовність
необмежена, а тому й послідовність
 також необмежена, що слідує з нерівності
(2).
А з останнього слідує, що ряд
також необмежена, що слідує з нерівності
(2).
А з останнього слідує, що ряд
 - розбіжний. Повністю аналогічно в
зворотному порядку.
- розбіжний. Повністю аналогічно в
зворотному порядку.


 ,
то її рівномірна границя єдина.
,
то її рівномірна границя єдина.
 збіжний, якщо
збіжний, якщо
 ,
та розбіжний якщо
,
та розбіжний якщо
 .
. не обов’язково слідує розбіжність
ряду
не обов’язково слідує розбіжність
ряду
 .
. ,
де
,
де
 ,
,
 ,
,
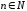 .
Легко зрозуміти, що цей ряд збіжний,
бо послідовність її часткових сум
обмежена, бо
.
Легко зрозуміти, що цей ряд збіжний,
бо послідовність її часткових сум
обмежена, бо
 ,
а тому і ряд
,
а тому і ряд
 - збіжний.
- збіжний. ,
то для непарних
,
то для непарних
 одержимо:
одержимо:
 ,
,
 ,
а тому й
,
а тому й
 .
.