
Шпаргалка ТАУ
.pdf
21
.
Передавальна функція ланки:
.
Така ланка є ідеалізацією реальних інтегруючих ланок. Приклади: операційний підсилювач в режимі
інтегрування; гідравлічний демпфер; гідравлічний серводвигун; інтегруючий привід і т.д.
 .
.
Вхідною величиною демпфера є сила F, що діє на поршень, а вихідною – переміщення поршня y. Так як швидкість руху поршня пропорційна прикладеній силі
(без врахування інерційних сил) |
, де S – |
коефіцієнт швидкісного опору, то переміщення |
|
.
Часові характеристики:
–перехідна характеристика h(t)=kt∙1(t)
–імпульсна перехідна характеристика  ∙1(t)
∙1(t)
Частотні характеристики
Логарифмічна амплітудна і фазова частотні характеристики.
Амплітудна фазова характеристика для додатних частот співпадає з від’ємною частиною уявної осі.
Амплітудна частотна характеристика показує, що ланка пропускає сигнал тим сильніше, чим менше його частота. При =0 А( ) , а при 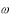 А( ) 0.
А( ) 0.
ЛАХ будується по виразу
.
ЛАХ є прямою лінією з від’ємним нахилом 20дБ/дек, яка перетинає вість абсцис при частоті зрізу зр=k. ЛФХ є прямою лінією =-90 , паралельною осі частот.
7. Інтегруюча ланка з сповільненням.
Диференціальне рівняння
.
Передавальна функція
.
До такого типу ланок відносяться той самий демпфер, серводвигун, інтегруючий привід, якщо більш точно розглядати їх рівняння руху.
Інтегруючу ланку з сповільненням також можна представити як сукупність двох послідовно включених ланок – ідеальної інтегруючої і аперіодичної першого порядку.
Для одержання часових характеристик зручно передаточну функцію записати у вигляді алгебраїчної
суми , що дозволяє представити розв’язок диференціального рівняння у вигляді суми розв’язків для ідеальної інтегруючої ланки і аперіодичної ланки першого порядку.
Часові характеристики.
Перехідна функція. Та сама характеристика, що для ідеальної інтегруючої ланки, тільки зміщена на деяку величину.
Імпульсна перехідна характеристика.
Частотні характеристики.
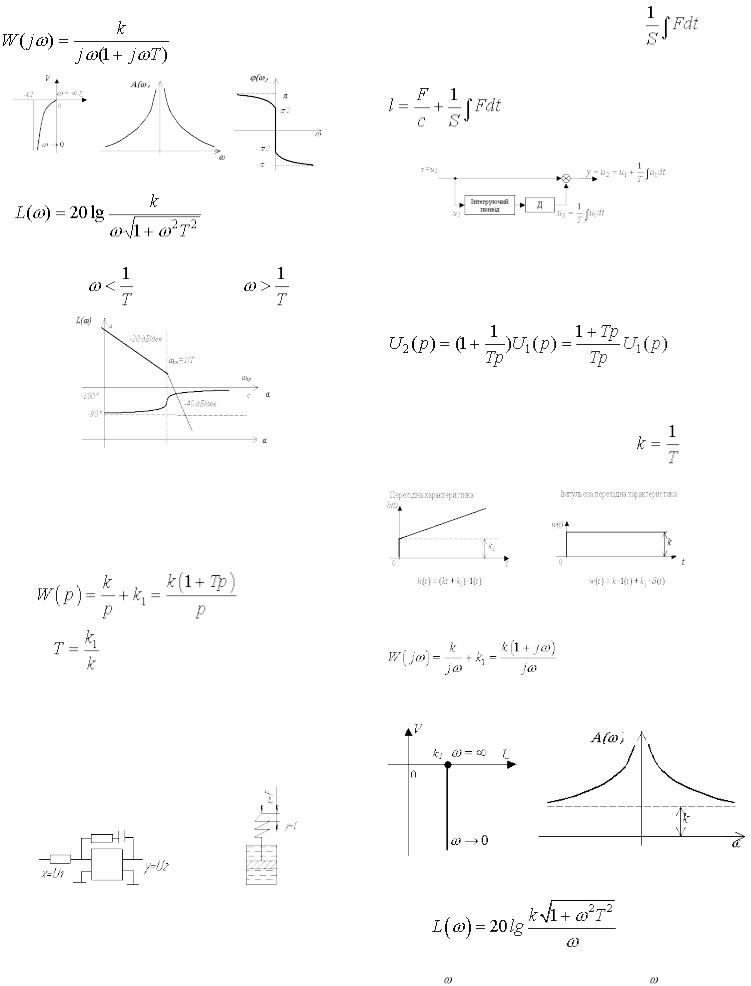
22
Частотна передавальна функція
.
ЛАХ будується по виразу
.
Асимптотична ЛАХ – це дві прямі з від’ємним нахилом
20 дБ/дек (при |
) і 40 дБ/дек (при |
). |
8. Ізодромна ланка.
Диференціальне рівняння
 .
.
Передавальна функція:
|
, |
де |
- постійна часу ізодромної ланки. |
Ізодромну ланку можна умовно представити у вигляді двох ланок, що діють паралельно – ідеальної інтегруючої з коефіцієнтом передачі k і без інерційної з коефіцієнтом передачі k1.
Прикладами є: операційний підсилювач з RCелементами в зворотному зв’язку; комбінація пружини з демпфером, ізодромна ланка на базі інтегруючого приводу.
жорсткість пружини, і переміщення поршня |
, де |
S – коефіцієнт швидкісного опору демпфера. |
|
Результуюче переміщення точки |
|
.
Випадок ізодромної ланки на базі інтегруючого пристрою:
Вхідна напруга u1подається безпосередньо на вихід. Крім того ця ж дія u1 подається на вхід інтегруючого приводу. Кут повороту валика інтегруючого приводу пропорційний інтегралу вхідного сигналу u1. Д – давач (потенціометр або обертовий лінійний трансформатор), що перетворює кут повороту в напругу u3. u3 сумується з u1:
,
де Т – коефіцієнт пропорційності між швидкістю зміни вихідної напруги давача інтегрального приводу і напругою на його вході. Коефіцієнт передачі ідеальної
інтегруючої ланки в цьому випадку рівний |
. |
Часові характеристики. |
|
Частотні характеристики. Амплітудно фазова частотна функція:
=  ,
,
T=k1/k.
Вхідна величина для демпфера – сила F, а вихідна – переміщення l точки, в якій прикладена сила. Це переміщення складається з деформації пружини F/c, де с –
Логарифмічна амплітудна характеристикабудується згідно
виразу . Асимптотична ЛАХ – дві прямі: з від’ємним нахилом 20 дБ/дек (при <1/Т) і паралельна осі частот (при >1/Т).

23
З ЛАХ і ЛФК видно, що в області малих частот ланка веде себе як ідеальна інтегруюча.
В області великих частот (більші, як спряжена частота) ланка веде себе як без інерційна з коефіцієнтом передачі
k1.
Властивість ланки вводити інтегруючу дію в область малих частот використовують для покращення якісних показників САК.
9. Ідеальна диференціююча ланка.
Диференціальне рівняння
. |
|
Передавальна функція |
. |
Приклади: тахогенератор постійного стуму, якщо в якості
вхідної величини розглядати кут повороту ротора х=  , а в якості вихідної у=е – е.р.с. якоря.
, а в якості вихідної у=е – е.р.с. якоря.
Логарифмічна частотна функція:
.
10. Диференціююча ланка з сповільненням.
Диференціальне рівняння
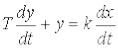 ,
,
Передавальна функція в операторній формі:
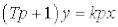 .
.
.
Умовно ланку можна представити як послідовне включення двох ланок – ідеальної диференціюючої і аперіодичної першого порядку.
Прикладами є RC-ланка,RL- ланка, трансформатор напруги (х=U1, y=U2).
Часові харак
В тахогенераторі |
. Швидкість обертів |
, тому |
. В режимі холостого ходу |
і |
. |
В деякому наближенні операційний підсилювач можна розглядати в якості ідеальної диференціальної ланки: Часові характеристики.
Частотні характеристики. Амплітудно фазова частотна функція:
 .
.
теристики.
Частотні характеристики. Частотна передавальна функція
та
характеристика.
24
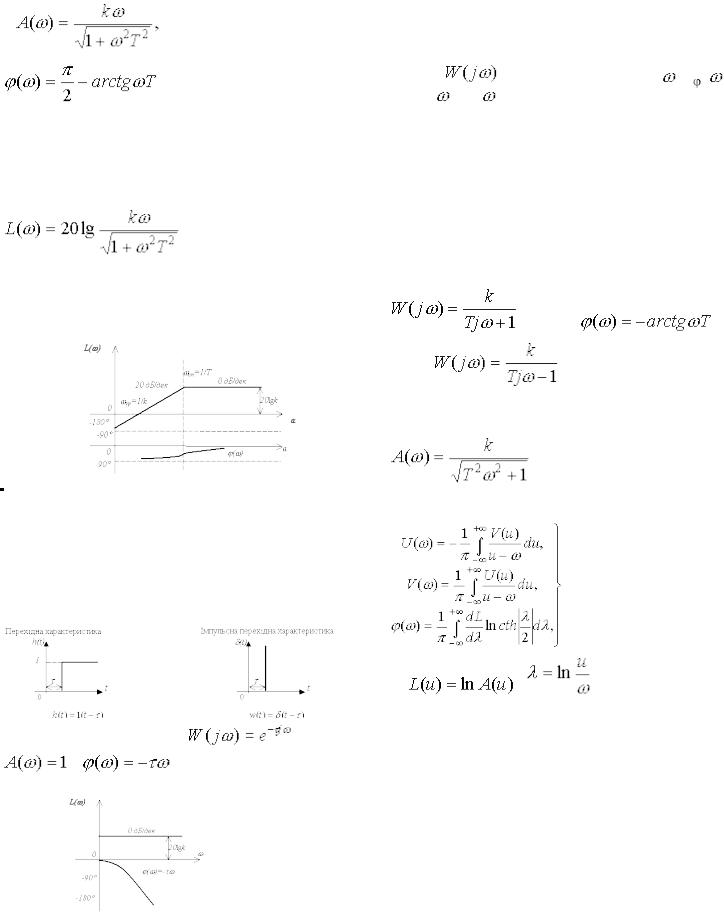
Амплітудна і фазова частотні характеристики
АЧХ має інший вигляд, ніж у ідеальної ланки. Характеристики співпадають в області низьких частот. В області високих частот реальна ланка пропускає сигнал гірше, ніж ідеальна. Фазові зсуви найбільші при низьких
частотах. На високих частотах 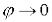 при
при  . ЛАХ будують згідно виразу
. ЛАХ будують згідно виразу
.
Асимптотичну ЛАХ представляють у вигляді двох прямих. Одна із них має додатній нахил 20 дб/дек (при
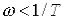 ), а друга – паралельна осі частот (при
), а друга – паралельна осі частот (при
 ).
).
11. Ланка з постійним запізненням.
Рівняння ланки
 ,
,
 при
при 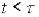 ,
, 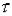 – час запізнення.
– час запізнення.
Передавальна функція ланки 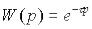 . Часові характеристики.
. Часові характеристики.
Частотна передавальна функція |
; |
|
; |
. |
|
Логариф |
|
|
мічні частотні характеристики:
Диференціальне рівняння в операторній формі:
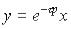 .
.
12. Мінімально-фазові ланки та системи.
Щоб повністю описати ланку або систему в загальному випадку необхідно знати їх частотну передавальну
функцію |
або любу пару функцій: А( ) і ( |
) або U( )і V( |
). |
Для деякого класу ланок та систем частотна передавальна функція повністю визначається однією із функцій:
модулем А( 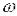 ), дійсною частиною U(
), дійсною частиною U( 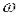 ) або уявною
) або уявною
частиною V(  ). Такі ланки називають мінімальнофазовими (або стійкими) – це ланки, корені чисельника і знаменника передавальної функції яких мають від’ємні дійсні частини. Мінімально-фазові ланки мають менші по абсолютній величині фазові зсуви в порівнянні із ланками, в яких ці умови не виконуються.
). Такі ланки називають мінімальнофазовими (або стійкими) – це ланки, корені чисельника і знаменника передавальної функції яких мають від’ємні дійсні частини. Мінімально-фазові ланки мають менші по абсолютній величині фазові зсуви в порівнянні із ланками, в яких ці умови не виконуються.
Наприклад: аперіодична ланка першого порядку (мінімально-фазова):
, для якої
і ланка |
(не мінімально-фазова), для |
якої 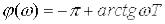 . Слід зауважити, що модулі обох ланок однакові і рівні
. Слід зауважити, що модулі обох ланок однакові і рівні
.
Для мінімально-фазових ланок справедливі наступні вирази:
де |
, |
, а и – змінна |
інтегрування. |
|
|
13. Нестійкі ланки.
Всі розглянуті вище ланки, крім інтегруючої, є стійкими, так як полюси їх передавальних функцій мають від’ємні дійсні частини. Вони є також, крім ланки з постійним запізненням, і мінімально-фазовими, так як їх передавальні функції не мають ще й нулів з додатною дійсною частиною.
Стійкими є такі ланки або системи, які мають властивість самі переходити до нового усталеного значення, при необмеженій зміні вхідної величини або збурюючій дії. Перехідні характеристики нелінійних ланок необмежено зростають в часі.
Нестійкими є всі ланки, передавальні функції яких відрізняються від передавальних функцій розглянутих

25
перед цим основних ланок, зміною знаку будь-якого із членів знаменника на від’ємний:
Тема IV. Передавальні функції та структурні схеми САК.
1.Одержання передавальних функцій системи по передавальних функціях ланок.
а) передавальні функції послідовно з’єднаних ланок; б) передавальні функції паралельно з’єднаних ланок; в) ланка, охоплена зворотнім зв’язком.
2.Правила переносу вхідних і вихідних сигналів ланок в структурних схемах.
3.Формула Мейсона.
4.Побудова частотних характеристик систем по частотних характеристиках ланок.
1. Одержання передавальних функцій системи по передавальних функціях ланок.
а) передавальні функції послідовно з’єднаних ланок
, |
, …, |
 .
.
Очевидно, що 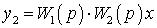 ,
,
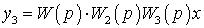 , … .
, … .
Звідки,
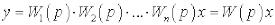 ,
,
або
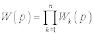 .
.
Отже, передавальна функція всієї системи послідовно з’єднаних ланок дорівнює добутку передавальних функцій ланок.
б) передавальна функція паралельно з’єднаних ланок напрямленої дії.
Якщо |
, |
, |
 то
то
=W(p)х,
де |
. |
|
Отже, передавальна функція групи паралельно |
з’єднаних ланок дорівнює сумі передавальних функцій окремих ланок.
в) ланка, охоплена зворотнім зв’язком
х33 –сигнал зворотного зв’язку.
.
„–” відповідає додатному зворотному зв’язку; „+” відповідає від’ємному зворотному зв’язку. Виключаючи х33, отримуємо
,
або
|
х, |
де |
|
|
– передавальна функція |
замкнутого кола, |
|
а |
– передавальна функція |
розімкнутого кола.
Знак „–” відповідає додатному зворотному зв’язку, а знак „+” відповідає від’ємному зворотному зв’язку.
Приклад:
Загальний зворотній зв’язок в САУ завжди має знак «–».
Знайти:  ,
,  ,
,
.
,
звідки
,
де |
= |
, а |
.
,

26
де |
. |
|
В САР часто як контрольовану вихідну величину |
|
|
розглядають крім x(y) ще й помилку |
|
|
– помилку розузгодження. |
|
|
і |
|
|
|
. |
|
При одночасній дії f іxз |
|
|
|
. |
|
2. Правила переносу вхідних і вихідних сигналів в |
|
|
структурних схемах. |
|
|
Перенесення елементу сумування: |
|
|
|
–> |
. |
|
або |
|
де 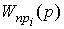 – передавальні функції окремих прямих шляхів від входу до виходу системи, тобто від вхідної дії до вихідної величини;
– передавальні функції окремих прямих шляхів від входу до виходу системи, тобто від вхідної дії до вихідної величини;
, |
|
де |
– сума передавальних функцій всіх |
контурів; |
|
 і
і 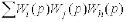 – суми добутків двох, трьох і т.д. передавальних функцій контурів, що не стикаються між собою;
– суми добутків двох, трьох і т.д. передавальних функцій контурів, що не стикаються між собою;
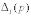 – це
– це 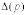 після вилучення і-го прямого шляху (при цьому пропадають і паралельні інші шляхи, які починаються або закінчуються в спільних із цим шляхом точках).
після вилучення і-го прямого шляху (при цьому пропадають і паралельні інші шляхи, які починаються або закінчуються в спільних із цим шляхом точках).
.
Перенесення точки розгалуження:
після:
або .
4. Побудова частотних характеристик по частотним характеристикам ланок.
Зв’язок між частотними функціями системи і ланок, що входять в систему, визначаються виразом для передавальної функції, якщо підставити вираз p=j . Відповідно, амплітудна фазова частотна функція групи послідовно з’єднаних ланок розімкнутої системи рівна:
 , де
, де 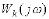 – амплітудна фазова частотна функція k-ї ланки.
– амплітудна фазова частотна функція k-ї ланки.
Приклади перетворення структурних схем:
3. Формула Мейсона.
,
Звідки, |
, тобто |
 ,
,
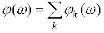 , де
, де 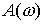 і
і 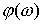 – амплітудна і
– амплітудна і
фазова функції групи ланок, а 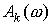 і
і 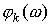 – відповідні функції k-ї ланки.
– відповідні функції k-ї ланки.
Логарифмування амплітудної функції дає вираз для ЛАХ групи послідовно з’єднаних ланок:
 , де
, де 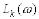 – ЛАХ окремої ланки.
– ЛАХ окремої ланки.
З цих виразів видно, що ЛАХ і ЛФХ групи послідовно з’єднаних ланок одержують шляхом сумування ординат характеристик окремих ланок.
Для прикладу, розглянемо побудову ЛАХ і ЛФХ групи послідовно з’єднаних однієї інтегруючої і двох аперіодичних ланок першого порядку.
ЛАХ групи ланок будуємо без побудови ЛАХ окремих ланок.

27
Спочатку відкладаємо ординату спільної ЛАХ при 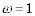 , рівну 20lgk, де k– коефіцієнт передачі всієї групи елементів (k1k2 k3=k). Потім через отриману точку проводиться асимптота з нахилом 20(m–r)дб/дек, де m – число диференціюючих ланок, r– число інтегруючих ланок. Потім, на осі абсцис відкладаємо значення спряжених частот, рівних 1/Тk, де Тk – постійна часу ланок. Далі, перша асимптота проводиться від осі ординат до найменшої спряженої частоти. В точці їх перетину знаходиться злам характеристики із зміною нахилу у відповідності із типом ланки, якій належить дана спряжена частота. Таким же чином характеристика продовжується в сторону збільшення частоти, послідовно змінюючи нахил в кожній спряженій частоті.
, рівну 20lgk, де k– коефіцієнт передачі всієї групи елементів (k1k2 k3=k). Потім через отриману точку проводиться асимптота з нахилом 20(m–r)дб/дек, де m – число диференціюючих ланок, r– число інтегруючих ланок. Потім, на осі абсцис відкладаємо значення спряжених частот, рівних 1/Тk, де Тk – постійна часу ланок. Далі, перша асимптота проводиться від осі ординат до найменшої спряженої частоти. В точці їх перетину знаходиться злам характеристики із зміною нахилу у відповідності із типом ланки, якій належить дана спряжена частота. Таким же чином характеристика продовжується в сторону збільшення частоти, послідовно змінюючи нахил в кожній спряженій частоті.
Ординати ЛФХ ланок додаються звичайним способом. В результаті граничне значення ланок, що отримується при
 , буде рівне (n–m)∙ /2, де n – порядок диференціального рівняння групи ланок, а m– число ідеальних диференціюючи ланок.
, буде рівне (n–m)∙ /2, де n – порядок диференціального рівняння групи ланок, а m– число ідеальних диференціюючи ланок.
Побудова АФХ групи послідовно з’єднаних ланок безпосередньо по АФХ окремих ланок здійснюється згідно із виразами:
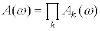 і
і 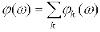 .
.
АФХ групи паралельно з’єднаних ланок дорівнює
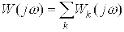 . Відповідно частотна характеристика будується шляхом геометричного сумування векторів
. Відповідно частотна характеристика будується шляхом геометричного сумування векторів
 при однакових частотах.
при однакових частотах.
Амплітудна фазова функція ланки із зворотнім зв’язком рівна
.
АЧХ і ФЧХ будують згідно виразів:
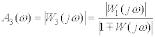 ;
;
 .
.
Логарифмічні частотні характеристики ланки із зворотнім зв’язком будують використовуючи номограми, які дозволяють по відомих логарифмічних характеристиках
розімкнутого кола 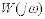 отримати логарифмічні характеристики замкнутого контуру
отримати логарифмічні характеристики замкнутого контуру 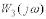 , коли
, коли
, тобто коли 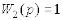 і зворотний
і зворотний
зв’язок від’ємний.
Щоб використати номограми для довільної функції
,
де до вигляду
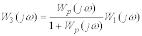 ,
,
де 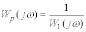 .
.
По номограмі знаходять логарифмічні характеристики для виразу в квадратних дужках. Тоді по цих характеристиках
і характеристиках, що відповідають 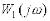 , знаходять характеристики системи, як у випадку послідовного з’єднання ланок.
, знаходять характеристики системи, як у випадку послідовного з’єднання ланок.
