
Шпаргалка ТАУ
.pdf
11
Таким чином, перехідні і частотні характеристики однозначно зв’язані з рівняннями ланок і описують їх динамічні характеристики.
Перехідні (часові) характеристики.
Перехідна або часова характеристика ланки це графік зміни в часі вихідної величини, коли на вхід ланки подається одинична (сходинкова) дія.
Одинична дія – це дія, яка миттєво зростає від нуля до одиниці і далі залишається сталою.
На рисунку показано різні види перехідних характеристик для різних ланок.
Аналітичний вираз перехідної характеристики – перехідна функція – позначається h(t).
Аналітичний вираз одиничної дії позначається 1(t) і описується як система
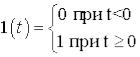 .
.
Таким чином, h(t) це вираз для y(t) при x(t)=1(t).
Якщо вхідна величина є неодиничною сходинковою функцією x(t)=N×1(t), то вихідна величина рівна y(t)=N×h(t).
Сходинкова функція є розповсюдженим видом вхідної дії в автоматичних системах. До такого виду дій відносяться: миттєва зміна навантаження електричного генератора, миттєва зміна навантаження на валу двигуна, миттєвий поворот вала слідкуючої системи і т.п.
Також в ТАУ використовують поняття імпульсної перехідної характеристики – це реакція ланки або системи на одиничний імпульс.
Одиничний імпульс – це математична ідеалізація гранично короткого імпульсу. Це імпульс, площа якого рівна одиниці при тривалості що рівна нулю і висоті що рівна нескінченності.
На рисунку показано типові форми імпульсних перехідних характеристик
Аналітичним виразом для імпульсної перехідної характеристики є імпульсна перехідна функція, або функція ваги, яка позначається w(t). Вираз для одиничного імпульса називається одиничною імпульсною функцією або дельта-функцією і позначається d(t). Таким чином, w(t)
– це y(t) при x(t)=d (t).
Математично дельта-функція записується як
При цьому, |
. |
Дельта-функція пов’язана з одиничною сходинковою функцією співвідношенням 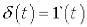 .
.
А перехідна і вагова функція співвідносяться як
і |
. |
Перетворення Лапласа імпульсної і перехідної функції мають вигляд:
, |
, |
а
, |
, |
. |
Імпульсна функція також є розповсюдженим видом вхідної дії в автоматичних системах. До такого виду відносять: короткочасний удар навантаження на валу

12
двигуна, короткочасний струм короткого замикання генератора і т.п.
Знаючи перехідну або вагову функцію можна визначити реакцію ланки на довільну вхідну дію, при нульових початкових умовах, за формулами:
, |
(1) |
де 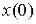 – значення
– значення 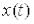 при t=0;
при t=0;
. |
(2) |
На рисунку дано геометричну інтерпретацію виразу (1). Тут реакція y(t) на довільну дію х(t) визначена як границя
суми реакцій на сходинкові дії висотою 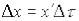 , на які можна розкласти
, на які можна розкласти 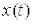 , при
, при 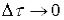 .
.
Вирази (1) і (2) є варіантами інтеграла Дюамеля, або інтегралу згортки.
8. Частотні характеристики, частотні функції.
Частотні характеристики описують усталені вимушені коливання на виході ланки, які викликані гармонічною дією на вході.
Нахай на вхід ланки подається гармонічний сигнал (дія)
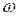 – кутова частота.
– кутова частота.
Після закінчення перехідного процесу, на виході гармонічні коливання мають вигляд y=Ymsin( 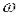 t+
t+ 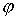 ), де
), де
Ym– амплітуда вихідного сигналу усталених коливань;
– фазовий зсув між вхідними і вихідними коливаннями.
При фіксованій амплітуді вхідних коливань, амплітуда Ymі фаза  усталених коливань на виході ланки залежать від частоти
усталених коливань на виході ланки залежать від частоти  . Якщо збільшувати частоту
. Якщо збільшувати частоту 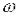 від 0 і визначати Ymі
від 0 і визначати Ymі 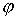 , то можна одержати залежність від
, то можна одержати залежність від
частоти відношення амплітуд |
і зсуву фаз |
вихідних і вхідних усталених коливань. |
|
Залежність від частоти відношенням амплітуд вихідних
і вхідних усталених коливань А( 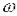 ) називається амплітудною частотною характеристикою (АЧХ).
) називається амплітудною частотною характеристикою (АЧХ).
Залежність від частоти зсуву фаз вихідних і вхідних
усталених коливань 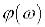 називають фазовою частотною характеристикою (ФЧХ).
називають фазовою частотною характеристикою (ФЧХ).
В силу інерційності, АЧХ при  спадає до нуля. Чим менш інерційна ланка, тим ширша її АЧХ, тобто більша полоса (смуга) пропускання частот ланки.
спадає до нуля. Чим менш інерційна ланка, тим ширша її АЧХ, тобто більша полоса (смуга) пропускання частот ланки.
Практично полоса пропускання оцінюється значенням частоти, при якій відношення амплітуд стає меншим певного достатньо малого кінцевого значення. Зазвичай, це значення приймають рівним 0,05% (тобто Ymстановить 5% від Хm). Наявність максимуму АЧХ говорить про резонансні властивості ланки. Частота, яка відповідає максимуму АЧХ називається резонансною частотою.
Фазова характеристика у звичайних інерційних ланок
від’ємна (  <0), тобто вихідні коливання відстають по фазі від вхідних і це відставання зростає із частотою.
<0), тобто вихідні коливання відстають по фазі від вхідних і це відставання зростає із частотою.
Амплітудна і фазова частотні характеристики можуть бути об’єднані в одну характеристику – амплітудно-фазову
частотну характеристику (АФЧХ), використовуючи А( 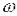 ) і
) і
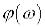 в якості полярних координат.
в якості полярних координат.
Кожна точка АФЧХ відповідає певному значенню 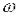 . По АФЧХ можна побудувати як АЧХ А(
. По АФЧХ можна побудувати як АЧХ А( 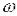 ), так і ФЧХ
), так і ФЧХ

13
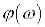 . АФЧХ можна також побудувати і в прямокутній системі координат – в комплексній площині. Проекції вектора Аі на осі координат позначають U і V і називають
. АФЧХ можна також побудувати і в прямокутній системі координат – в комплексній площині. Проекції вектора Аі на осі координат позначають U і V і називають
відповідно дійсною 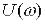 і уявною
і уявною 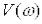 частотними характеристиками.
частотними характеристиками.
Аналітичні вирази для розглянутих вище частотних характеристик можуть бути одержані по передавальній функції наступним чином. Якщо в вираз W(p) підставити р=j
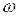 , то одержана комплексна величина W(j
, то одержана комплексна величина W(j 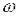 ), яка є комплексною функцією, і називається амплітудно-фазовою частотною характеристикою. Ця функція є аналітичним виразом АФЧХ. Її модуль є виразом для амплітудної частотної характеристики – амплітудна частотна функція А(
), яка є комплексною функцією, і називається амплітудно-фазовою частотною характеристикою. Ця функція є аналітичним виразом АФЧХ. Її модуль є виразом для амплітудної частотної характеристики – амплітудна частотна функція А(
 ), а аргумент є виразом для фазової частотної
), а аргумент є виразом для фазової частотної
характеристики – фазова частотна функція 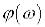 . Доведемо це.
. Доведемо це.
Використаємо формулу Ейлера і представимо вхідну і вихідну гармонічні дії у вигляді:
,
.
В лінійних системах на основі принципу суперпозицій можна розглянути окремо проходження 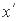 і
і 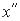 .
.
Достатньо розглянути 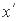 , який на виході дає обумовлює складову
, який на виході дає обумовлює складову 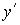 . Співвідношення між
. Співвідношення між 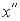 і
і 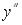 таке саме,
таке саме,
як і між 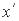 і
і 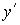 . Тому, далі будемо використовувати символічний запис
. Тому, далі будемо використовувати символічний запис 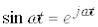 . Тоді,
. Тоді,
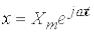 ,
,
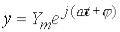 .
.
Рівняння ланки в загальному можна записати у вигляді
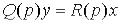 .
.
В це рівняння підставимо значення 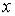 і
і  в символьному записі, при цьому врахуємо, що
в символьному записі, при цьому врахуємо, що
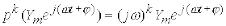 ,
,
.
Звідси,
.
Але |
, а |
. |
Тому, 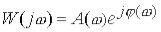 .
.
В алгебраїчній формі 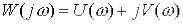 ,
,
де 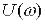 і
і 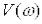 – відповідно дійсна і уявна частотні функції.
– відповідно дійсна і уявна частотні функції.
Зв’язок між частотними функціями
,
,
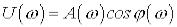 ,
,
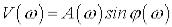 .
.
Порядок одержання частотних характеристик по
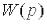 :
:
;
,
де |
, |
 ,
,
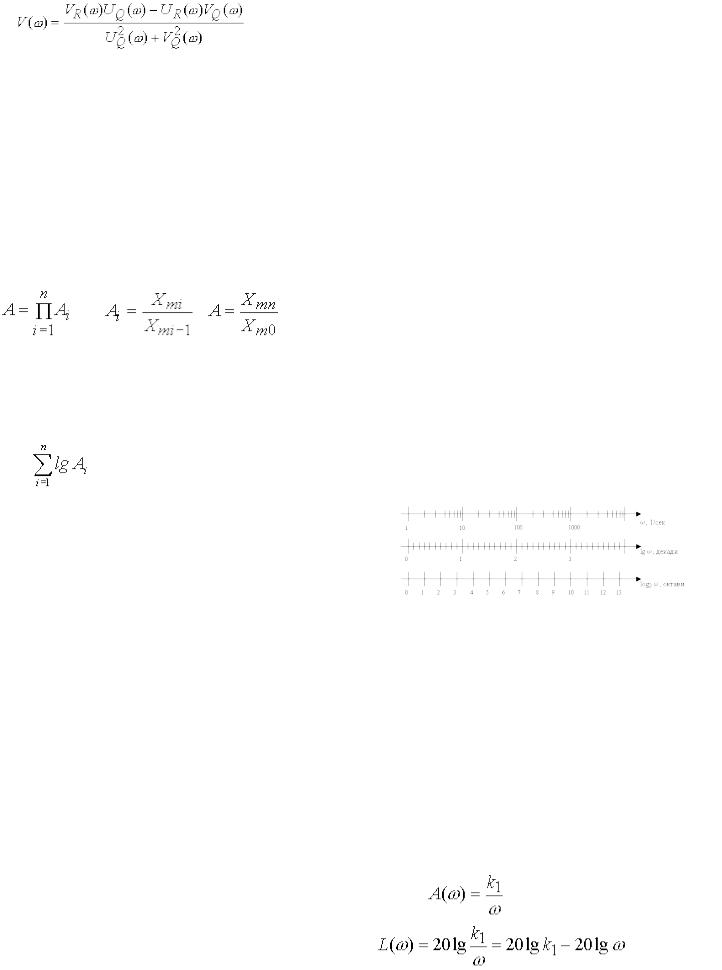
14
.
9. Логарифмічні частотні характеристики.
Під час дослідження САК амплітудну і фазову частотні характеристики зручно будувати в логарифмічних координатах. Це зручно з двох обставин. По-перше, так як в логарифмічних координатах є можливість в більшості практичних випадків спрощено зображати амплітудні частотні характеристики ламаною лінією.
Друга зручність пов’язана з побудовою амплітудних характеристик послідовно-з’єднаних ланок. АЧХ послідовно з’єднаних ланок рівна
, де |
, |
, де |
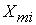 і
і  – амплітуди коливань на вході і виході і-ї ланки.
– амплітуди коливань на вході і виході і-ї ланки.
Якщо прологарифмувати вираз для А, то одержимо
lgA= .
Тобто, в логарифмічному масштабі амплітудна частотна функція послідовно з’єднаних ланок рівна сумі амплітудних частотних функцій окремих ланок.
Амплітудна частотна характеристика, побудована в логарифм координатах у вигляді залежності 20 lgА( 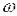 )
)
від lg  називається логарифмічною амплітудною характеристикою (ЛАХ). А фазова частотна
називається логарифмічною амплітудною характеристикою (ЛАХ). А фазова частотна
характеристика, побудована у вигляді залежності 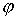 від
від
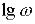 , називається логарифмічною фазовою характеристикою (ЛФХ).
, називається логарифмічною фазовою характеристикою (ЛФХ).
Величина 20 lgА( 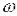 ) позначається
) позначається 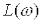 і рівна
і рівна
 . Одиниця вимірювання
. Одиниця вимірювання
ЛАХ  – децибел, який рівний 1/10 бела. А Бел – це одиниця вимірювання десяткового логарифма коефіцієнта підсилення потужності сигналу, тобто 1 Бел відповідає підсилення потужності в 10 раз, 2 бела – в 100 раз і т.д. Так як потужність сигналу пропорційна квадрату
– децибел, який рівний 1/10 бела. А Бел – це одиниця вимірювання десяткового логарифма коефіцієнта підсилення потужності сигналу, тобто 1 Бел відповідає підсилення потужності в 10 раз, 2 бела – в 100 раз і т.д. Так як потужність сигналу пропорційна квадрату
амплітуди, а 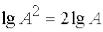 , то підсилення в белах, що виражається через відношення амплітуд A, рівне 2lgA. Відповідно в децибелах підсилення рівне 20 lgA. Один
, то підсилення в белах, що виражається через відношення амплітуд A, рівне 2lgA. Відповідно в децибелах підсилення рівне 20 lgA. Один
децибел відповідає зміні амплітуди в 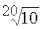 раз, тобто є відносно малою величиною (1,122…).
раз, тобто є відносно малою величиною (1,122…).
Між значеннями А і L існують наступні співвідношення:
А |
0,0 |
0,0 |
0, |
0,3 |
0,8 |
1 |
1,1 |
3,1 |
1 |
10 |
100 |
|
01 |
1 |
1 |
16 |
9 |
|
2 |
6 |
0 |
0 |
0 |
L, |
-60 |
- |
- |
-10 |
-1 |
0 |
1 |
10 |
2 |
40 |
60 |
д |
|
40 |
2 |
|
|
|
|
|
0 |
|
|
Б |
|
|
0 |
|
|
|
|
|
|
|
|
Для побудови логарифмічної фазової характеристики
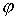 від
від 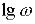 використовується та сама вісь абсцис, що і для ЛАХ. На осі абсцис вказують або прямо значення
використовується та сама вісь абсцис, що і для ЛАХ. На осі абсцис вказують або прямо значення
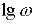 , або, що практично більш зручно, значення самої частоти
, або, що практично більш зручно, значення самої частоти 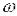 . В першому випадку, одиницею приросту
. В першому випадку, одиницею приросту
 є декада, що відповідає зміні частоти в 10 раз. Використовують також поділ осі абсцис на октави. Октава відповідає зміні частоти в два рази.
є декада, що відповідає зміні частоти в 10 раз. Використовують також поділ осі абсцис на октави. Октава відповідає зміні частоти в два рази.
w |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
|
|
|
|
|
|
|
|
|
|
0 |
L |
0 |
0.3 |
0.4 |
0.6 |
0.6 |
0.7 |
0.8 |
0.9 |
0.9 |
1 |
g |
|
01 |
77 |
22 |
99 |
78 |
15 |
02 |
54 |
|
w |
|
|
|
|
|
|
|
|
|
|
Головною позитивною якістю ЛАХ є можливість побудови її б багатьох випадках, практично без обчислень. Якщо передаточна функція є добутком передаточних функцій ланок, то результуючу ЛАХ можна представити як суму ординат ЛАХ, що відповідають окремим множникам. Часто непотрібно навіть такого сумування і результуючу ЛАХ будують у вигляді асимптотичної ЛАХ, яка являє собою сукупність відрізків прямих ліній з нахилом, що кратний 20 дБ/дек.
Приклад 1.
Нехай А( 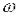 )=k0. Тоді,
)=k0. Тоді,
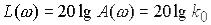 . ЛАХ – пряма лінія, паралельна осі абсцис. Приклад 2.
. ЛАХ – пряма лінія, паралельна осі абсцис. Приклад 2.
Нехай |
. Тоді |
. Якщо 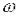 =1
=1

15
сек-1, то 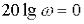 і
і  . Неважко бачити, що
. Неважко бачити, що 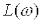 – пряма лінія, яка проходить через
– пряма лінія, яка проходить через
точку 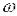 =1 сек-1 і
=1 сек-1 і 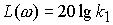 і має від’ємний нахил 20 дБ/дек, так як кожне збільшення частоти в 10 раз
і має від’ємний нахил 20 дБ/дек, так як кожне збільшення частоти в 10 раз
викличе збільшення  на одну одиницю, тобто
на одну одиницю, тобто
зменшення 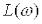 на 20 дБ.
на 20 дБ.
Тема ІІІ. Типові ланки систем автоматичного керування.
1.Безінерційна ланка.
2.Аперіодична ланка першого порядку.
3.Аперіодична ланка другого порядку.
4.Коливна ланка.
5.Консервативна ланка.
6.Інтегруюча ланка.
7.Інтегруюча ланка із сповільненням.
8.Ізодромна ланка.
9.Ідеальна диференціююча ланка.
10.Диференціююча ланка із сповільненням.
11.Ланка з постійним запізненням.
12.Мінімально-фазові ланки та системи.
13.Нестійкі ланки.
1. Безінерційна ланка (статична ідеальна ланка).
Описується рівнянням y=kx. Передавальна функція
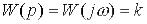 .
.
Прикладами таких ланок є механічний редуктор (без врахування скручування і люфту, безінерційний (широкополосний) підсилювач, подільник напруги і т.п. Різноманітні давачі: індукційний давач, потенціометричний давав, обертовий трансформатор.
Перехідна функція – сходинкова функція – при
 .
.
Функція ваги – імпульсна функція, площа якої рівна k,
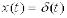
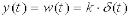 .
.
АФЧХ вироджується в точку.
Модуль частотної передавальної функції
постійний на всіх частотах, а фазові зсуви рівні 0 (
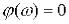 )
)
Безінерційна ланка є деякою ідеалізацією реальних ланок. В дійсності немає таких ланок, що рівномірно
пропускають всі частоти від 0 до 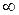 .
.
1. Аперіодична ланка першого порядку.
Описується рівнянням
(1)
Передавальна функція
.
Прикладами є:
1) – двигуни будь-якого виду (електричні, пневматичні, гідравлічні, механічні і т.д.), механічні характеристики яких представлені паралельними прямими. Вхідна величина х тут є керуючою дією в двигуні, наприклад напруги в електричному двигуні, розхід рідини в гідравлічному і т.п. Вихідною величиною є швидкість
обертів 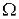 .
.
Диференціальне рівняння руху при рівному нулю моменту навантаження записується у вигляді
,
де 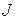 – приведений до вала двигуна сумарний момент інерції,
– приведений до вала двигуна сумарний момент інерції, 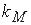 – коефіцієнт пропорційності між керуючою
– коефіцієнт пропорційності між керуючою
дією х і обертовим моментом, – нахил механічної, рівний відношенню пускового моменту до швидкості холостого ходу при деякому значенні керуючої дії.
Рівняння зводиться до вигляду
,
де |
– коефіцієнт передачі ланки, |
–постійна часу двигуна.
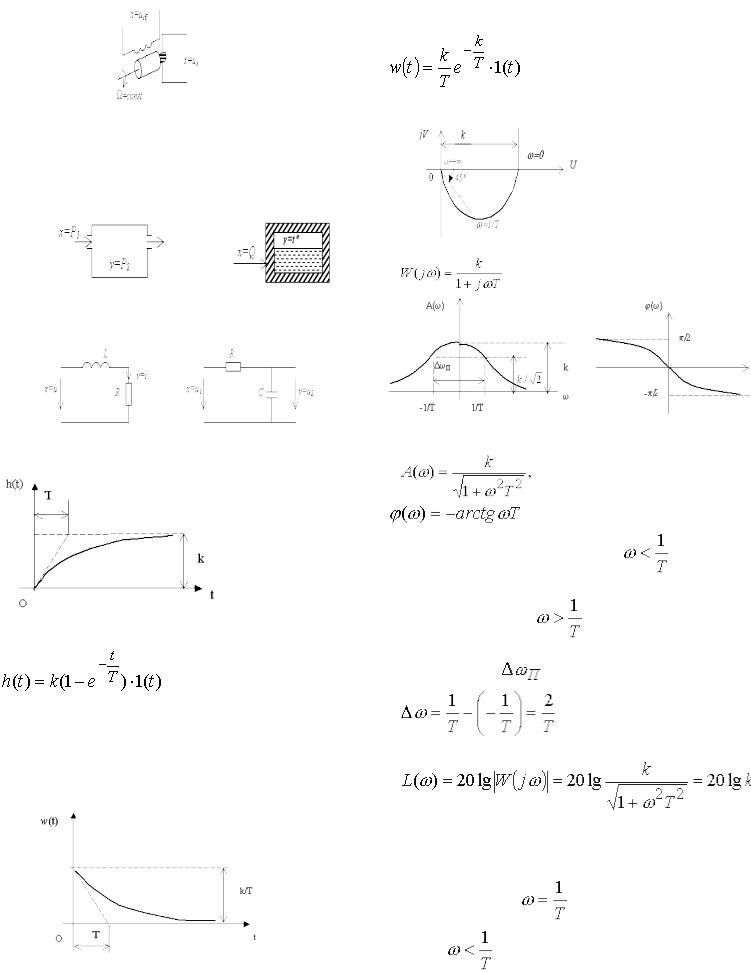
2)– другий приклад – електричний генератор постійного струму, вхідною величиною якого є напруга
збудження 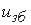 , а вихідною – напруга якоря
, а вихідною – напруга якоря  .
.
16
3)– аперіодичною ланкою першого порядку є також
резервуар з газом (у якого вхідною величиною є тиск Р1 перед впускним отвором, а вихідною – тиск Р2 в резервуарі) і нагрівна піч (вхідна величина Q – кількість тепла, що поступає, за одиницю часу, а вихідна – температура в печі).
4)– електричні RCіLR- кола, в відповідності із наступними схемами
Для всіх вищевказаних прикладів диференціальне рівняння має вигляд рівняння (1).
Перехідна функція – експонента
Чим більше Т, тим довше триває перехідний процес.
Практично 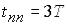 , інколи
, інколи 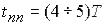 . Постійна часу характеризує «інерційність», або «інерційне запізнення», аперіодичної ланки. Вихідне
. Постійна часу характеризує «інерційність», або «інерційне запізнення», аперіодичної ланки. Вихідне
значення y=kx в аперіодичній ланці встановлюється тільки через деякий час  після подачі вхідної дії.
після подачі вхідної дії.
Функція ваги w(t) визначається диференціюванням h(t) –
Амплітудно-фазова частотна характеристика для додатних частот – півколо з діаметром k.
Частотна передавальна функція
.
Амплітудна частотна характеристика
З АЧХ видно, що при малих частотах ( ) відношення амплітуд близьке до коефіцієнта передачі k.
Коливання при частотах ( |
) послаблюються. Чим |
менше Т, тим менша інерційність ланки і тим ширша |
|
смуга пропускання |
ланки |
.
Логарифмічні частотні характеристики будують з виразу
.
Найбільш просто будувати асимптотичну ЛАХ. На стаціонарній сітці проводять вертикальну пряму через точку з частотою, яка називається спряженою
(сполучаючою) і рівна |
. Для частот, менших ніж |
спряжена |
, можна знехтувати другою складовою |
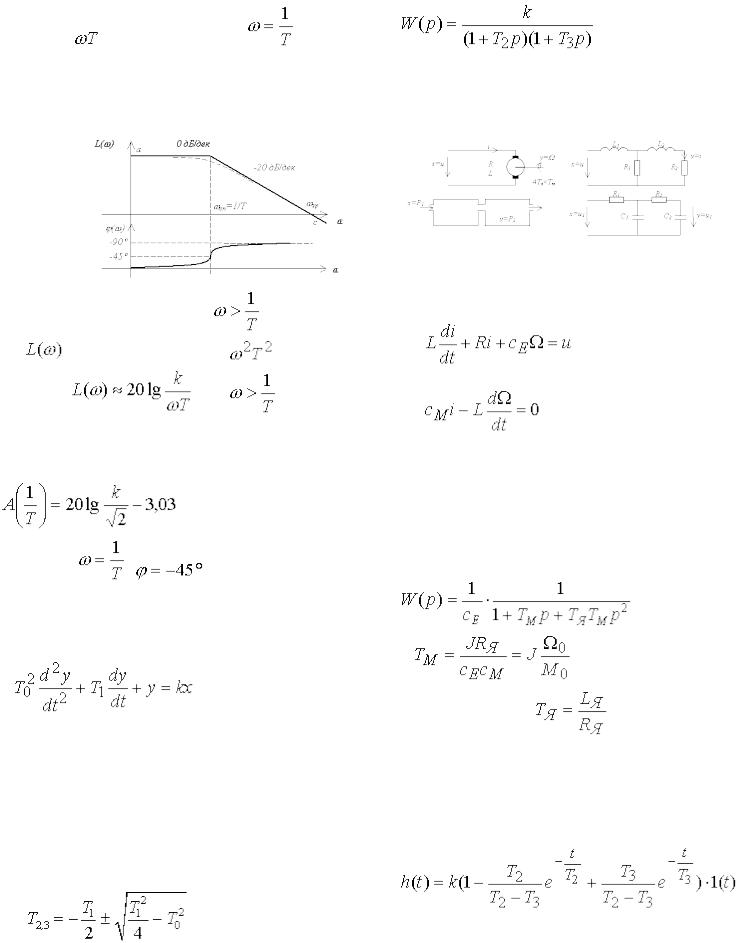
17
під коренем |
. Тоді лівіше від частоти |
вираз |
для 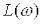 можна замінити наближеним
можна замінити наближеним
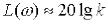 , якому відповідає пряма лінія, паралельна осі частот.
, якому відповідає пряма лінія, паралельна осі частот.
Для частот більших чим спряжена |
, у виразі |
|
для |
нехтуємо 1, в порівнянні із |
. Тоді |
наближено, |
, при |
, якому |
відповідає пряма з від’ємним нахилом 20 дб/дек, яка є другою асимптотою. Ламана а-в-с називається асимптотичною ЛАХ. Дійсна ЛАХ відрізняється від асимптотичної найбільше в т.в. В т.в
дб (тобто різниця =3дб).
ЛФХ в точці |
(так як |
 ).
).
3. Аперіодична ланка другого порядку.
Диференціальне рівняння
При цьому корені характеристичного рівняння 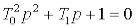 повинні бути дійсними, що
повинні бути дійсними, що
виконується при 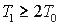 .
.
В операторній формі диф. рівняння має вигляд
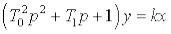 .
.
Ліва частина розкладається на множники
 ,
,
де |
. |
Передавальна функція |
|
.
Аперіодична ланка другого порядку еквівалентна двом послідовно з’єднаним аперіодичним ланкам першого порядку із спільним коефіцієнтом передачі k і сталими
часу Т3 і Т4.
Приклади таких ланок приведені на рис.
Для прикладу розглянемо двигун постійного струму. При відсутності навантаження на валу і враховуючи перехідні процеси в колі якоря, динаміка двигуна описується двома рівняннями:
–рівняння рівноваги е.р.с. в колі якоря:
,
–рівняння рівноваги моментів на валу двигуна:
,
де и – напруга, що прикладена до якоря; 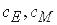 – коефіцієнти е.р.с. і моменту відповідно; J – приведений
– коефіцієнти е.р.с. і моменту відповідно; J – приведений
момент інерції; 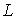 і
і 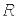 – індуктивність і опір кола якоря.
– індуктивність і опір кола якоря.
Якщо перейдемо до операторної форми і розв’язуємо ці рівняння, то одержимо передавальну функцію як
відношення  до
до 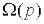
|
, |
де |
– електромеханічна |
постійна часу двигуна; |
– електромагнітна |
постійна часу кола якоря; 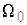 і
і 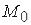 – швидкість холостого ходу і пусковий момент двигуна. Для того, щоб корені знаменника були дійсні, необхідно щоб
– швидкість холостого ходу і пусковий момент двигуна. Для того, щоб корені знаменника були дійсні, необхідно щоб
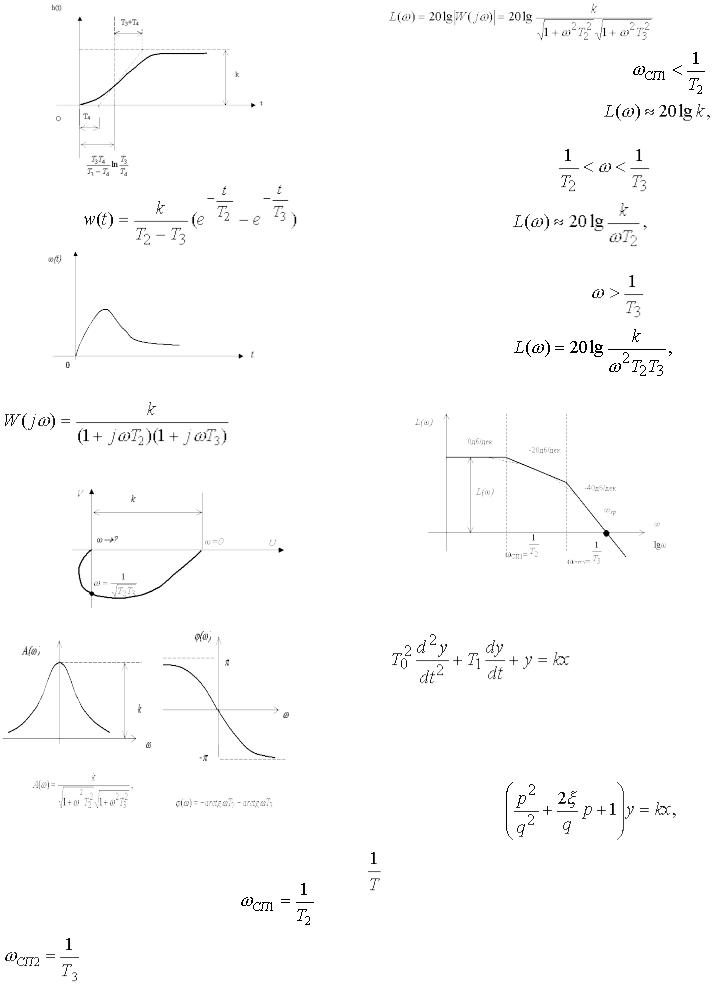
виконувалась нерівність 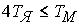 . Перехідна функція
. Перехідна функція
.
18
. |
|
Лівіше першої спряженої частоти ( |
) |
цей вираз замінюють наближеним |
|
якому відповідає пряма з нульовим нахилом |
(перша |
Функція ваги |
. |
Частотна передавальна функція
.
Амплітудна фазова частотна характеристика АФЧХ:
Ампліту
дна
і фазова частотні характеристики.
Будуємо асимптотичну ЛАХ. Проводимо допоміжні
вертикальні лінії через спряжені частоти |
і |
(Т2>Т3). ЛАХ будують по виразу |
|
асимптота ЛАХ). Для частот |
вираз |
(4) |
замінюють приближеним |
|
|
якому відповідає пряма з від’ємним |
нахилом 20 дб/дек |
|
(друга асимптота). Для частот |
вираз |
(4) |
замінюють приближеним |
якому |
|
відповідає пряма з від’ємним нахилом 40 дб/дек (третя асимптота).
4. Коливна ланка.
Диференціальне рівняння те ж саме, що і для аперіодичної ланки 2-го порядку:
Але корені характеристичного рівняння
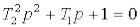 повинні бути комплексними, що буде виконуватися при Т1<2Т2.
повинні бути комплексними, що буде виконуватися при Т1<2Т2.
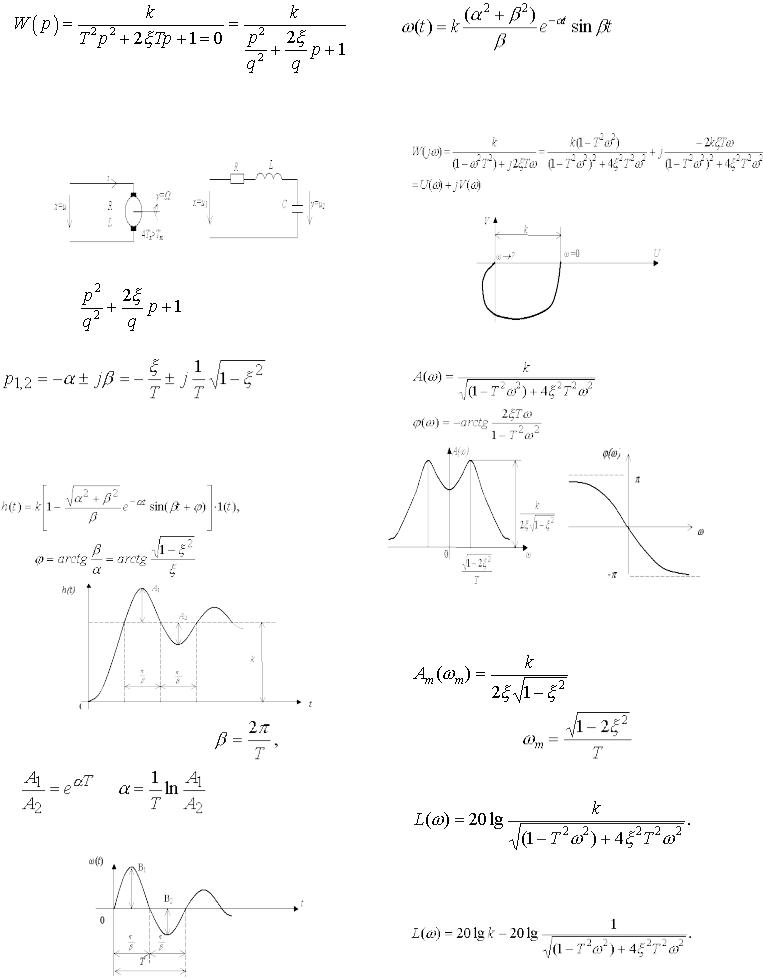
Диференціальне рівняння в операторній формі звичайно представляють в вигляді
(Т2р2+2ξТр+1)у=kx, або |
де q= |
– кутова частота вільних коливань (при відсутності затухання) а ξ – параметр затухання (коефіцієнт демпфування), який лежить в межах 0<ξ<1.
19
Передавальна функція:
.
Прикладами коливних ланок є: коливне RLC – коло, керовані двигуни постійного струму при виконанні умови 4Тя>Тм, пружні механічні передачі, гіроскопічні елементи і ін.
Для розв’язку диференціального рівняння необхідно визначити корені характеристичного рівняння
Т2р2+2ξТр+1= |
=0, |
|
|
|
які |
можна |
записати |
у |
вигляді: |
. При цьому, дійсна частина кореня 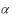 визначає коефіцієнт затухання перехідного процесу, а уявна
визначає коефіцієнт затухання перехідного процесу, а уявна 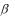 – частоту затухаючих коливань.
– частоту затухаючих коливань.
Часові характеристики коливної ланки:
– перехідна функція і перехідна характеристика
де |
. |
При цьому мають місце рівності |
|
і |
. |
– імпульсна перехідна функція ω(t) (функція ваги) і імпульсна перехідна характеристика:
Частотні характеристики:
–частотна передавальна функція
–амплітудна фазова частотна характеристика
– амплітудна частотна характеристика і фазова частотна характеристика
Амплітудна частотна характеристика може мати резонансний пік. Пік буде існувати при ξ <0,707. Висота піку буде тим більша, чим менший параметр затухання
ξ:
|
. Максимуму АЧХ |
відповідає частота |
. |
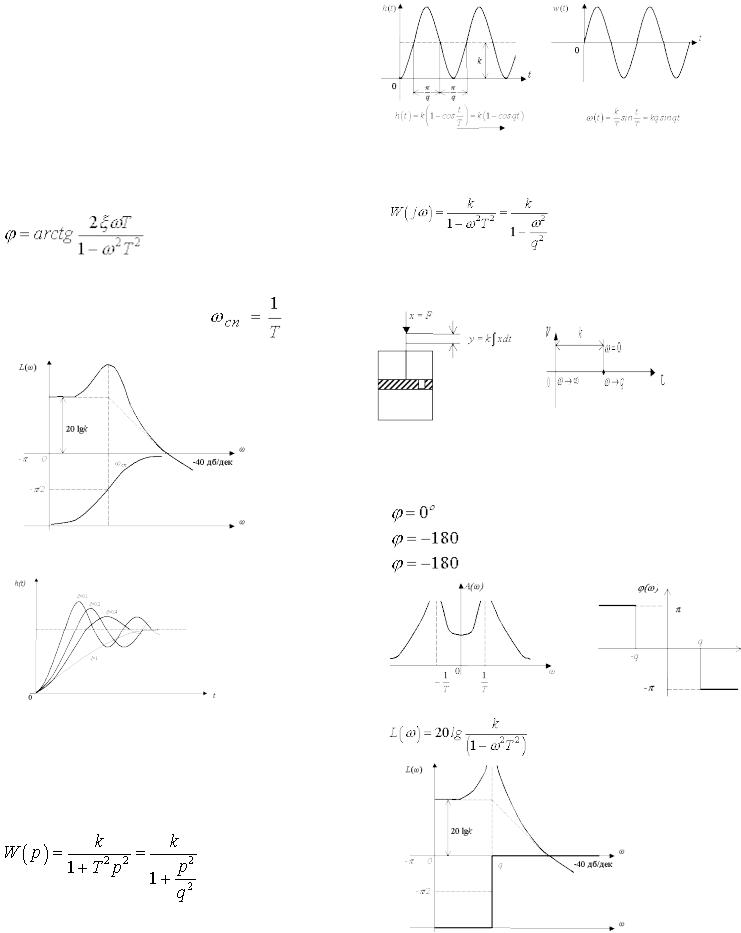
– логарифмічна амплітудна частотна характеристика будується згідно виразу
Але побудова ЛАХ не така проста як для попередніх ланок. Для побудови необхідно використовувати нормовані ЛАХ. Постійний множник під значком lg виділяємо в окрему складову:
20
Побудова першої асимптоти проста – пряма лінія з нахилом 0 дБ/дек. Друга асимптота може бути
побудована в функції відносної частоти 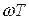 для різних значень параметра затухання ξ в вигляді універсальних (нормованих) кривих.
для різних значень параметра затухання ξ в вигляді універсальних (нормованих) кривих.
Для побудови дійсної ЛАХ необхідно вибрати нормовану ЛАХ, що відповідає даному значенню ξ,
перенести її паралельно самій собі на 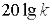 і на осі частоти від відносної частоти перейти до дійсної,
і на осі частоти від відносної частоти перейти до дійсної,
множенням на 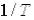 .
.
В функції тієї ж відносної частоти наносяться нормовані ЛФХ, побудовані згідно виразу
.
Побудову ЛАХ консервативної ланки можна отримати також побудовою двох асимптот із нахилом 0 і -40
дБ/дек, які перехрещуються в точці , а потім вводиться поправка згідно нормованих кривих.
Нормовані перехідні характеристики коливної ланки для випадку k=1 приведені на рисунку.
– перехідна характеристика, перехідна функція: – імпульсна характеристика /ф-ція
Частотні характеристики:
.
АФЧХ співпадає з дійсною віссю. При 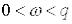 характеристика співпадає з додатною піввіссю, а при
характеристика співпадає з додатною піввіссю, а при
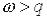 – з від’ємною.
– з від’ємною.
Амплітудна частотна
функція: 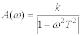 Фазочастотна характеристика:
Фазочастотна характеристика:
при 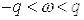 ;
;
при 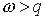 ;
;
при 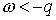 .
.
З
нормованих кривих видно, що зменшення параметра затухання ξ призводить до підвищення коливності перехідного процесу і росту піка амплітудної частотної характеристики.
5. Консервативна ланка
Консервативна ланка є частковим випадком коливної ланки, коли коефіцієнт демпфування рівний нулю (ξ=0).
.
Це є ідеалізований випадок, коли нехтують розсіюванням енергії в ланці. В прикладах, наведених для коливної ланки, консервативна отримується, коли приймається R=0.
Часові характеристики: незатухаючі коливання з кутовою частотою q:
Логарифмічна амплітудна характеристика:
6. Інтегруюча ланка (ідеальна інтегруюча ланка).
Диференціальне рівняння ланки:
