
- •6.3. Синхронна мережа Гопфілда
- •6.4. Неперервна мережа Гопфілда
- •6.5. Асоціативна мережа вsв
- •7. Синергетичний комп’ютер
- •8. Мережа хеммінга
- •9. Динамічні рекурсивні шнм
- •9.1. Структура дрм
- •9.2. Неперервні дрм
- •9.3. Дискретна дрм
- •9.3.2. Частково-рекурсивні мережі
- •9.3.3. Локально-рекурсивні мережі прямого поширення
- •9.4. Навчання дрм
- •9.4.1. Алгоритм зворотного поширення помилки
- •9.4.2. Адаптивний алгоритм навчання
- •10. Мережа векторного квантування
- •10.1. Структура мережі векторного квантування
- •10.2. Неконтрольоване навчання мережі вк
- •10.3. Контрольоване навчання мережі вк
- •10.3.1. Lvq1
- •10.3.2. Lvq2.1
розпізнати
спотворений образ х3=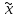 2
=
2
=
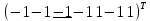 (спотворений
біт підкреслений)
(спотворений
біт підкреслений)
На рис. 6.5 наведена ця мережа й позначені деякі її зв’язки.
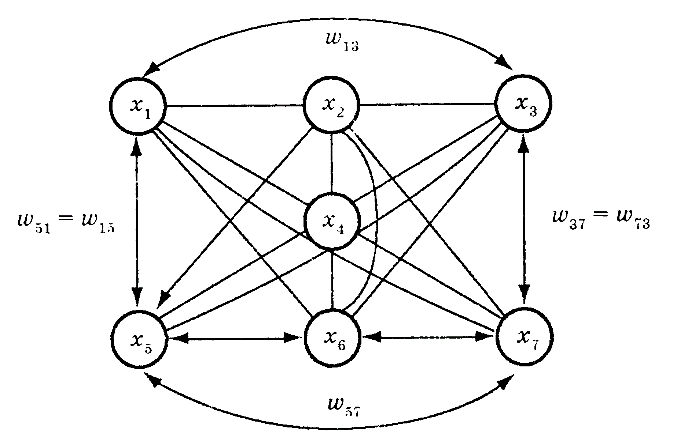
Рис. 6.5. Мережа Гопфілда, що складається з 7 нейронів
Елементи
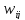 матриці
ваг W розмірності7x7,
що має вигляд
матриці
ваг W розмірності7x7,
що має вигляд
W=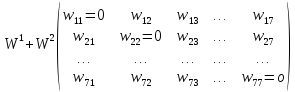 ,
,
де
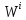 – матриця
ваг для i-го
(i=1,2)
образу, що навчає, визначається за
формулою (6.1)
– матриця
ваг для i-го
(i=1,2)
образу, що навчає, визначається за
формулою (6.1)
w12
= 1 (-1)
+ (-1)
(-1)
+ (-1) (-1)
= 0; w13
= 1
(-1)
= 0; w13
= 1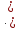 -1)
+ (-1)
-1)
+ (-1) 1
= -2;
1
= -2;
w14
= 1 1
+ (-1)
1
+ (-1) (-1) = 2;w15
= 1
(-1) = 2;w15
= 1 (-1) + (-1)
(-1) + (-1) 1=
-2;
1=
-2;
w16
= 1 1+
(-1)
1+
(-1) (-1) = 2;w17
= 1
(-1) = 2;w17
= 1 1+
(-1)
1+
(-1) 1=
0 и т. д.
1=
0 и т. д.
Після визначення всіх ваг матриця набуває вигляду
W=
Обчислимо енергію кожного образу, беручи до уваги тільки активні нейрони. Для першого образу
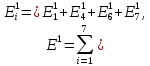
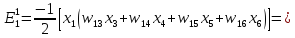
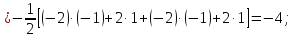
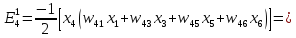
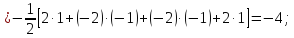
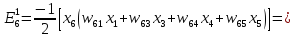
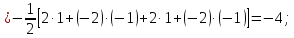
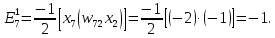
Тоді Е1 = -13. Аналогічно отримуємо для другого образу
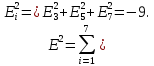
Розпізнавання
образу х3=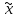 2
починаємо
з визначення його енергії, що після
проведення аналогічних обчислень
дорівнюватиме
2
починаємо
з визначення його енергії, що після
проведення аналогічних обчислень
дорівнюватиме
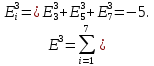
За формулами (6.3) і (6.4) обчислюємо нові стани нейронів і відповідні значення вихідних сигналів, які з урахуванням біполярної активаційної функції дорівнюватимуть
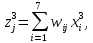
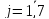
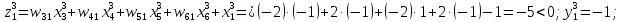
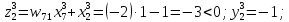
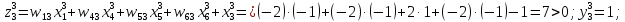
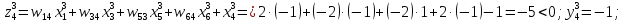
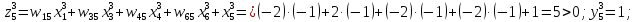
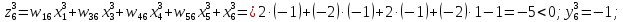
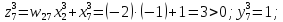
Таким
чином, після подання х3=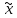 2
мережа
перейде в стійкий
2
мережа
перейде в стійкий
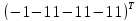 ,
що
відповідає образу
,
що
відповідає образу
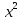 з
енергією, як неважко переконатися, Е
= -9. Отже, мережа правильно розпізнала
(відновила спотворений) образ.
з
енергією, як неважко переконатися, Е
= -9. Отже, мережа правильно розпізнала
(відновила спотворений) образ.
6.3. Синхронна мережа Гопфілда
Як ми вже зазначали, у цій мережі нейрони змінюють свій стан одночасно, прагнучи перейти в деякі стійкі стани. Однак при цьому поняття стійкого стану має дещо інший зміст. Розглянемо це на прикладі.
Приклад
6.4.
Нехай на виходах синхронної мережі
Гопфілда, заданою матрицею ваг
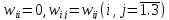 і значеннями порогів
і значеннями порогів
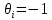 ,
у деякий момент часу к
при подачі на її входи вектора
,
у деякий момент часу к
при подачі на її входи вектора
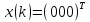 з’являються
одиничні сигнали
з’являються
одиничні сигнали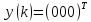 .
Тоді
в наступний (k
+ 1)-й момент часу нейрони перейдуть у
нові стани, визначені відповідно до
(6.3)
.
Тоді
в наступний (k
+ 1)-й момент часу нейрони перейдуть у
нові стани, визначені відповідно до
(6.3)
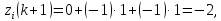
і на їхніх виходах з’являться сигнали
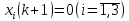 .
.
На
(k
+ 2)-му такті сигнали
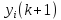 надійдуть
на входи нейронів, переводячи їх у
стани
надійдуть
на входи нейронів, переводячи їх у
стани
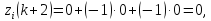
після
чого на їхніх виходах з’являться сигнали
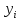 (k
+ 2) = 1 (і
=
(k
+ 2) = 1 (і
=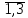 ),
тобто мережа перейшла в початковий
стан. Неважко помітити, що мережа осцилює.
),
тобто мережа перейшла в початковий
стан. Неважко помітити, що мережа осцилює.
Що ж відбувається з енергією мережі? У момент часу k значення енергетичної функції (6.5) дорівнюватиме
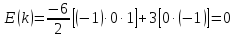
а при переході в новий стан на (к + 1)-му такті
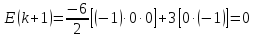
Отже, хоча синхронна мережа осцилює, значення її енергетичної функції не змінюється.
Використання енергетичної інтерпретації дозволяє побачити основну відмінність між синхронним й асинхронним способами активації мережі Гопфілда. Дійсно, випадковий вибір вершини при асинхронній активації призводить до зміни шляху досягнення мережею свого стійкого стану, тобто до зміни послідовності аналізу мережею проміжних образів. Отже, асинхронна активація збільшує деяку невизначеність шляху переходу мережі з початкового в кінцевий стан. При синхронній активації всі вершини оновлюються разом, тому проміжні образи не змінюються. Крім того, мережа осцилює між двома різними станами. Обидва ці способи активації призводять до одного результату, тому звичайно їхній вибір не є принциповим.
6.4. Неперервна мережа Гопфілда
Неперервний варіант мережі Гопфілда є узагальненням дискретної мережі у випадку використання замість порогової функції активації неперервної. Звичайно в якості такої функції використовують синусоїдальну або функцію гіперболічного тангенса, а динаміку мережі описують у неперервному часі. У найбільш загальному вигляді такий опис, запропонований у роботах М. Коєна й С. Ґрос- сберґа [22] ІД ж. Гопфілда [24], може бути поданий у такий спосіб:
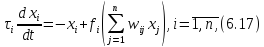
де
 — деяка стала часу;
— деяка стала часу;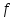 (
( )
— функція активації виду
)
— функція активації виду
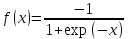 .
.
Система, динаміка якої описується рівнянням (6.17), може або прагнути до деякого стійкого стану, або перебувати в хаотичному русі, або осцилювати. Вибір симетричної матриці вагових коефіцієнтів дозволяє забезпечити рух системи до стійкого стану. При цьому збіжність гарантується теоремою Коєна — Ґроссберґа [22]. Стійкі стани свідчать про те, що система перебуває в рівновазі й справедливо
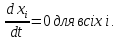
У цьому випадку виходи системи визначаються в такий спосіб:
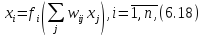
де
 приймає дійсні значення з інтервалу
[0, 1].
приймає дійсні значення з інтервалу
[0, 1].
Динаміка
неперервної мережі Гопфілда може бути
описана за аналогією з (6.17) шляхом заміни
змінних х
на стани нейронів
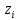
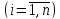

У цьому випадку система диференціальних рівнянь, що описують мережу, набуває вигляду
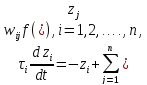
а стійкі стани мережі можуть бути визначені у такий спосіб:
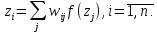
Як й у випадку дискретної мережі, аналіз неперервної мережі Гопфілда може бути проведений за допомогою енергетичної функції. Однак доведення збіжності для неперервної мережі загального вигляду є досить складним. Для аналізу неперервного випадку Гопфілд використав енергетичну функцію такого вигляду:
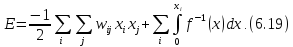
Можна показати, що при переході в стійкий стан, як і в дискретному випадку, енергетична функція мережі зменшується.
