Глава 4. Основы аналитической геометрии.

§1.Уравнение линии на плоскости.

Как известно, любая точка на плоскости определяется двумя координатами в какой- либо системе координат. Системы координат могут быть различными в зависимости от выбора базиса и начала координат.

Пусть на плоскости задана декартова система координат (основные сведения о прямоугольной системе координат считаются известными).

Линия на плоскости рассматривается как множество точек, обладающих некоторым геометрическим свойством. Например, окружность радиуса R– множество всех точек плоскости, удаленных на расстояниеRот некоторой фиксированной точки О (центр окружности).

Положение точки на плоскости определяется заданием пары чисел – ее координат, а положение линии на плоскости определяется с помощью уравнения (т.е. равенства, связывающего координаты точек линии).

Определение. Уравнением линии (или кривой) на плоскостиOxyназывается уравнениеy=f(x), которому удовлетворяют координаты каждой точки этой линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Уравнение линии позволяет заменить изучение геометрических свойств линии исследованием ее уравнения.

Отметим, что уравнение линии может быть выражено параметрическим способом, то есть каждая координата каждой точки выражается через некоторый независимый параметрt:x = (t);

y = (t).

Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.

§2. Уравнение прямой на плоскости. Различные виды уравнений прямой.

Простейшей из линий является прямая, она относится к линиям 1-го порядка, поскольку ее уравнение содержит переменные xи yтолько в первой степени.

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Определение.Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0, (2.1)

причем постоянные А, В не равны нулю одновременно, т.е. А²+ В²0. Это уравнение первого порядка называютобщим уравнением прямой.

Уравнение прямой по точке и вектору нормали.

Определение.В декартовой прямоугольной системе координат векторс компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0 и называетсянормальным векторомэтой прямой.

Пусть имеем следующие начальные условия относительно некоторой прямой: известна точка M₀(x₀,y₀) принадлежащая этой прямой и ее нормальный вектор=(А, В).

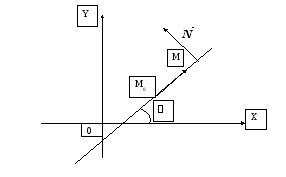
Для произвольной точки М(х, у), принадлежащей прямой, составим вектор . Т.к. вектор - вектор нормали, то он перпендикулярен прямой, а, следовательно, перпендикулярен и вектору. Тогда скалярное произведение

= 0

Таким образом, получаем уравнение плоскости

(2.2)

Из уравнения (2.2) легко получить общее уравнение прямой (2.1), раскрыв скобки и обозначив D = -Ax₀ – By₀.

В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

• C= 0, А0, В0: Ах + Ву = 0 – уравнение прямой, проходящей через начало координат;

• А = 0, В 0, С0:By+C= 0- уравнение прямой, параллельной оси Ох;

• В = 0, А 0, С0:Ax+C= 0 – уравнение прямой , параллельной оси Оу;

• В = С = 0, А 0: Ах = 0 (х = 0) – уравнение координатной оси Оу;

• А = С = 0, В 0:By= 0 (y= 0) – уравнение координатной оси Ох.

Пример.Найти уравнение прямой, проходящей через точку М(1, 2) перпендикулярно вектору(3, -1).

Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С, подставим в полученное выражение координаты заданной точкиM:

3 – 2 + C= 0, следовательно С = -1.

Итого, искомое уравнение: 3х – у – 1 = 0.