2. Однородные линейные дифференциальные уравнения с частными производными и свойства их решений. Если в уравнении (7) правая часть равна нулю, то уравнение на­зывается однородным. Оно имеет вид

(8)

Вообще в теории дифференциальных уравнений уравне­ние называется однородным, если функция, тождественно равная нулю () , является его решением. Решения ли­нейных однородных уравнений вида (8) обладают следующим свойством:

Если каждая из функций является решением уравнения (8), то и их линейная комбинация

(9)

где — произвольные постоянные, также является решением этого уравнения.

Для доказательства достаточно заметить, что если и есть линейная комбинация частных решений:

(для краткости аргументы функций не пишутся), то любая производная функции и будет такой же линейной комбина­цией соответствующих производных функций

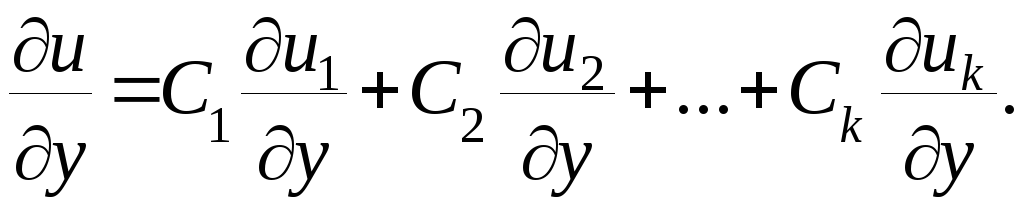
Разумеется, так же будут выглядеть и производные вто­рого порядка. Если подставить выражения для производных функций в левую часть уравнения (8) и перегруппировать слагаемые, то получим

Поскольку по условию функции являются ре­шениями уравнения (8), то каждая из скобок обратится и нуль, а вместе с ними и вся левая часть уравнения; это и означает, что функция и является его решением.

Точно такое же свойство, как известно, имеет место и для обыкновенных линейных дифференциальных уравнений. Однако надо иметь в виду, что обыкновенное линейное диф­ференциальное уравнение n-го порядка имеет в точности n линейно независимых частных решений, линейная комбинация которых и дает общее решение.

Уравнение же в частных производных может иметь, как мы убедимся в дальнейшем, бесконечное множество ли­нейно независимых частных решений, т. е. такое мно­жество решений, любое конечное число которых является функциями линейно независимыми. (Система функций называется линейно независимой, если ни одна из этих функций не является линейной комбинацией опальных.) В соответствии с этим нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с р яд а м и, членами которых служат произве­дения произвольных постоянных на частные решения:

(10)

Мы дадим здесь необходимые определения и укажем некото­рые свойства рядов, членами которых являются функции не­скольких переменных. Этими свойствами мы будем пользо­ваться и в дальнейшем.

Будем считать, что члены ряда — функции двух перемен­ных; все определения легко переносятся на случай функций трех переменных.

Рассмотрим функциональный ряд

(11)

Этот ряд называется сходящимся в точке , если числовой ряд сходится. Совокупность всех точек, в которых ряд сходится, называется областью сходимости ряда. Все члены ряда считаются непрерывными и дифференцируемыми функциями переменных х и у во всей области сходимости ряда.

Мы будем в дальнейшем рассматривать только такие ряды, суммы которых есть непрерывные функции от х и у,

(2)

Кроме того, будем предполагать, что все встречающиеся ряды можно дважды почленно дифференцировать, т. е. что

(13)

и т.д.

Очень часто нам придется интегрировать ряд (12) либо по некоторой области D, либо по одной из переменных. По­следнее означает, что мы полагаем, напримери ин­тегрируем по х в некоторых пределах от до . Возмож­ность почленного интегрирования ряда заключается в том, что

(14)

(Разумеется, предполагается, что рассматриваемые значе­ния х и принадлежат области сходимости ряда.)

Обозначим сумму ряда (10) через и будем считать, что выполняются все введенные предположения. Тогда

Отсюда ясно, что функция —сумма ряда (10), так же как и члены ряда, является решением уравнения (8).

Можно указать сравнительно простые признаки, при соблюде­нии которых все высказанные предположения о рядах будут спра­ведливы. Введем для этого следующее определение.

Функциональный ряд

называется правильно сходящимся в области D, принадлежа­щей области сходимости ряда, если все члены его по абсолют­ной величине не превосходят соответствующих членов некото­рого сходящегося знакоположительного числового ряда, т. е.

причем неравенство соблюдается во всех точках области D, а — член сходящегося числового ряда.

Для правильно сходящихся рядов имеют место следующие тео­ремы, которые мы приводим без доказательства.

1. Сумма правильно сходящегося ряда из непрерывных функ­ций есть функция непрерывная.

2. Правильно сходящийся ряд можно почленно интегриро­вать.

3. Если ряды, составленные из производных сходящегося ряда, сходятся правильно, то ряд можно почленно дифферен­цировать.

Определение правильно сходящегося ряда без всяких измене­ний переносится как на функции одной переменной, так и на функ­ции трех и большего числа переменных.

Напомним, что все три сформулированные свойства имели место для степенных рядов в интервале их сходимости. Нетрудно показать, что степенной ряд является правильно сходя­щимся в любом интервале, целиком заключенном в интервале схо­димости ряда (см. [1], п. 190). { Для читателей, знакомых с определением равномерной схо­димости ряда, отметим, что если ряд сходится правильно, то он сходится и равномерно; однако не всякий равномерно сходящийся ряд сходится правильно.}

В дальнейшем нам встретятся и такие случаи, когда функ­ция при всех значениях параметра , заключен­ных в некотором интервале , является решением урав­нения (8). Тогда говорят, что частные решения зависят от непрерывно изменяющегося параметра. Обычно ин­тервал изменения параметра составляет или всю числовую ось, или положительную полуось.

Мы будем в дальнейшем функцию записывать в виде . Этой формой записи подчеркивается анало­гия между случаями, когда решения зависят от параметра, принимающего только целые значения (), и когда решения зависят от параметра, принимающего любые значения ().

Покажем, что если мы умножим функцию на произвольную функцию С() и проинтегрируем в пределах изменения параметра :

(15)

то вновь получим решение уравнения (8). Ясно, что инте­грал (15) есть некоторая функция переменных х и у.

Предварительно познакомимся с некоторыми свойствами интегралов типа (15). Пусть дан интеграл

(16)

где и — конечные пределы. Имеет место следующая теорема, которую мы приводим без доказательства.

Если подынтегральная функция , а также ее частные производные по х и по у непрерывна при всех рассматриваемых значениях аргументов х, у и то и функция F(x, у) непрерывна вместе со своими частными производными, причем

(17)

и т. д.

В случае, когда хотя бы один из пределов интегриро­вания обращается в бесконечность, интеграл (16) ста­новится несобственным и указанные свойства функции F(x, y) соблюдаются лишь при некоторых дополнительных условиях, о которых мы скажем ниже.

Возвращаясь к интегралу (15), обозначим его через U(x, у) и предположим, что для него справедливы фор­мулы (17). При этом пределы интегрирования и могут быть как конечными, так и бесконечными. Тогда

и т. д.

Подставляя выражения для функции U(x, у) и ее про­изводных в уравнение (8) и заменяя сумму интегралов ин­тегралом от суммы функций, получим в левой части

Так как по предположению выражение в квадратных скобках при любом равно нулю (ведь функция при любом является решением уравнения (8)), то и весь интеграл равен нулю. Следовательно, функция U (x, у) дей­ствительно является решением уравнения.

Сформулируем простой признак, аналогичный соответствую­щему признаку для рядов, при соблюдении которого выполняются все приведенные свойства для несобственных интегралов вида где один или оба предела интегрирова­ния обращаются в бесконечность.

Если можно указать такую положительную функцию , что для всех рассматриваемых значений х, у и соблюдается неравенство и несобственный интеграл от функции сходится, то функция F(x, у) непрерывна. Такую сходимость несобственного интеграла от функции будем называть правильной.

Если аналогичное свойство имеет место и для интегралов от частных производных функции , то функция F (х, у) дифференцируема и ее производные находятся по формулам (17). Например, если — и интеграл от сходится, то

3. Оператор Лапласа в полярных, цилиндрических и сферических координатах. { Этот пункт следует прочесть или перед изучением задач, в которых встретится необходимость преобразования оператора Лапласа (п. 32, п. 49—50), или перед чтением гл. III } В этом пункте мы рассмо­трим вспомогательный вопрос о выражении оператора Лап­ласа о различных системах координат; эти выражения пона­добятся нам в дальнейшем. Напомним, что трехмерным оператором Лапласа называется выражение

(18)

где — функция трех переменных. Если функция и зависит только от двух переменных, то оператор Лапласа

(19)

называется двумерным.

Начнем с двумерного оператора Лапласа и произведем замену декартовых координат х и у полярными r и по формулам

(20)

Если в функцию подставить вместо x и у их выражения, то получится функция перемен­ных r и . Выразив вторые производные от функции u по х и по у через производные по r и и подставив затем найденные выражения в формулу (19), мы и получим опера­тор Лапласа в полярных координатах.

По правилу дифференцирования сложной функции

(21)

Для отыскания частных производных r и по х и у выразим из формул (20) r и . Находим, что отсюда

и (22)

Поскольку , то

и

Заменяя х и у по формулам (20), получим

и (23)

Подставив (22) и (23) в равенства (21), окончательно найдем выражения частных производных и через пере­менные r и и производные по этим переменным:

(24)

Перейдем к отысканию вторых производных. Применим к производной опять правило дифференцирования слож­ной функции

Из равенств (24) ^д{дї) д*и

Умножим теперь первое равенство на , а второе на и сложим. Приводя подобные члены, по­лучим

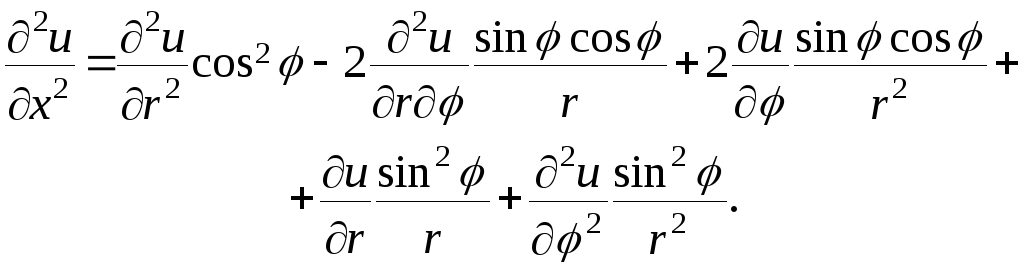(25)

Совершенно аналогично, воспользовавшись соотношением

найдем, что

(26)

Складывая (25) и (26), окончательно получим выражение оператора Лапласа в полярных координатах:

(27)

Последнее выражение очень часто бывает удобно запи­сать в следующем виде:

(28)

Тождественность правых частей формул (28) и (27) легко проверяется дифференцированием.

Перейдем к трехмерному случаю и начнем с цилин­дрических координат. Цилиндрические координаты r , и z связаны с декартовыми соотношениями

Функция преобразуется в функцию . Здесь третья переменная z остается неизменной, и в выражении (27) двумерного оператора Лапласа в поляр­ных координатах добавляется только вторая производная по z:

(29)

Для сферических координат r , и имеем формулы:

в которых — расстояние точки (х, у, z) от начала координат, — угол между радиусом-вектором точки и осью Oz, а — угол между проекцией радиуса- вектора на плоскость Оху и осью Ох. Здесь непосредствен­ное преобразование производных функции очень громоздко, и мы его проводить не будем, ограничившись тем, что выпишем окончательное выражение оператора Лапласа в сферических координатах:

Эту формулу часто записывают в виде

(31)

Предоставляем читателю проверить тождественность обеих формул.