
- •Лекция 16. Математические модели средств измерений с распределенными параметрами
- •Классификация линейных дифференциальных уравнений с частными производными второю порядка.
- •69. Корректность постановки задач математической физики.
- •Практическое заеятие § 3. Метод Фурье
- •10. Метод Фурье. Мы рассмотрим в этом параграфе задачу о свободных колебаниях струны, закрепленной на обоих концах. Как указано в § 1, задача сводится к решению однородного уравнения струны
- •Дополнительный материал
- •Введение
- •2. Однородные линейные дифференциальные уравнения с частными производными и свойства их решений. Если в уравнении (7) правая часть равна нулю, то уравнение называется однородным. Оно имеет вид
Классификация линейных дифференциальных уравнений с частными производными второю порядка.
Общий вид линейного дифференциального уравнения второго порядка при условии, что неизвестная функция u зависит от двух переменных x и y, таков:
 (1)
(1)
Предполагаем, что все коэффициенты уравнения постоянны {Приводимая ниже классификация линейных уравнений переносится и на уравнения с переменными коэффициентами, которые здесь не рассматриваются}.
Большинство дифференциальных уравнений второго порядка математической физики представляют частные случаи общего уравнения (1).
Так, если для единообразия обозначений вместо переменной t (времени) писать переменную y, то уравнение свободных колебаний струны (§ 1) примет вид
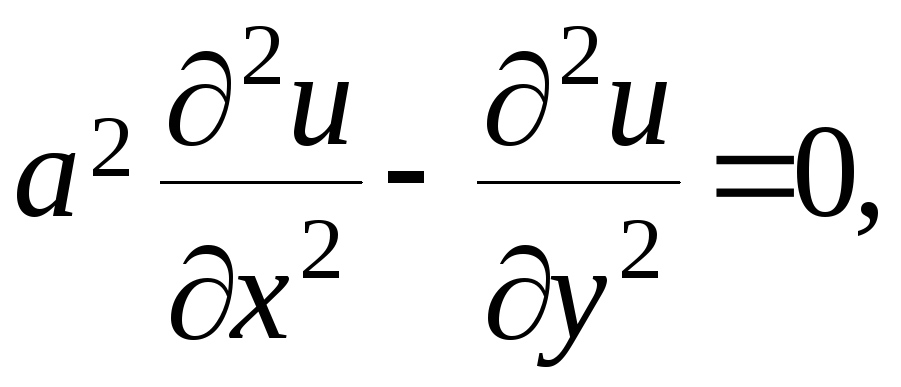 (2)
(2)
a уравнение линейной задачи теплопроводности (§ 12)
 (3)
(3)
Наконец, уравнение Лапласа (§18) в двумерном случае имеет вид
 (4)
(4)
В уравнении (4) обе вторые частные производные входят в левую часть с одинаковыми знаками, в уравнении (2) — с противоположными знаками, а в уравнении (3)—вторая производная по одной из переменных вовсе не входит.
Л. Эйлер доказал, что любое дифференциальное уравнение вида (1) с помощью замены независимых переменных x и y может быть приведено к одному из следующих трех видов.
-
Если
 то
после введения новых независимых
переменных
то
после введения новых независимых
переменных
 и
и

{мы ограничимся только принципиальной стороной вопроса и не указывая формул, по которым фактически производится замена переменной } уравнение (1) примет вид
 (5)
(5)
В этом случае уравнение называется эллиптическим. Наиболее простым эллиптическим уравнением является уравнение Лапласа (4).
-
Если
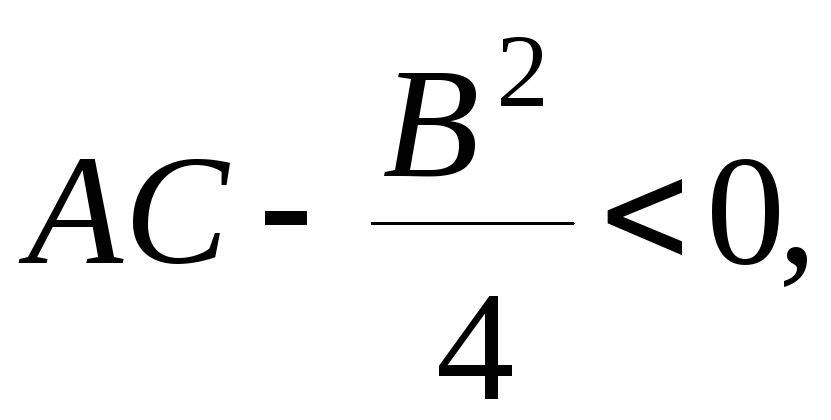 то уравнению (1) можно придать вид
то уравнению (1) можно придать вид
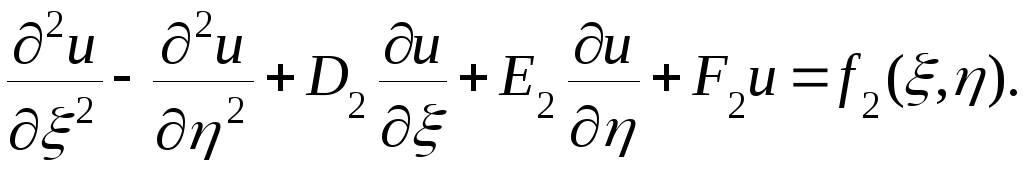 (6)
(6)
Такое уравнение называется гиперболическим; простейшим примером его является одномерное уравнение свободных колебаний (2).
-
Если
 то
уравнение (1) приводится
то
уравнение (1) приводится
к следующему:
 (7)
(7)
и называется параболическим. Примером его служит уравнение линейный теплопроводности (3).
Наименования
уравнений объясняются тем, что при
исследовании общего уравнения кривых
второго порядка
![]() оказывается,
что в случае
оказывается,
что в случае
 кривая представляет эллипс, в случае
кривая представляет эллипс, в случае
 —
гиперболу и в случае
—
гиперболу и в случае
 - параболу.
- параболу.
{Поскольку бывают еще случаи вырождения кривых второго порядка, то чаще говорят, что в первом случае кривая эллиптического типа, во втором — гиперболического и в третьем— параболического (см., например, книгу Н. В. Ефимова «Квадратичные формы и матрицы», Физматгиз, М., 1967)}
Уравнения
(5), (6) и (7) можно еще более упростить
введением новой неизвестной функции.
Именно, вводя функцию
![]() по
формуле
по
формуле
![]() (8)
(8)
мы
можем всегда подобрать числа
![]() и
и
![]() так, что в эллиптическом и гиперболическом
уравнениях исчезнут члены с производными
первого порядка, а в параболическом —
член с первой производной по одной из
независимых переменных (в уравнении
(7) по
так, что в эллиптическом и гиперболическом
уравнениях исчезнут члены с производными
первого порядка, а в параболическом —
член с первой производной по одной из
независимых переменных (в уравнении
(7) по
![]() )
и член с самой функцией.
)
и член с самой функцией.
Введение вспомогательной функции по формуле (8) уже встречалось нам в п. 21 при изучении телеграфного уравнения для линии без искажений (см. формулу (7.13)).
Окончательно любое уравнение вида (1) может быть, с учетом сделанных замечаний, приведено к одному из следующих канонических типов:
 (эллиптический
тип),
(эллиптический
тип),
 (гиперболический
тип),
(гиперболический
тип),
 (параболический
тип)
(параболический
тип)
(с—постоянное число, g — функция переменных х и у).
