69. Корректность постановки задач математической физики.

Уравнения гиперболического и параболического типов возникают чаще всего при изучении процессов, про­текающих во времени (это были колебаний, распространения электрических волн, распростра­нения тепла, диффузии). В одномерном случае всегда уча­ствовала одна координата х и время t.

Поэтому канонические уравнения этих типов обычно за­писываются так:

(гиперболический тип),

(параболический тип).

Для задач, приводящих к таким уравнениям, дополни­тельные условия разделяются на начальные и краевые.

Начальные условия, как мы видели, состоят в задании при t = 0 значений искомой функции u и ее про­изводной (в гиперболическом случае) или только значений самой функции (в параболическом случае).

Краевые условия для этих задач заключаются в том, что указываются значения неизвестной функции u(x, t) на концах интервала изменения координаты (в задаче о коле­баниях струны эго концы струны {в задаче о колебаниях мембраны задаются значения неиз­вестной функции на контуре мембраны}, в задаче о распростра­нении электрических колебаний это концы линии, в задаче о линейной теплопроводности это концы стержня и т. д.) .

Если процесс протекает в бесконечном интервале изменения координаты х (бесконечная струна, бесконечный стержень), то краевые условия отпадают и получается за­дача только с начальными условиями, или, как ее часто называют, задача Коши.

Если ставится задача для конечного интервала, то должны быть заданы и начальные и краевые условия. Тогда говорят о смешанной задаче.

Уравнения эллиптического типа возникают обычно при исследовании стационарных процессов. Время t в эти уравнения не входит, и обе независимые переменные являются координатами точки. Такими оказываются уравнения стацио­нарного температурного поля, электростатического поля и уравнения многих других физических задач.

Для задач такого типа ставятся только краевые усло­вия, т. е. указывается поведение неизвестной функции на контуре области. Это может быть задача Дирихле, когда заданы значения самой функции; задача Неймана, когда заданы значения нормальной производной искомой функции, и, наконец, задача, когда на контуре задана линейная комбинация функции и ее нормальной производной.

В основных задачах математической физики, именно физические соображения подсказывают, какие дополнительные условия следует поста­вить в той или иной задаче, чтобы получить единственное ее решение, отвечающее характеру изучаемого про­цесса.

Практическое заеятие § 3. Метод Фурье

10. Метод Фурье. Мы рассмотрим в этом параграфе за­дачу о свободных колебаниях струны, закрепленной на обоих концах. Как указано в § 1, задача сводится к решению одно­родного уравнения струны

(3,1)

при начальных условиях

(3,2)

и краевых условиях

(3.3)

Метод Фурье (или, как его еще называют, метод раз­деления переменных) принадлежит к -числу важнейших ме­тодов решения уравнений математической физики. Мы с ним будем в дальнейшем неоднократно встречаться.

Первая часть метода Фурье состоит в том, что мы отыскиваем частные решения уравнения (3.1), удовлетворяющие краевым условиям (3.3), вида

(3.4)

Каждое из искомых частных решений, таким образом, представляется в виде произведения двух функций, одна из которых зависит только от х, а другая — только от t.

Дифференцируя дважды выражение (3.4) по х и по t, получим

(Для сокращения записи мы не пишем аргументов функций Х(х) и T(t).)

Подставляя выражения для производных в уравнение (3.1), получим

или, деля обе части равенства на произведение ,

(3.5)

Чтобы функция была решением уравнения (3.1), равенство (3.5) должно соблюдаться при всех зна­чениях х и t. Левая часть этого равенства зависит только от переменной t и не может изменяться при изменении х. Поэтому, если зафиксировать t и менять х, левая часть, а следовательно и правая, будет сохранять постоянное зна­чение. Рассуждая аналогично, установим, что правая часть, а следовательно и левая, не может изменяться и при изме­нении t. Это будет справедливо только в том случае, когда обе части равенства (3.5) вообще не зависят ни от х, ни от t, т.е. когда оба отношения и являются величинами постоянными:

(3.6)

Отсюда следует, что функции T и X должны удовле­творять дифференциальным уравнениям

и (3.7)

Поскольку мы ищем частные решения, удовлетворяющие краевым условиям (3.3), то при любом значении t должны соблюдаться равенства

.

Если бы обращался в нуль второй множитель, то реше­ние равнялось бы пулю при всех значениях х и t. Поэтому, чтобы отыскать решения, не тождественно равные нулю (а только такие нас и интересуют), мы должны счи­тать, что

и

В результате для отыскания функции Х(х) мы пришли к следующей задаче { Эта задача является частным случаем общей задачи Штурма—Лиувилля, заключающейся в отыскании решений линей­ного дифференциального уравнения второго порядка вида , удовлетворяющих некоторым краевым усло­виям, т. е. условиям, налагаемым на искомую функцию или ее про­изводную в точках х = а и х=b (концах интервала).}: найти решения линейного дифферен­циального уравнения второго порядка

(3.8)

при условиях

(3.9)

Разумеется, эта задача при любом с имеет решение, то­ждественно равное нулю: . Оказывается, однако, что при некоторых значениях постоянной с эта задача имеет и другие решения.

Заметим, что в этом состоит существенное отличие реше­ния рассматриваемой задачи от решения обыкновенных диф­ференциальных уравнений с начальными условиями, когда для определения частного решения задаются значения функции и ее производной в некоторой начальной точке. Как известно (см. введение), последняя задача имеет единственное решение.

Полагая 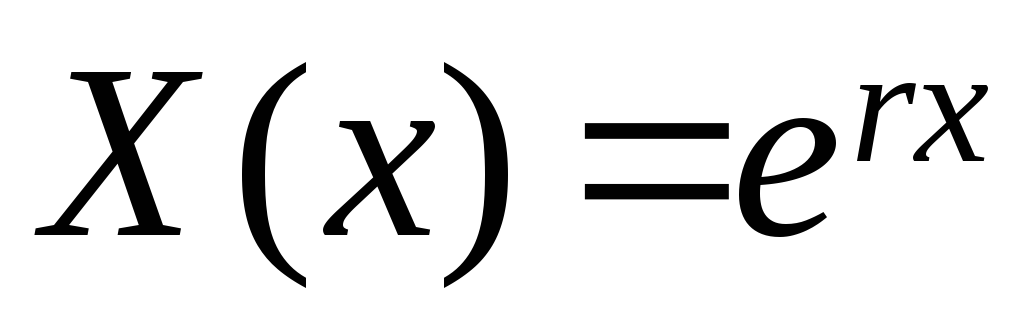, составим для уравнения (3.8) харак­теристическое уравнение

и рассмотрим различные случаи.

1. Пусть . Тогда корни характеристического уравнения действительны, , и общее решение урав­нения имеет вид

Чтобы соблюдались условия (3.9), мы должны положить

Так как определитель этой однородной системы 1 1

не равен нулю, то система имеет единственное решение

Таким образом, в этом случае решений, отличных от тожде­ственного нуля, не существует.

2. Пусть с = 0. Тогда оба корня характеристического уравнения равны нулю и

Подставляя в условия (3.9), получим

т. е. опять-таки .

3. Пусть, наконец, . Корни характеристиче­ского уравнения чисто мнимые, 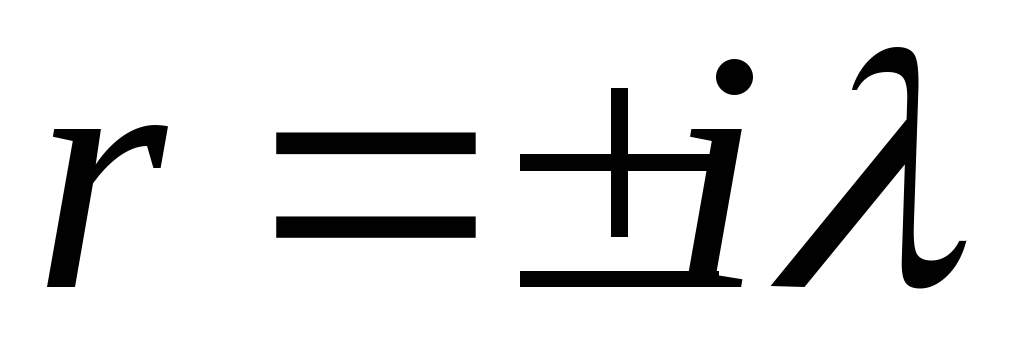, и решение будет содержать тригонометрические функции

При х = 0 должно быть

,

а при х=l

Последнее равенство возможно, когда , именно оно будет удовлетворяться при

т. е. при

(k не равно нулю, так как по условию ).

Итак, если т. е. то сущест­вуют решения уравнения (3.8), не равные тождественно нулю.

Решение, отвечающее некоторому фиксированному к, обозначим через . Оно имеет вид

(3.10)

где — произвольная постоянная. Мы вправе в дальнейшем придавать k только положительные значения: k =1, 2,… поскольку при отрицательных k будут получаться решения того же вида (ведь — произвольные постоянные, которые могут иметь любые знаки).

Как мы видим, каждому значению соответствует бесчисленное множество решений (3.10), отличающихся друг от друга постоянным множителем.

Величины называют собственными числами, а функции собственными функциями дифферен­циального уравнения (3.8) с краевыми условиями (3.9).

Напомним читателю, что система функций называется ортогональной в интервале [а, b], если интеграл от произведения любых двух различных функций системы равен нулю: если (см. [1], п. 205). Легко установить, что найденные собствен­ные функции ортогональны на интервале [0, l]. Действи­тельно, при

Теперь обратимся к отысканию функций T(t). Каждому собственному числу будет соответствовать своя функ­ция , определяемая вторым из уравнений (3.7) (напоми­наем, ):

Его общее решение имеет вид

(3.11)

где и — произвольные постоянные.

Подставляя выражения (3.10) и (3.11) в формулу (3.4), найдем частные решения уравнения (3.1), удовлетворяющие краевым условиям (3.3). При этом каждому значению k=1, 2, ... будет отвечать решение

.

Внося множитель в скобку и вводя обозначения и 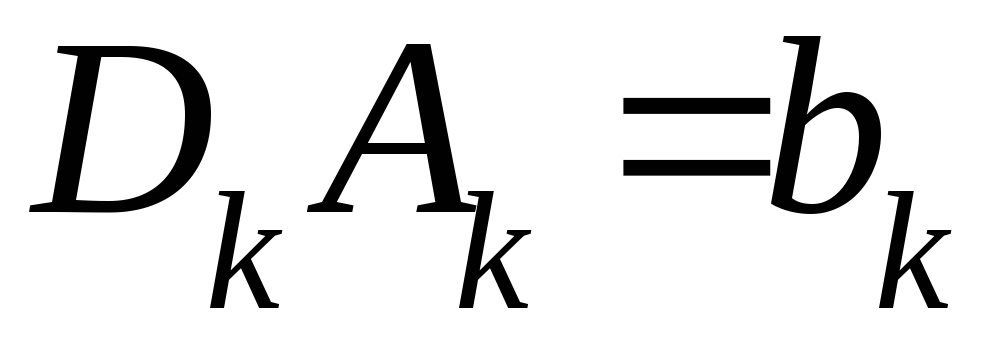, запишем в виде

. (3.12)

Решения называются собственными функциями задачи; соответствующие им колебания струны называются собственными колебаниями.

Физический смысл решений (3.12) мы рассмотрим не­сколько позже, а сейчас перейдем ко второй части метода Фурье и при помощи собственных функций построим реше­ние, удовлетворяющее начальным условиям (3.2). Для этого возьмем сумму решений (3.12), которая в силу линейности и однородности уравнения (3.1) также будет являться его решением:

, (3.13)

Поскольку мы составили бесконечный ряд, то, разумеется, нужно, чтобы он был сходящимся. Мы предположим также, что его можно дважды почленно дифференцировать (см. введение). Ясно, что функция удовлетворяет краевым условиям (3.3), так как им удовлетворяет каждая из функций .

Будем теперь подбирать произвольные постоянные и так, чтобы функция (3.13) удовлетворяла начальным условиям. Подставляя значение t=0, получим

. (3.14)

Дифференцируя ряд (3.13) по t;

,

и подставляя t=0, удовлетворим второму начальному усло­вию:

(3.15)

Формулы (3.14) и (3.15) показывают, что величины и являются коэффициентами разложения функций f(х) и F(x) в ряд Фурье по синусам в интервале (см. [1], п. 201). Вспоминая формулы для коэффициентов этого разложения, найдем :

(3.16)

Так как , то

.

Подставляя выражения для коэффициентов и в ряд (3.13), мы окончательно найдем решение поставленной за­дачи.

Мы не останавливаемся на условиях, которые надо наложить на функции f(x) и F(x), чтобы было оправдано сделан­ное допущение о возможности почленного дифференцирования ряда (3.13). Обычно в физических задачах эти условия соблю­даются.

Формула (3.13) показывает, что в моменты времени струна возвращается в свое первона­чальное состояние; это означает, что колебания струны незатухающие и периодически повторяющиеся, с периодом . Так происходит потому, что мы пренебрегли си­лами трения. При учете их получились бы затухающие коле­бания, аналогично тому как это имеет место в случае обык­новенных гармонических колебаний точки. Решение задачи в этом случае приведено в п. 14.