Metodichka_chast_1

Отримаємо:

2x 2

3y 2

216 або

1

1

x 2

y 2

1

1

1

– канонічне рівняння

еліпса

в

новій системі координат

x1O1 y1 .

108

72

Причому,

a

108

10 , b

72 8 .

3) x 2 6 y 12 x 42 0 .

Розв’язання:

Виділяємо повний квадрат: x 2

2x 6 36 36 6 y 42 0 ,

у

у1

x 6 2 6 y 6 0 ,

x 6 2 6 y 1 – рівняння визначає

О

6

параболу.

Перейшовши до нової системи

–1

х

координат x1O1 y1

:

О1

х1

x

x 6

1

y 1

із початком координат в

y1

точці O 6, 1 , отримаємо: x 2

6 y .

1

1

4) x 2 5 6y y 2 .

Розв’язання:

у

x 2 4 5 6 y y 2 ;

x 2

20 24 y 4 y 2 ;

4 y 2 24 y x 2 20 ;

О

x 2 4 y 2 6 y 20 .

–1

Виділяємо повний квадрат:

х

–4

О1(0;–3)

x 2

4 y 3 2

9

20 ;

х1

x 2

4 y 3 2

16

. Задане рівняння

визначає ліву половину зміщеного

еліпса.

Для побудови

перейдемо до

нової системи координат x1O1 y1 :

x

x

,

а початок координат визначається точкою O1 0, 3 .

1

y

y1

3

Отримаємо:

x

2 4 y 2 16 .

1

1

x 2

y 2

1 – канонічне рівняння еліпса, причому а=4, b=2.

1

1

16

4

Поворот осей координат

y

Поворот осей координат на кут здійснюється за

k >0

формулами:

y1

x1

x x1 cos y1 sin

– перехід від старих до нових

y x1

sin y1 cos

координат.

O

x

Доведемо, що xy k є гіпербола, розташована у І і ІІІ

чверті

при

k

– додатному і в ІІ

і IV

чверті при k -

від’ємному.

Розглянемо рівняння xy k 2 .

Зробимо

поворот

осей

координат

y

tg 2 1 0 ,

k<0

tg 1 .

y1

Прийнявши,

що

,

отримаємо

x1

4

O

x x1 2

2

2

y1

2 2 2

k 2 ,

2

2

2

2

x 2 y 2 2k 2

,

1

1

x 2

y 2

1

– рівняння гіпербол.

2k 2

2k 2

1

1

Приклади

Побудувати криві:

1)

y

3x 2

.

2 2x

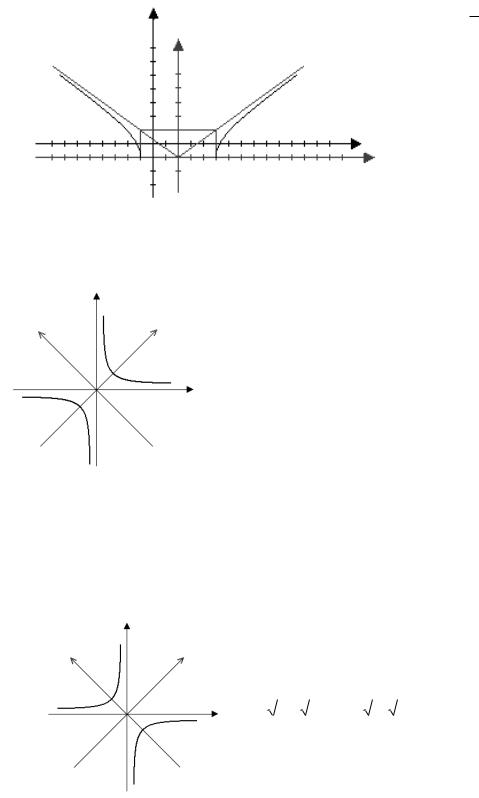
42

у у1

Поділимо 3x 2

на 2 2x :

3x 2

2 2x

3x 3

3/2

1

x

x 1

координат

x1O1 y1

–

1

3

із

y

y1

2

3

1

1

початком в точці

O

1,

, отримаємо рівняння гіперболи:

y

1

, або

x y

.

1

2

2x1

1 1

2

2) y

2 x

.

2x 4

Розв’язання:

у

Зробивши наступні перетворення заданої

у1

функції:

y

1

4

,

2

2x

4

y

1

4

,

О

х

2 2x 4

1

2

y

, перейдемо до нової системи

О1

х1

2

x 2

x

x 2

1

1 , а

координат x1O1 y1 , де

y

y1

2

2,

1

O1

.

2

Отримаємо рівняння гіперболи:

x1 y1 2 .

Число z x iy називається комплексним числом , де x, y – дійсні числа, i

– уявна

одиниця ( i 1 ).

y

x Re z

–

дійсна

частина

комплексного

числа;

y Im z

–

уявна

частина

комплексного

y

P(x,y)

числа.

Два комплексні числа називаються рівними,

r

z

якщо у них рівні і дійсні, і уявні частини.

Число z x iy

називається

спряженим

до

числа z x iy .

O

x

x

Комплексні

числа

зображаються

у

комплексній площині xOy точками або радіус

векторами з координатами Р(x,y). Вісь Оx – дійсна, Oy – уявна.

Якщо z x iy ,

то можна

записати, що x r cos ,

y r sin ,

де r

довжина

Відомо, що i 2 1,

i 3 i,

i 4 1.

z n r n (cos n i sin n ) .

n

n

(cos 2 k

i sin

2 k ) , де k 0;1; 2; ; n 1 .

4.

z

r

n

n

3)

i 3

(i 3)(2 3i)

2i 6

3i 2

9i

3 11i

.

2

3i

(2

3i)(2 3i)

4

9i 2

13