ФЭИС_I_сем_II_часть

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Брестский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

а) x2 + 2xy − y2 = a2 ;

.pdf

Скачиваний:

Добавлен:

01.03.2016

Размер:

684.98 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

По условию x =1, тогда:

∆y(1) = f (1+ ∆x) −f (1) = 2(1+ ∆x)3 + 5(1+ ∆x)2 −3(1+ ∆x) +1−(2 + 5 −3 +1) =

=2(1+ 3∆x + 3∆x2 + ∆x3 ) + 5(1+ 2∆x + ∆x2 ) −3 −3∆x − 4 =

=(2 + 5 −3 − 4) + ∆x(6 +10 −3) + ∆x2(6 + 5) + 2∆x3 =13∆x +11∆x2 + 2∆x3.

Найдем дифференциал функции:

dy (1) = y′(1)dx ; y′ = 6x2 +10x −3; y′(1) = 6 +10 −3 =13 ; dy(1) =13∆x .

Итак, ∆y (1) =13∆x +11∆x2 + 2∆x3 , dy(1) =13∆x .

Если ∆x =1, то ∆y =13 +11+ 2 = 26, а dy =13.

Если ∆x = 0,1, то ∆y =1,3 + 0,11+ 0,002 =1,412, а dy =1,3 .

При малых ∆x ∆y ≈ dy .

Пример 14. Найти дифференциал функции y = 2x 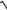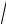49 − x2 + 492 arcsin 7x

при произвольных значениях аргумента и его приращения. Решение. Найдем производную заданной функции.

	1			x		−2x		49		1
y′ =	1	49 − x2	+	x		−2x	+	49		1		=	49 − x2 .
	2			2				2
	2			2	2 49 − x2			2			x2
									7 1	−
									7 1	−	49
											49

Тогда dy = 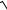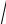49 − x2dx.

Ответ: dy =

49 − x2dx.

Пример 15. Вычислить приближенное значение arcsin0,51.

Решение.

Воспользуемся

формулой

y (x0 + ∆x) ≈ y (x0 )+ y′(x0 )∆x . В

качестве x0

возьмем x0 = 0,5 и ∆x = 0,01.

′

(arcsin x)

1− x2 .

′

∆x.

Тогда arcsin(x0 + ∆x) ≈ arcsin x0 +(arcsin x)x

Получим

π +

0,01

= π + 0,02

arcsin0,51≈ arcsin0,5 +

0,01=

1−0,25

0,5 3

= 0,524 + 0,012 = 0,536.

Ответ: 0,536.

Пример 16. Вычислить приближенное значение площади круга, радиус которого равен 3,03 м.

Решение. Известно, что площадь круга S = π R2. Пусть R = 3 , ∆R = 0,03. Тогда ∆S ≈ dS = 2π R ∆R = 2π 3 0,03 = 0,18π. Следовательно, пло-

щадь круга радиуса 3,03 м равна

S = π 3,032 ≈ π 32 + 0,18π = 9,18π ≈ 28,84(м2 ).

Ответ: 28,84 м2.

Задания для аудиторной работы

77. Найти приращение ∆y

и дифференциал dy

функции y = 5x + x2

при

x = 2 и ∆x = 0,001.

78. Найти дифференциалы функций:

x2 −1

1) y = x4 + 4x3 + 6x2 + 4x ;

y =

;

3) y = x3 + 6x2 ;

4) y = x tg3x ;

y =

+(arcsin x)2 ;

arctg x

6) y = ln(x + 4 + x2 );

y =

1− x

79. Найти дифференциалы функций, заданных неявно:

1) (x + y)2 (2x + y)3 =1;

−

y = e y .

80. Найти приближённое

значение

функции

y = x3 − 4x2 + 5x + 3

при

x =1,03 с точностью до двух знаков после запятой.

81.Насколько, приблизительно, увеличится объём шара, если его радиус R =15 см удлинится на 2 мм?

82. Найти приближённое значение 4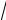17 с точностью до двух знаков после запятой.

Задания для индивидуальной работы

83. Найти приращение ∆y и дифференциал dy функции y =1− x3 при

x=1 и ∆x = − 31 .

84.Даны функция y = x3 − 2x2 + 2 и точка x0 =1. Для любого приращения независимой переменной ∆x выделить главную часть приращения функции. Оценить абсолютную величину разности между приращением функции и её дифференциалом в данной точке, если: а) ∆x = 0,1; б) ∆x = 0,01. Сравнить эту разность с абсолютной величиной дифференциала функции.

85.Найти дифференциал функций:

x +1

y = xarctgx −ln 1+ x

;

y = cos

;

y = ctg(3x2 +ln6x);

y =10tg

;

8 th

y =

;

y = sh3 4x arccos

;

−

8 th

y = th2

arcctg3x2 ;

y = cth4 2x arcsin7x2 .

86. Найти дифференциалы следующих функций, заданных неявно:

87.С помощью дифференциала приближённо (с точностью до двух знаков после запятой) вычислить данные величины:

1)	41,2 ;					2)	3 26,19 ;			3)		arcsin0,6;
4)	4				;	5)	e0,2 ;			6)		lg11;
4)	4	16,64			;	5)	e0,2 ;			6)		lg11;
			2				2,9							′
7)	ln(e			+ 0,2);		8)		;		9)			lntg 47°15 .

							2,92 +16
							2,92 +16
88. Найти приближённое значение функции									y = 3	1	− x			при x = 0,1	с точ-
										1	+ x

ностью до двух знаков после запятой.


89. Вычислить	приближённое	значение функции y = x2 −7x +10 при
x = 0,98 с точностью до двух знаков после запятой.
Ответы: 80.	5,00. 82. 2,03.	84. а) ε =\| ∆y −dy \|= 0,011,	ε 100%		=11%,
Ответы: 80.	5,00. 82. 2,03.	84. а) ε =\| ∆y −dy \|= 0,011,		dy	=11%,
				dy

б) ε = 0,000101, ε 100%dy =1,01%.

8. Производные и дифференциалы высших порядков

Производной второго порядка (второй производной) функции y = f (x)

называется производная ее производной, т.е. y′′ = (f ′(x))′ = f ′′(x).

Производные высших порядков (третья, четвертая и т.д.) находятся последовательным дифференцированием функции:

y′′′ = (f ′′(x))′, y(4) = (f ′′′(x))′, , y(n) = (f (n−1)(x))′.

Если функция y = y (x) задана параметрически системой уравнений

x = x(t),

y = y(t),

′	′′	′′′
то производные yx,	yxx,	yxxx, находятся по формулам:

′

′ ′

′′

′

y (t)

′′

(yx )t

′′′

(yxx )t

, .

′

yxx

′

yxxx

′

x (t)

Дифференциал второго порядка определяется как дифференциал от дифференциала первого порядка, т.е. d2y = d(dy). Аналогично определяются дифференциалы высших порядков: d3y = d(d2y), ,dny = d(dn−1y).

Если y = f (x),

где х – независимая переменная, то дифференциалы

высших порядков вычисляются по формулам:

′′

′′′

y = y

(n−1)

= y (dx) ;

y = y (dx) ; ;

(dx) .

Пример 17. Найти производные всех порядков функции y = x5 − 4x3 + 7x 2 −8.

Решение.

y′ = 5x4 −12x2 +14x,

y′′ = 20x3 − 24x +14,

y′′′ = 60x2 − 24,

y(4) =120x,

y(5) =120,

y(6) = y(7) = = 0.

Пример 18. Найти y(n)(x) функции y = ln x.

Решение. Находим последовательно производные данной функции.

y′ =

= x−1, y′′ = (−1)x−2,

y′′′ = (−1)(−2)x−3,

y(−4) = (−1)(−2)(−3)x−4, ,

(n)

−n

n−1

−n

(−1)n−1(n −1)!

= (−1)(−2)(−3) (−n +1)x

= (−1) (n −1)! x

Ответ:

(n)

(−1)n−1(n −1)!

Пример 19. Найти первую и вторую производные функции, заданной

параметрически x = lnt,

y =1 t .

′

Решение. Первая производная находится по формуле y′x =

y (t)

′

x (t)

′

= −

y (t) = −

x (t) =

yx =

′ ′

Вторая производная:

y′′xx = d

= (yx )t

: 1 =

dx2

xt′

Ответ: y′x = −1 t ; y′′xx =1 t .

Пример 20. Показать,

что функция y = ex + 3e2x удовлетворяет урав-

нению y′′′ − 6y′′ +11y′ − 6y = 0.

Решение. Находим первую, вторую и третью производные данной

функции и подставляем их в уравнение.
y′ = ex + 6e2x,	y′′ = ex +12e2x,	y′′′ = ex + 24e2x,
(ex + 24e2x ) − 6(ex +12e2x ) +11(ex + 6e2x ) − 6(ex + 3e2x ) =
= ex (1− 6 +11− 6) + e2x (24 −72 + 66 −18) = 0.
Итак, функция y = ex +3e2x	удовлетворяет уравнению y′′′−6y′′+11y′−6y = 0.

Пример 21. При прямолинейном движении материальной точки зави-

симость пути от времени определяется уравнением s = 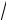t. Найти уско-

рение движущейся точки в конце четвертой секунды.

Решение. Первая производная пути по времени определяет скорость движения, а вторая производная – ускорение.

		′			1				′	1		1	1
					1					1		1	1
												2)
s(t) =	t, v(t) = s (t)		=		2 t	,	a(t) = v (t) =			2	(−	2)		t3	,
		a(4) = −			1		= −	1	(м / c2 ).
								32
				4 43
				4 43

Ответ: − 321 м / c2.

Задания для аудиторной работы

90.Найти вторую производную функции y = (1+ 4x2 ) arctg 2x .

91.Для данных функций вычислить y′′′(x0 ):

1)	y = sin2 x , x0	=	π	;	2)	y = ln(2 + x2 ), x0 = 0 ;
			2			y = ex cos x , x0 = 0 .
3)	y = arctg x , x0 =1;				4)	y = ex cos x , x0 = 0 .

92. Записатьформулыдля производныхn-гопорядка указанных функций:

1) y = ln x ;								2) y =1 x ;								3) y = 2x ;
4)	y = cos x ;							5)	y =		1			;		6)	y = e−2x ;
4)	y = cos x ;							5)	y =	2x + 5				;		6)	y = e−2x ;
										2x + 5
7)	y = xn							8)	y = xe3x ;							9)	y = ln(3 + x).
7)	y = xn			x		;		8)	y = xe3x ;							9)	y = ln(3 + x).
93. Найти y′ и y′′:
	x = (2t + 3);										2cos		2		t;					2	),
1)								2)	x =		2cos				t;	3)	x = ln(1+ t				),
1)								2)				2				3)
	y = 3t3;								y =		3sin	2		t;			y = t −arctg t;
									y =		3sin			t;

		2t	−t		2		,						2		+1),
					2								2
4)	x =							5)	x = cos(t							6)	x = arccos t,
		4t	−t4;

	y =								y = sin2 t;								y = t	−t	2	.
																	y = t	−t		.

94.Найти y′(1;1), y′′(1;1) функции, заданной неявно уравнением

x2 + 2y2 − xy + x + y = 4.

95.Найти y′ и y′′:

1) y2 = 8x ;	2)		x2	+		y2		=1;	3) y =
		5
				7
96. Найти дифференциалы второго порядка функций:
1) y = e−x3 ;	2)	y = cos5x ;							3)	y =
97. Найти дифференциалы третьего порядка функций:
1) y = sin2 2x ;	2)		y =		ln x		;		3)	y =

						x

x + arctg y .

arccos x .

x2e−x .

	Задания для индивидуальной работы
98. Для данных функций вычислить y′′′(x0 ):
1)	y = ex sin2x , x0 = 0 ;		2)	y = e−x cos x , x0 = 0 ;
3)	y = sin2x , x0 = π ;		4)	y = (2x +1)5 , x0 =1;
5)	y = ln(1+ x), x0	= 2 ;	6)	y = 1 x2ex , x0 = 0 ;
				2
7)	y = arcsin x , x0	= 0 ;	8)	y = (5x − 4)5 , x0 = 2 ;
9)	y = x sin x , x0 =	π ;	10) y = x2 ln x , x0 = 1		;
		2		3

11)	y = x sin2x , x0	= −	π	;	12)	y = x4 ln x , x0 =1;
			4					π .
13)	y = x + arctg x ,	x0 =1;			14)	y = cos2 x , x0	=	π .
								4

99. Записатьформулыдляпроизводныхn-го порядка указанных функций:

1) y = ln(5 + x2 );

2) y = e4x ;

3) y =

;

x − 7

4) y = 5x ;

5) y = e−5x ;

6) y = ln(4 + x) ;

y =

;

8) y =10x ;

9) y = cos3x .

x − 6

100. Найти y′ и y′′:

;

−2t

x =

;

+ t

x = e

x = t

;

y = e

y =

;

y =

;

+ t

x =

t2 −1;

;

lnt

;

x = 4t + 2t

x =

y =

t +1

;

y = 5t

−3t

;

−1

y = t lnt;

cost;

;

x = 5cost;

x = e

x = t

y = 4sint;

y = lnt;

y = e sint;

5cos

x = arcsint;

x = arctg t;

10)

11)

12)

= ln(1+ t2 );

y = 3sin

y =

1−t

;

3(t

−

sint);

x = sin2t;

x = 5(t − sint),

13)

14)

15)

3(1−cost);

= cos2 t;

= 5(1− cost).

101. Показать, что функция y = e2x sin5x удовлетворяет уравнению

102. Найти y′ и y′′:

y′′ − 4y′ + 29y = 0.

1) y2 = 5x − 4 ;

2) arctg y = 4x + 5y ;

3) y2 − x = cos y ;

4)	3x + sin y = 5y ;		5) tg y = 3x + 5y ;			6) xy = ctg y ;
7)	y = ey + 4x ;		8) ln y −	y	= 7;	9) y2 + x2 = sin y ;
7)	y = ey + 4x ;		8) ln y −		= 7;	9) y2 + x2 = sin y ;
				x
10) 3y = 7 + xy3 ;			11) 4sin2(x + y) = x ;			12) sin y = 7x + 3y ;
13) tg y = 4y −5x ;			14) y = 7x −ctg y ;			15) xy − 6 = cos y .
103. Вычислить значение второй производной функции в точке M1:
1)	ey + y − x = 0, M (1;0)	;			2) x3 + y3	− xy =1, M (1;1) ;
	1					1
3)	x2 + 2y2 − xy + x + y = 4, M (1;1) .
			1

104. Найти	d3y	функций, заданных неявно:
	dx3

1) y = ln(x + y) ;			2) xy = ex+y ;	3) y = cos(x + y) .

105. Найти дифференциалы первого и второго порядков функций:

1)	y = sin x ln x ;	2)	y = ctgx + sin−1 x ;	3)	x = y −arctgy ;
4)	y = (2x −3)3 ;	5)	y = 3sin(2x + 5);	6)	y = x arccos x .

106.Найти дифференциалы 1-го, 2-го и 3-го порядков функции y = x3 ln x .

107.Найти дифференциалы первого и второго порядков функции

y= (x2 +1)arctg x .

108.Найти дифференциалы второго и третьего порядков функции

y= e−3x cos2x .

9. Правило Лопиталя

Пусть функции f (x)

и ϕ(x) дифференцируемы в окрестности точки x0

′

Если

lim f (x) = lim ϕ(x) = 0 ( lim

f (x) = lim ϕ(x) = ∞), т.е. част-

ϕ (x) ≠ 0.

x→x0

f (x)

ное

в точке x0

представляет собой неопределенность вида

ϕ(x)

∞ , то lim

f (x)

′

= lim

f (x)

при условии, что существует предел от-

′

x→x

ϕ(x)

x→x

∞

ϕ (x)

ношения производных.

′

Если частное

f (x)

в точке x = x0

также имеет неопределенность вида

′

ϕ (x)

∞

′′

f (x)

или

и существует lim

, то справедлива формула

∞

x→x0 ϕ′′(x)

′

′′

lim

f (x)

= lim

(x)

′

x→x

′′

ϕ (x)

В случае неопределенностей вида (0 ∞) или (∞ − ∞) выражение под знаком предела следует преобразовать алгебраически так, чтобы полу-

чить неопределенность вида	или	∞	, и далее воспользоваться
чить неопределенность вида	или		, и далее воспользоваться
		∞

правилом Лопиталя.

В случае неопределенности вида (00 ), (∞0 ), (1∞ ) следует воспользо-

	b		lnab		blna			f (x)		lim f (x)
ваться тождеством a	b	= e	lnab	= e	blna	и свойством lim	e	f (x)	= e	x→x
ваться тождеством a		= e		= e		и свойством lim	e		= e	0 .
						x→x0

Пример 22. Вычислить пределы:

lim

x2 −1+ln x

;

lim

xe2x

;

3) lim x2

ln x ;

ex −e

x→1

x→∞ x + e4x

x→0

lim

−

;

lim (1+ x)ln x .

x→0

ex −1

x→∞

Решение. 1) Подставив х = 1 в функцию, получим неопределенность

вида

. Применим правило Лопиталя.

−1+ln x

−1

′

2x +

lim

=lim

+ln x)

=lim

−

′

x→1

→1

2) При x → ∞ получим неопределенность вида

∞

. Правило Лопита-

ля будем применять трижды.

∞

lim

xe2x

∞

= lim

e2x + 2xe2x

∞

= lim

2e2x + 2e2x + 4xe2x

∞

1+ 4e4x

16e4x

x→∞ x + e4x

x→∞

∞

→∞

= lim

+ x

∞

lim

= 0.

4e2x

x→∞

∞

4 x→∞ 2e2x

3) Подставив х = 0 в функцию, получим неопределенность вида (0 ∞). Преобразуем выражение под знаком предела и применим правило Лопи-

таля.

lim x2

ln x = (0

∞) = lim

ln x

∞

lim

= lim

= 0.

−2

x→0

x→0 x−2

∞

x→0 x

x→0

4) Подставив х=0 в функцию, получим неопределенность вида (∞ − ∞).

Приведем выражение под знаком предела к общему знаменателю.

−1− x

lim

−

= (∞ − ∞) =

lim

x(ex −1)

x→0

ex −1

x→0

Правило Лопиталя будем применять дважды:.

lim

ex −1− x

lim

ex −1

lim

= lim

x(ex −1)

2ex + xex

2 + x

x→0

x→0 ex −1+ xex

x→0

При x → ∞ получим неопределенность вида (∞0 ).

Воспользуемся

тождеством ab = elnab = eblna

lim (1+ x)ln x = (∞0 )=

x→∞

и свойством

1 ln(1+x)

lim eln x

x→∞

lim ef (x) = e

x→x0

ln(1+x)

= lim e ln x

x→∞

	lim f (x)
	x→x0	:
		:
	lim	ln(1+x)
	lim	ln x .
	= ex→∞	ln x .

Рассмотрим предел в показателе. При x → ∞ получим неопределен-

	∞	. Применим правило Лопиталя:
ность вида		. Применим правило Лопиталя:
	∞

ln(1

∞

(

x +1

lim

)

lim

=1;

ln x

∞

1 x

+ x

x→∞

x→∞ 1

lim

ln(1+x)

= e1 = e .

тогда: lim (1+ x)ln x

= ex→∞

ln x

x→∞

Ответы: 1) 3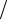e ; 2) 0; 3) 0; 4) 0,5; 5) е.

Задания для аудиторной работы

109. Найти пределы, применяя правило Лопиталя.

lim

x3 −7x2 +

+ 2

;

x3 −5x

+ 4

x→1

lim

ln(x − 4)

;

x→4 ln(ex −e4 )

lim

−

;

x→1 x −1

ln x

10)lim x1−x ;

x→1

13)lim ex3 −61− x3 ;

x→0 sin 2x

2)lim ex + e−x − 2 ;

x→0 1−cos2x

5) lim	lnsin x	;
5) lim	(π − 2x)2	;
x→π	(π − 2x)2
2

8)lim x ctgπx ;

x→0

11)lim x 4+ln x ;

x→0

14)xlim→0 x12 −ctg2x .

3)lim π − 2arctgx ;

x→∞ e3 x −1

6) lim	1		;
		−ctgx

x→0	x

9)lim sin(2x −1) tgπx ;

x→21

12)lim (x + 2x )x ;

x→∞

Задания для индивидуальной работы

110. Найти пределы указанных функций:

2x3 −7x2 + 4x

lim

− 2x2 − x + 2

;

lim

+ 4

;

x3 −7x

+ 6

4x3 −11x2 − 4x + 20

x→1

x→2

lim

x3 + 2x2

−15x −36

;

lim

x3 −12x −16

;

−10x2

+ 33x −36

x→−3 3x3 +17x2 + 21x −9

x→4 x3

lim

x3 −8x2

+ 21x −18

;

lim

−

;

2x3 −13x

+ 24x −9

−3

x→3

2 − x − 6

lim

−

;

lim

−

− x − 20

1− x2

− x3

x→5

x −5

x→1

lim

e7x −1

;

10)

lim

tg x − x

;

tg 3x

− sin x

x→0

x→0 x

− 4sin

π x

−cos x

11) lim

;

12)

lim

;

1− x

x→1

x→0 x2 − sin x2

14) lim	tg x	;
14) lim	tg 5x	;
x→π	tg 5x
2

16)lim ln x ;

x→∞ 3x

18)lim ln(x + 7) ;

x→+∞ 7x −3

20)

lim

−

;

x→0

ex −1

22)

lim

−

;

x→0

x sin x

24)

lim

x cos x − sin x

;

x→0

26)lim ln x ln(x −1);

x→1

28)lim x4e−x ;

x→∞

30)lim tg x − sin x ;

x→0 4x − sin x

32)lim ln(x + 5) ;

x→∞ 4x + 3

34)	lim		1	−	1	;


	x→0	x			sin x

36)lim(1−e2x ) ctg x ;

x→0

38)lim (arcsinx ctg x);

x→0

40) lim x sin	3	;
x→∞	x

42)	lim		lnex	;
42)	lim	1− xex		;
	x→∞	1− xex		+ e−x )cos x
44)	lim	2 −(ex		+ e−x )cos x			;
44)	lim				x4		;
	x→0				x4
46)	lim		π − 2arctgx			;
	x→∞				1
			ln 1+
			ln 1+
					x

15)lim ex ;

x→∞ x5

17) lim	π x	;

x→0 ctg(πx 2)

19)lim 1−cos7x ;

x→0 x sin7x

21)	lim		x		−	π	;


	x→π2	ctg x				2cos x
23)	lim	x sin		3	;
	x→∞			x

25)lim (1−cos x) ctg x ;

x→0

27)lim (x ln x);

x→0

29)	lim	tg x − x	;
		2sin x + x
	x→0

31)lim tg 3x ;

x→π2 tg 5x

33) xlim ctgxπx ;

→0

35)	lim	1	−	1	;


	x→1 x −1			ln x

37)lim(x2 ln x);

x→0

39)	lim	1	−		1	;


		2(1− x )		3(1
	x→1	2(1− x )		3(1	− 3 x )

41)lim etgx −ex ;

x→0 tgx − x

	1
43) lim	e	x2	−	1	;
43) lim				−π	;
x→∞ 2arctgx2				−π

45)lim (π − 2arctgx) ln x ;

x→∞

		πx
	ctg	4
47) lim			.
	x − 2
x→2

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.20192.21 Mб12Философия ч.3-4.doc
#
01.03.2016179.2 Кб37ФКИ маленькие сокр.doc
#
01.09.2019144.38 Кб8фо заочники.doc
#
11.12.201833.3 Кб6ФР.docx
#
10.11.2019109.57 Кб7Фразы приветствие, прощание.doc
#
01.03.2016684.98 Кб21ФЭИС_I_сем_II_часть.pdf
#
13.09.2019162.3 Кб7Характеристика Хозяйства.doc
#
26.09.2019683.52 Кб5Химия экзамен 2 семестр.doc
#
01.03.2016323.3 Кб379химия.docx
#
16.04.20192.42 Mб12хотько ЖБК.docx
#
01.03.20161.75 Mб71Ценообразование методичка.pdf