
- •Тема: Границя функції неперервного аргументу.
- •Диференціальне числення функції однієї змінної. Тема: Похідна функції
- •Тема: Обчислення похідної функції
- •Тема: Похідна складеної функції Теоретичні питання
- •Тема: Диференціювання неявно та параметрично заданих функцій.
- •Тема: Диференціал функції
- •Тема: Похідні та диференціали вищих порядків
- •Тема: Теореми про середнє. Правила Лопіталя Основні означення та теореми
- •Інтегральне числення функції однієї змінної Тема: Основні методи інтегрування
- •Властивості невизначеного інтеграла
- •Таблиця основних інтегралів
- •Основні методи інтегрування
- •Тема: Інтегрування раціональних дробів
- •Інтеграли від елементарних дробів
- •Тема: Інтегрування ірраціональних виразів. Основні означення та теореми
- •Тема: Інтегрування тригонометричних функцій.
- •Інтегралів на збіжність.
- •Ознаки порівняння
- •Числові ряди
- •1.1. Знакододатні ряди
- •Необхідна умова збіжності числового ряду
- •Достатні умови збіжності знакододатних рядів
- •Зразки розв’язання задач
- •Завдання для самостійної роботи
- •1.2. Знакозмінні ряди
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •4.2.Розвинення в ряди Фур’є 2π-періодичних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Відповіді
Зразки розв’язування задач
1.
Записати у
вигляді збіжного числового ряду
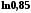 .
.
Можна
вважати, що шукана величина є значенням
функції
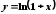 при
при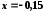 :
:
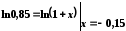 .
.
Запишемо розвинення в ряд Маклорена логарифмічної функції
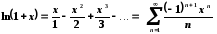 ,
,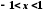 .
.
Значення
аргументу
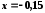 належить області збіжності наведеного
ряду, отже, шукане значення функції
можна отримати у вигляді числового ряду
підстановкою вказаного значення у
степеневий ряд:
належить області збіжності наведеного
ряду, отже, шукане значення функції
можна отримати у вигляді числового ряду
підстановкою вказаного значення у
степеневий ряд:
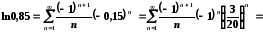
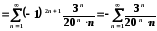 .
.
2.
Записати у
вигляді збіжного числового ряду
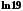 .
.
Спроба
представити шукане значення у вигляді
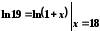 є
є
недоцільною,
оскільки
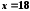 не належить області збіжності відповідного
ряду, отже, використання цього розвинення
неможливе.
не належить області збіжності відповідного
ряду, отже, використання цього розвинення
неможливе.
Запишемо аргумент функції у вигляді дробу
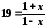 ;
;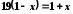 ;
;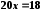 ;
;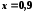 .
.
Таким чином, можна вважати, що
 .
.
Представимо логарифм дробу у вигляді степеневого ряду:
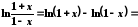
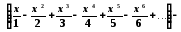
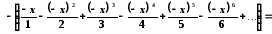
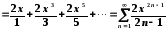 ,
,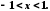
Тоді
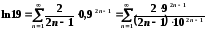 .
.
3.
Записати у
вигляді збіжного числового ряду
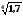 .
.
Можна
вважати, що шукана величина є значенням
функції
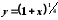 при
при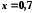 :
:
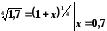 .
.
Запишемо розвинення в ряд Маклорена цієї функції.
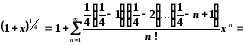
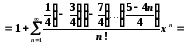
 ,
,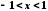 .
.
Значення
аргументу
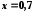 належить області збіжності наведеного
ряду, отже, шукане значення функції
можна отримати у вигляді числового ряду
підстановкою вказаного значення у
степеневий ряд:
належить області збіжності наведеного
ряду, отже, шукане значення функції
можна отримати у вигляді числового ряду
підстановкою вказаного значення у
степеневий ряд:
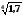
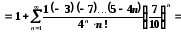
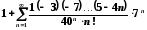 .
.
Ряд можна записати також у такій формі:
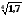
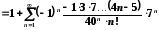 .
.
4.
Записати у
вигляді збіжного числового ряду
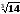 .
.
Спроба
представити шукане значення у вигляді
 є недоцільною, оскільки
є недоцільною, оскільки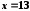 не належить області збіжності біноміального
ряду, отже, використання цього розвинення
неможливе.
не належить області збіжності біноміального
ряду, отже, використання цього розвинення
неможливе.
Порівняємо значення аргумента кореня третього степеня з відповідними (третіми) степенями натуральних чисел:
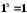 ,
,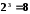 ,
,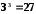 ;
;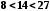 .
.
Тоді можна представити аргумент кореня у вигляді
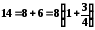 ,
,
який надає можливість скористатися табличним розвиненням:
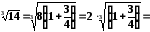
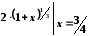 .
.
Запишемо відповідне табличне розвинення
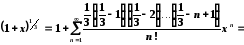
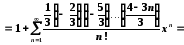
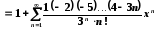 ,
,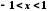 .
.
Значення
аргументу
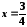 належить області збіжності наведеного
ряду, отже, шукане значення функції
можна отримати у вигляді числового ряду
підстановкою вказаного значення у
отримане розвинення:
належить області збіжності наведеного
ряду, отже, шукане значення функції
можна отримати у вигляді числового ряду
підстановкою вказаного значення у
отримане розвинення:
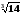
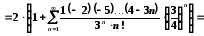
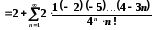 .
.
Ряд можна також записати у такій формі:

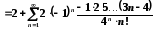 .
.
5.
Записати у
вигляді збіжного числового ряду
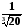 .
.
Порівняємо значення аргументу кореня третього степеня з відповідними (третіми) степенями натуральних чисел:
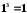 ,
,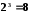 ,
,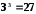 ;
;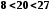 .
.
Тоді можна представити аргумент кореня у вигляді
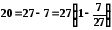 ,
,
який надає можливість скористатися табличним розвиненням:
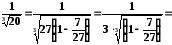
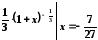 .
.
Запишемо відповідне табличне розвинення
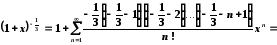
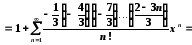
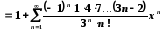 ,
,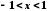 .
.
Значення
аргументу
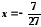 належить області збіжності наведеного
ряду, отже, шукане значення функції
можна отримати у вигляді числового ряду
підстановкою вказаного значення у
отримане розвинення:
належить області збіжності наведеного
ряду, отже, шукане значення функції
можна отримати у вигляді числового ряду
підстановкою вказаного значення у
отримане розвинення:
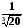
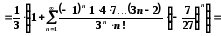
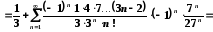
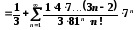 .
.
Зауваження.
Спроба записати число 20
у вигляді
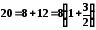 є недоцільною, оскільки отримане таким
чином значення аргументу степеневої
функції
є недоцільною, оскільки отримане таким
чином значення аргументу степеневої
функції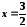 лежить за межами області збіжності
відповідного ряду.
лежить за межами області збіжності
відповідного ряду.
6.
Обчислити
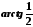 з точністю
з точністю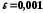 .
.
Представимо шукане значення у вигляді збіжного числового ряду.
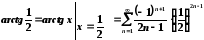 ;
;
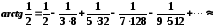
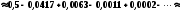
 .
.
Залишковий член цього ряду з чергуванням знаків за абсолютним значенням не перевищує першого відкинутого члена ряду, отже,
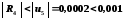 .
.
7.
Обчислити
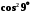 з точністю
з точністю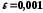 .
.
Представимо шукане значення у вигляді збіжного числового ряду.
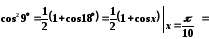
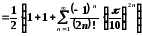
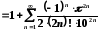 ;
;
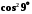

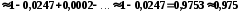
Залишковий член цього ряду з чергуванням знаків за абсолютним значенням не перевищує першого відкинутого члена ряду, отже,
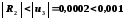 .
.
Зауваження. При обчисленні значень тригонометричних функцій використовується радіанна міра аргументів.
8.
Обчислити
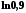 з точністю
з точністю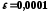 .
.
Представимо шукане значення у вигляді збіжного числового ряду.
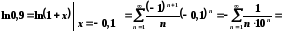
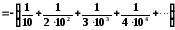 .
.
Цей ряд на відміну від попередніх є знакосталим, тому необхідно застосувати іншу методику оцінки залишкового члена ряду.
Припустимо,
що для забезпечення заданої точності
треба залишити
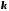 членів ряду. Тоді залишковий член ряду
відповідає умові
членів ряду. Тоді залишковий член ряду
відповідає умові
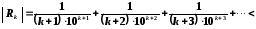
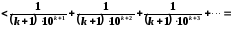
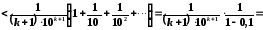
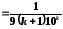 .
.
Оберемо
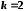 .
Тоді
.
Тоді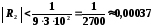 .
Очевидно, що обраної кількості членів
ряду недостатньо для досягнення заданої
точності.
.
Очевидно, що обраної кількості членів
ряду недостатньо для досягнення заданої
точності.
Візьмемо
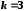 .
В цьому випадку
.
В цьому випадку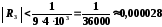 ,
тобто
,
тобто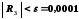 .
.
Тоді
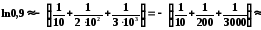
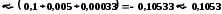 .
.
8.
Обчислити
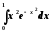 з точністю
з точністю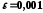 .
.
Запишемо
розвинення у ряд Маклорена підінтегральної
функції
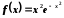 .
.
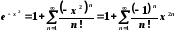 ;
;

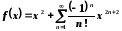 .
.
Цей ряд збігається на всій множині дійсних чисел.
Тоді
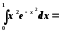
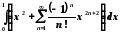 =
=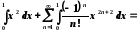
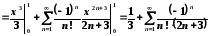 .
.

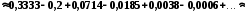
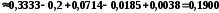 .
.
Залишковий член цього ряду з чергуванням знаків за абсолютним значенням не перевищує першого відкинутого члена ряду, отже,
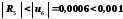 .
.
9.
Обчислити
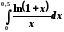 з точністю
з точністю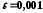 .
.
Підінтегральна
функція
 не визначена при
не визначена при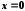 ,
але
,
але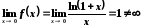 ,
отже, функція є інтегровною на проміжку
,
отже, функція є інтегровною на проміжку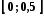 .
Запишемо розвинення у ряд Маклорена
підінтегральної функції .
.
Запишемо розвинення у ряд Маклорена
підінтегральної функції .
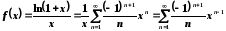 .
.
Отриманий
ряд збігається, якщо
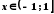 ,
отже його можна почленно інтегрувати
на проміжку
,
отже його можна почленно інтегрувати
на проміжку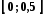 .
.
Тоді
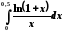
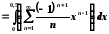
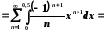
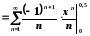
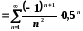 ;
;

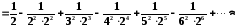
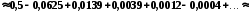
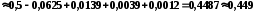 .
.
Залишковий член цього ряду з чергуванням знаків за абсолютним значенням не перевищує першого відкинутого члена ряду, отже,
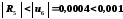 .
.
