
Lection15
.docxЛекция 15. «Дифференцирование функции нескольких переменных»
-
Градиент функции двух переменных и производная по направлению.
Определение. Градиентом функции

называется вектор
 .
.
Иначе, этот вектор может быть записан следующим образом:

или

или

Как видно из определения градиента функции, компонентами вектора градиента являются частные производные функции.
Пример. Вычислить градиент функции

в точке A(2,3).
Решение. Вычислим частные производные функции.


В общем виде градиент функции имеет вид:
 =
=

Подставим координаты точки A(2,3) в выражения частных производных


В градиент функции в точке A(2,3) имеет вид:
 =
=

Аналогично можно определить понятие градиента функции трех переменных:
Определение. Градиентом функции от трех переменных

называется вектор

Иначе, этот вектор может быть записан следующим образом:

Определение производной по направлению.
Пусть задана функция двух переменных

и произвольный вектор

Рассмотрим приращение этой функции, взятое вдоль данного вектора

Т.е.
вектор
 коллинеарный по отношению к вектору
коллинеарный по отношению к вектору
 .
Длина приращения аргумента
.
Длина приращения аргумента

Производной по некоторому направлению называется предел отношения приращения функции вдоль данного направления на длину приращения аргумента, когда длина приращения аргумента стремиться к 0.

Формула для вычисления производной по направлению.
Исходя из определения градиента, производную функции по направлению, можно посчитать следующим образом.
Пусть

некоторый вектор. Вектор с тем же направлением, но единичной длины назовем

Координаты этого вектора вычисляются следующим образом:


Из
определения производной по направлению
 ,
производная по направлению
,
производная по направлению
 может быть вычислена по следующей
формуле:
может быть вычислена по следующей
формуле:

Правая часть этой формулы представляет собой скалярное произведение двух векторов

И

Поэтому, производную по направлению можно представить в виде следующей формулы:

Из этой формулы следует несколько важных свойств вектора градиента.
-
Производная в данной точке по направлению вектора S имеет наибольшее значение, если направление вектора S совпадает с направлением градиента; это наибольшее значение производной равно |
 |.
|. -
Производная по направлению вектора, перпендикулярного к вектору
 равна нулю.
равна нулю.
Первое свойство градиента следует из того очевидного факта, что скалярное произведение двух векторов принимает наибольшее значение, когда вектора совпадают по направлению. Второе свойство следует из того, что скалярное произведение перпендикулярных векторов равно нулю. Кроме того, из первого свойства следует геометрический смысл градиента – градиент это вектор, вдоль направления, которого производная по направлению наибольшая. Так как производная по направлению определяет тангенс угла наклона касательной к поверхности функции, то градиент направлен вдоль наибольшего наклона касательной.
Пример 2. Для функции (из примера 1)

Вычислить
производную по направлению

в точке A(2,3).
Решение.
Для вычисления производной по направлению
надо вычислить вектор градиента в
указанной точке и единичный вектор
направления
 (т.е.
нормализовать вектор
(т.е.
нормализовать вектор
 ).
).
Вектор градиента был вычислен в примере 1:

Вычисляем единичный вектор направления:

Вычисляем производную по направлению:

#2. Максимум и минимум функции нескольких переменных.
Определение.
Функция

Имеет
максимум в точке
 (т. е. при
(т. е. при
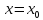 и
и
 ),
если
),
если

для
всех точек
 ,
достаточно близких к точке
,
достаточно близких к точке
 и отличных от нее.
и отличных от нее.
Определение.
Совершенно аналогично говорят, что
функция

Имеет
минимум в точке
 (т. е. при
(т. е. при
 и
и
 ),
если
),
если

для
всех точек
 ,
достаточно близких к точке
,
достаточно близких к точке
 и отличных от нее.
и отличных от нее.
Максимум и минимум функции называются экстремумами функции, т. е. говорят, что функция имеет экстремум в данной точке, если эта функция имеет максимум или минимум в данной точке.
Например, функция

Имеет очевидный минимум z = -1 при x = 1 и y = 2.

Функция

Имеет
максимум в точке
 при x
= 0 и y
= 0.
при x
= 0 и y
= 0.

Теорема. (необходимые условия экстремума).
Если
функция
 достигает экстремума при
достигает экстремума при
 ,
,
 ,
то каждая частная производная первого
порядка от z
или обращается в нуль при этих значениях
аргументов, или не существует.
,
то каждая частная производная первого
порядка от z
или обращается в нуль при этих значениях
аргументов, или не существует.
Замечание. Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции. Можно привести примеры функций, которые в некоторых точках имеет нулевые частные производные, но не имеет экстремума в этих точка.
Пример. Функции, которая имеет нулевые частные производные, но не имеет экстремума.

В
точке
 .
.
В самом деле:



Достаточные условия экстремума.
Теорема.
Пусть в некоторой области, содержащей
точку

 ,
,
 функция
функция
 имеет непрерывные
частные производные до третьего порядка
включительно; пусть, кроме того, точка
имеет непрерывные
частные производные до третьего порядка
включительно; пусть, кроме того, точка
 является
критической точкой функции
является
критической точкой функции
 ,
т.е.
,
т.е.

Тогда
при
 ,
,

-
 имеет максимум,
если
имеет максимум,
если

-
 имеет минимум,
если
имеет минимум,
если

-
 не имеет ни
минимума, ни максимума, если
не имеет ни
минимума, ни максимума, если

-
 может иметь
экстремум, а может и не иметь - требуется
дополнительное исследование, если
может иметь
экстремум, а может и не иметь - требуется
дополнительное исследование, если

Пример 3.2. Исследовать на максимум и на минимум функцию

Решение.
-
Найдем критические точки, т.е. точки, в которых первые частные производные равны нулю или не существуют.
Сначала вычисляем сами частные производные.


Приравниваем частные производные нулю и решаем следующую систему линейных уравнений
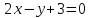
 = 0
= 0
Умножаем второе уравнение на 2 и складываем с первым. Получится уравнение только от y.

Находим
 и подставляем
в первое уравнение
и подставляем
в первое уравнение

Преобразуем

Находим

Следовательно,
точка ( )
является критической.
)
является критической.
-
Вычислим вторые производные второго порядка и подставим в них координаты критической точки.


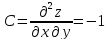
В нашем случае, подставлять значения критических точек не надо, так как вторые производные являются числами.
В итоге имеем:

Следовательно, найденная критическая точка, является точкой экстремума. Более того, так как

то эта точка минимума.
