Lection19

Лекция 19. Определенный интеграл

#1. Задача, приводящая к понятию определенного интеграла.

Рассмотрим задачу нахождения площади фигуры, образованной графиком некоторой функции на отрезке [a, b], вертикальными линиями , и осью OX.

Как видно из рисунка, площадь фигуры, образованной графиком функции на отрезке [a, b]. Не может быть вычислена непосредственно, так как график представляет собой кривую линию. Для того, чтобы вычислить площадь, разобьем отрезок [a, b] на несколько отрезков. На каждом отрезке разбиения вычислим минимальное значение функции и максимальное значение функции. Минимальные значения обозначим , а максимальные . Можно составить две суммы:

Эти суммы имеют специальные названия, а именно:

-нижняя интегральная сумма; -верхняя интегральная сумма.

Очевидно соотношение между этими суммами:

Значение площади находится между значениями этих сумм:

В качестве приближенного значения площади можно взять их среднее арифметическое.

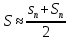
В общем случае, такой подход дает приближенное значение площади. Для того, чтобы более точно посчитать площадь, нужно увеличить число отрезков разбиения и вычислять не только минимальные и максимальные значения функции, но и значения функции в центральных точках отрезков разбиения.

Замечание. Количество отрезков разбиения не является определяющим фактором для вычисления площади с большей точностью. Определяющим фактором является длины отрезков разбиения.

#2. Определение определенного интеграла.

Пусть функция определена и непрерывна на отрезке . Разобьем этот отрезок на – отрезков разбиения:

,

где .

Точки с абсциссами называются точками разбиения. На каждом из отрезков разбиения выберем внутри отрезка некоторую произвольную точку. Эти внутренние точки обозначим как . Вычислим в этих точках значения функции .

Составим следующую сумму:

Эта сумма называется интегральной суммой. Более кратко эту сумму можно записать так

Введем следующее обозначнние для длин отрезков разбиения:

В этих определениях интегральную сумму можно записать в виде:

Разбивая отрезок на разное число отрезков разбиения, выбирая разные внутренние точки и составляя подобные суммы, мы будем получать различные интегральные суммы.

Введем еще одно вспомогательное определение: - длина максимального отрезка разбиения. Последовательность интегральных сумм можно рассматривать как зависящую именно от этого параметра – длины максимального отрезка разбиения. Устремим к нулю. Как поведет себя последовательность интегральных сумм?

Определение 1. Если при любых разбиениях отрезка , таких, что: a) длина максимального отрезка разбиения стремиться к нулю () при ; b) при любом выборе внутренних точек последовательность интегральных сумм имеет конечный предел – число S, то это число называется определенным интегралом функции на отрезке .

(*)

Число называется нижним пределом интеграла, - верхним пределом интеграла. Отрезок называется отрезком интегрирования, х - переменной интегрирования.

Определение 2. Если для функции на отрезке существует предел (*), то функция называется интегрируемой на отрезке .

Замечание. Из определения определенного интеграла следует, что величина определенного интеграла зависит от функции и пределов интегрирования, но не зависит от переменной, которая используется в записи интеграла, т.е.

Замечание. Верхняя и нижняя интегральные суммы являются частными случаями интегральной суммы, поэтому, в случае интегрируемости функции, для них верно равенство (*).

Замечание. Из определения определенного интеграла и первого параграфа лекции следует, что интеграл от функции на некотором отрезке [a, b] численно равен площади криволинейной трапеции, ограниченной графиком функции на отрезке [a, b], вертикальными прямыми , и осью OX.

Функции, которые могут быть проинтегрированы.

Теорема. Если функция непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

Так как функции, задаваемые аналитически (формулами), непрерывны в своих областях определения, то такие функции интегрируемы на отрезке, не содержащем точек разрыва.

#3. Свойства определенного интеграла.

При определении определенного интеграла предполагалось, что В случае, если будем считать, что

Другими словами, если поменять пределы интегрирования местами, то надо вынести знак «-» перед интегралом.

Если пределы интегрирования равны (a=b), то интеграл равен 0.

Свойство 1. Постоянный множитель можно выносить за знак интеграла.

Свойство 2. Интеграл от суммы (разности) двух и более функций равен сумме (разности) интегралов от этих функций.

Свойство 3. Если на отрезке [a, b] функции и удовлетворяют условию

то такому же условию удовлетворяют значения интегралов:

Свойство 4. Если на отрезке [a, b] функция удовлетворяет условиям

то

Свойство 5 (теорема о среднем). Если на отрезке [a, b] функция непрерывна, то на этом отрезке найдется точка , которая удовлетворяет условиям

Свойство 6. Для любых трех чисел a, b,c имеет место равенство

#3. Вычисление определенного интеграла. Свойство Ньютона-Лейбница.

Рассмотрим определенный интеграл 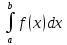. Пусть в этом интеграле нижний предел будет постоянным, а верхний предел меняется. Для каждого значения верхнего предела будем иметь собственное значение интеграла. Другими словами имеем следующую функцию

Заметим, что внутри интеграла мы можем использовать любую переменную.

Функция Ф(х) называется интегралом с переменным верхним пределом.

Имеет место следующая теорема.

Теорема. Если функция 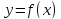непрерывная функция на отрезке и то имеет место равенство:

Иными словами, производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела (при условии, что подынтегральная функция непрерывна).

Эта формула связывает понятие определенного интеграла с понятием неопределенного интеграла (множеством первообразных от подынтегральной функции), так как интеграл с переменным верхним пределом является первообразной от подынтегральной функции.

Теорема (Формула Ньютона-Лейбница). Если функция непрерывна на отрезке и функция 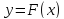ее первообразная (т.е. ), то имеет место

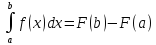
Эта формула является основной для вычисления определенных интегралов.

Пример. Вычислить определенный интеграл

Пример. Вычислить определенный интеграл

#5. Замена переменных в определенном интеграле.

Теорема. Пусть дан интеграл где функция непрерывна на отрезке .

Введем новую переменную по формуле

Если выполняются следующие условия:

1. 

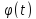2. Функции и непрерывны на отрезке

3. Функции определена и непрерывна на отрезке

то имеет место равенство:

Пример. Вычислить определенный интеграл