Lection12

Лекция №12

Дифференциальные характеристики функции.

1. Дифференциал функции.

Определение дифференциала.

Рассмотрим определение производной функции, как предел отношения приращения функции к приращению аргумента, при стремлении приращения аргумента к 0.

Из этого определения следует, что отношение приращения функции к приращению аргумента равно производной пдюс бесконечно малая величина

где , при

Выделим приращение функции

Получается, что приращение функции состоит из двух частей - слагаемых. Первая часть- линейная (относительно 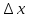) равна произведению производной функции на приращение аргумента, вторая часть бесконечно малая, которой в расчетах можно пренебречь.

Дифференциалом функции называется линейная часть приращения функции т.е. произведение производной функции на приращение аргумента.

Заметим, что для функции

ее производная равна 1, поэтому дифференциал равен приращению, поэтому дифференциал аргумента равен приращению аргумента т.е.

Окончательная формула для дифференциала

Замечание. Из этой формулы следует, что производная равна отношению дифференциала функции к дифференциалу аргумента. Это и обьясняет запись производной в виде

Замечание. Так как геометрический смысл производной это тангенс угла наклона касательной, то геометрический смысл дифференциала это приращение касательной к функции в точке.

Применение дифференциала.

Пример. Найти дифференциал и приращение функции

в общем случае и при

Решение. Вычислим приращение функции

Вычислим дифференциал функции

Заметим, что приращения и дифференциал функции отличаются на величину

Подставим значения

Величины приращения функции и дифференциал отличаются на величину 0.01, которой в расчетах можно пренебречь.

Пример. Вычислить .

В нашем случае

Подставляем

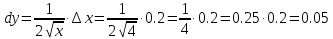
Если посчитать значение на калькуляторе, то

Свойства дифференциала.

Задача нахождения дифференциала равносильна нахождению производной функции. Поэтому многие правила для вычисления производной переносятся на дифференциал.

Утверждение.

Дифференциал суммы (разности) функций равен сумме (разности) дифференциалов этих функций.

Дифференциал произведения двух функций можно вычислить по формуле

Дифференциал отношения двух функций можно вычислить по формуле

2. Производные высших порядков.

Если функция

дифференцируема на некотором интервале, то производная от этой функции

также может быть дифференцируема на некотором интервале, т.е. может быть вычислена производная от производной. Такая производная называется производной 2-го порядка

Заметим, что обычная производная называется производной 1-го порядка.

Пример. Вычислить производную 2-го порядка от фунции

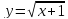
Сначала вычисляем обычную производную, т.е. производную 1-го порядка.

Вычисляем производную от полученной функции.

Полученный результат есть производная второго порядка.

Аналогично, можно ввести понятие производной третьего порядка, как производной от производной второго порядка.

В общем случае, производная n-го порядка определяется как производная от производной предыдущего (n-1) порядка, т.е.

Заметим, что при определении производной, порядок производной берется в скобки чтобы отличить порядок производной от порядка степени.

3. Теоремы Ферма, Ролля, Лагранжа, Коши.

Теорема Ферма. Если функция у = f (х), определенная в интервале (а ; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.

Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс (рис.).

c

Теорема Ролля. Если функция у = f (х), непрерывная на отрезке [а ; b] и дифференцируемая в интервале (а ; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а ; b) существует такая точка с, что f ′(с) = 0. Геометрически эта теорема означает следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс

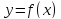
Напомним, что геометрический смысл производной это тангенс угла касательной. Равенство нулю производной означает, что тангенс угла наклона касательной равен нулю, т.е. касательная параллельна оси OX.

Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [а ; b] и дифференцируема в интервале (а ; b), то в этом интервале найдется такая точка с, что

Эта теорема имеет простой геометрический смысл. Выражение слева – это тангенс угла наклона секущей (угол ), выражение справа – это тангенс угла наклона касательной. Следовательно, если условия теоремы выполняются, на графике функции у = f (х) между точками а и найдется такая внутренняя точка , что касательная к графику в точке параллельна хорде (а ; b).

угол

Формулу в теореме Лагранжа можно переписать в следующем виде

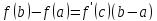
Из этой формулы следует.

Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.

Теорема Коши. Если функции f (х) и g (х):

1) непрерывны на отрезке [а ; b];

2) дифференцируемы в интервале (а ; b);

3) g'(x) ≠ 0 в этом интервале,

то в интервале (а ; b) существует такая точка с, что имеет место равенство

4. Раскрытие неопределенностей. Правило Лопиталя.

Теорема. Правило Лопиталя.

Пусть функции и удовлетворяют условиям теоремы Коши и в точке , обращаются в ноль, т.е. .

Тогда, если существует предел отношения производных в точке

то, существует предел отношения функций в точке

Причем, они равны

Замечание. Правило Лопиталя используется для раскрытия неопределенностей

при вычислении пределов. Это правило говорит о том, что, в случае неопределенности, предел отношения функция можно заменить пределом отношения производных.

Пример. Вычислить предел

Правило Лопиталя можно применять несколько раз.

Пример. Вычислить предел

Правило Лопиталя можно применять при x.

Пример. Вычислить предел

Правило Лопиталя может раскрыть неопределенность .

Пример. Вычислить предел