Lection11

Лекция №11

Дифференцирование функций.

1. Примеры вычисления производных простейших функций.

Вычислить производную функции

Вычислить производную функции

Вычислить производную функции

Вычислить производную функции

Вычислить производную функции

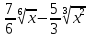
2. Производная суперпозиции функций (или сложной функции).

Определение. Если функцию

можно представить в виде комбинации двух функций

т.е.

то, функция

называется суперпозицией двух функций

Функция называют внешней функцией. Функцию называют внутренней функцией или промежуточной функцией.

Пример.

Пример.

Пример.

Утверждение. Пусть задана суперпозиция двух функций.

Если функция

имеет производную в точке , а функция

имеет производную в точке 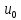, причем

то, функция

имеет производную в точке , причем

Или, в более простой форме

Таблица производных для суперпозиции функций ().

Функция	Производная

Пример.

Пример.

Пример.

3. Обратная функция и ее производная.

Определение возрастающей функции. Функция

называется монотонно возрастающей на некотором интервале, если для любых двух точек этого интервала имеет место соотношение:

если

то

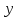
Определение убывающей функции. Функция

называется монотонно убывающей на некотором интервале, если для любых двух точек этого интервала имеет место соотношение:

если

то

Замечание. В общем случае функция может на отдельных интервалах быть монотонно возрастающей, а на других монотонно убывающей.

Функция называется монотонной, если она или монотонно возрастающая или монотонно убывающая.

Монотонная функция

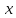обладает тем свойством, что любому значению функции существует единственное соответствующее значение аргумента . А это значит, что можно рассматривать функцию зависимости аргумента , от значения функции т.е. функцию

Определение. Функция

называется обратной к функции

если

Пример. Функция

будет обратной к функции

В самом деле

Утверждение. Если для функции

существует обратная функция

которая в рассматриваемой точке имеет производную

то в соответствующей точке , функция имеет производную

Пример. В качестве иллюстрации работы этой формулы, выведем формулу для производной арксинуса.

Решение.

Обратная функция

Ее производная

В итоге

4. Функция, заданная неявно и ее производная.

Функция задана неявно

Пример.

Очевидно, что если переменную можно выразить через переменную путем преобразований, то получится обычное – явное задание функции. Но в общем случае это сделать нельзя.

Для вычисления производной необходимо дифференцировать исходное уравнение. А затем выразить значение производной через остальные компоненты.

Пример. Посчитать производную окружности, заданной уравнением

Решение.

5. Функция, заданная параметрически и ее производная.

Пусть заданы две функции

Для каждого значения переменной , можно вычислить значения переменных и . Каждому значению переменной соответствует точка с координатами (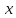,). Поэтому, когда переменная принимает все значения из отрезка, то точка (,) описывает некоторую кривую на плоскости. Некоторые кривые могут быть заданы только параметрически.

Пример. Циклоида – кривая, которую описывает точка на окружности, когда окружность катится по прямой линии.

Известные кривые также могут быть заданы параметрически

Пример. Окружность с центром в начале координат и радиусом :

Пример. Эллипс

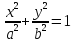
Утверждение. Если функция задана параметрически

Если обе функции дифференцируемы по переменной , то дифференцируема и функция от , причем имеет место формула.

Пример. Вычислить производную циклоиды

Решение.