Lection07

Лекция №7

Кривые и поверхности второго порядка.

1. Кривые второго порядка на плоскости.

Алгебраической кривой второго порядка называется кривая линия, уравнение которой в декартовой системе координат, в общем, имеет вид:

где не все коэффициенты , и равны одновременно нулю.

Путем преобразований, уравнение кривой 2-го порядка может быть сведено к следующим трем видам кривых.

	Эллипс
	Гипербола
	Парабола

1. Эллипс – геометрическое множество точек плоскости, сумма расстояний от которых до двух точек и , называемых фокусами, есть величина постоянная , большая, чем расстояние между фокусами :

Y

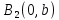
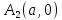X

Эллипс, заданный каноническим уравнением

симметричен относительно осей координат. Параметры и называются полуосями эллипса (большой и малой соответственно), точки , , , называются его вершинами.

Если , то фокусы находятся на оси ОХ на расстоянии

от центра эллипса О, т.е., для эллипса имеем соотношение.

Число

называется эксцентриситетом эллипса и является мерой его «сплюснутости» (при эллипс является окружностью, а при он вырождается в отрезок длиною ).

Если , то фокусы находятся на оси ОY и

1.2. Гипербола – геометрическое множество точек плоскости, модуль разности расстояний от которых до двух точек и , называемых фокусами, есть величина постоянная 2a, меньшая, чем расстояние между фокусами 2c

Гипербола, заданная каноническим уравнением:

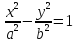
симметрична относительно осей координат. Она пересекает ось ОХ в точках и , , 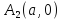- вершинах гиперболы, и не пересекает оси ОY.

Параметр называется вещественной полуосью, – мнимой полуосью.

Соотношение между фокусным расстоянием и осями для гиперболы

Число

называется эксцентриситетом гиперболы.

Прямые

называются асимптотами гиперболы.

Гипербола, заданная каноническим уравнением

или

называется сопряжённой (имеет те же асимптоты ). Её фокусы расположены на оси OY. Она пересекает ось ОY в точках , - вершинах гиперболы, и не пересекает оси ОX.

В этом случае параметр называется вещественной полуосью, – мнимой полуосью. Эксцентриситет вычисляется по формуле

Пример. Написать каноническое уравнение гиперболы, зная что:

а) расстояние между фокусами , а между вершинами ;

б) вещественная полуось равна 5, эксцентриситет .

Решение:

_а) по условию

_{Исходя из формулы}

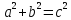
_{получаем}

Следовательно, уравнение гиперболы имеет вид

б) по условию

Находим фокусное расстояние

Находим мнимую полуось

3. Парабола – множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой

Парабола

имеет фокус

и директрису

Парабола, заданная указанным каноническим уравнением, симметрична относительно оси ОХ.

Парабола

имеет фокус

и директрису

симметрична относительно оси ОY.

Если 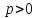, то в обоих случаях ветви параболы обращены в положительную сторону соответствующей оси, а если – в отрицательную сторону.

Пример. Написать уравнение параболы, зная, что:

а) парабола проходит через точки (0,0); (3,6) и симметрична относительно оси ОХ,

б) парабола проходит через точки (0,0); (4,2) и симметрична относительно оси ОY.

Решения.

а) Так как парабола симметрична относительно оси Х, то ее уравнение

Подставляем в это уравнение координаты точки (3,6) и получаем

Следовательно, уравнение параболы имеет вид

Можно выписать уравнение директрисы

б) Так как парабола симметрична относительно оси Y, то ее уравнение

Подставляем в это уравнение координаты точки (4,2) и получаем

Следовательно, уравнение параболы имеет вид

Можно выписать уравнение директрисы

2. Поверхности второго порядка.

Определение. Поверхностью второго порядка называется поверхность, определяемая уравнением

где –- вещественные числа, причем хотя бы одно из чисел отлично от нуля.

Рассмотрим канонические уравнения для поверхностей второго порядка и покажем, как выглядят эти поверхности

Сфера

Определение. Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром.

Т.е. любая сфера характеризуется центром – точкой и радиусом – числом . Уравнение сферы в этом случае

Пример. Найти центр и радиус сферы

По каждой переменной выделим полный квадрат

Следовательно, центр окружность , радиус равен 2.

Эллипсоид

Определение. Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид

где, – положительные числа

Область определения

При получается эллипсоид вращения.

Гиперболоиды

Однополостным гиперболоид.

Определение. Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид

где- положительные числа.

Для построения графика надо заметить, что при любом значении переменной

В сечении получается эллипс

При получается гиперболоид вращения

Двуполостным гиперболоид.

Определение. Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид

Для построения графика надо заметить, что при любом значении переменной

В сечении получается эллипс

Однако, в отличии от предыдущего, однополостного гиперболоида, правая часть не всегда положительна, а только при

При получается гиперболоид вращения

Конус

Определение. Конусом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

где- положительные числа.

Для построения графика надо заметить, что при любом значении переменной

В сечении получается эллипс

Параболоиды

Эллиптический параболоид.

Определение. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

где- положительные числа.

Для построения графика надо заметить, что при любом положительном значении переменной

В сечении получается эллипс

При получается параболоид вращения

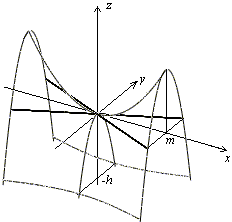
Гиперболическим параболоидом.

Определение. Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид

где- положительные числа.

Для построения графика надо заметить, что при любом значении переменной

В сечении получается гипербола

Кроме того, при , в сечении получается парабола c ветвями, направленными вверх.

А при любом значении , в сечении получается парабола с ветвями, направленными вниз.

Цилиндры.

Определение. Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые образующими.

Замечание. Если в записи уравнения поверхности нет некоторой переменной, то эта поверхность цилиндрическая.

Например, уравнение

на плоскости задает эллипс, а в пространстве цилиндрическую поверхность с направляющей равной эллипсу.

Эллиптический цилиндр.

Уравнение

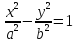
на плоскости задает гиперболу, а в пространстве гиперболический цилиндр

Уравнение

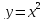
на плоскости задает гиперболу, а в пространстве параболический цилиндр