
- •Оглавление
- •Введение
- •1. Дифференциальное исчисление функций многих переменных
- •1.1. Предел и непрерывность функций многих переменных
- •1.1.1. Понятие функции многих переменных
- •1.1.2. Геометрическая иллюстрация функции двух переменных
- •1.1.3. Предел функции двух переменных в точке
- •1.1.4. Непрерывность функции двух переменных
- •1.2. Дифференцируемость функции многих переменных
- •1.2.1. Частные производные
- •1.2.2. Дифференцируемые функции
- •1.2.3. Полный дифференциал функции многих переменных
- •1.2.5. Производные высших порядков
- •1.3. Экстремум функции многих переменных
- •1.3.1. Понятие экстремума. Необходимое условие экстремума
- •1.4. Метод наименьших квадратов
- •1.4.1. Понятие эмпирической формулы
- •1.4.2. Выравнивание экспериментальных данных по прямой
- •1.4.3. Выравнивание экспериментальных данных по параболе
- •1.4.4. Выравнивание экспериментальных данных по гиперболе
- •2. Интегральное исчисление
- •2.1. Неопределенный интеграл
- •2.1.1. Определение первообразной и неопределенного интеграла
- •2.1.2. Основные свойства неопределенного интеграла
- •2.1.3. Таблица основных неопределенных интегралов
- •2.1.4. Непосредственное интегрирование. Поднесение под знак дифференциала
- •2.2. Основные методы интегрирования
- •2.2.1. Замена переменной в неопределенном интеграле
- •2.2.2. Интегрирование некоторых иррациональных функций
- •2.2.3. Интегрирование тригонометрических функций
- •2.2.4. Интегрирование по частям
- •2.2.5. Интегрирование рациональных функций
- •2.3. Определенный интеграл
- •2.3.1. Определение определенного интеграла
- •2.3.2. Необходимое условие интегрируемости функций. Классы интегрируемых функций
- •2.3.3.Свойства определенного интеграла
- •2.3.5. Замена переменной в определенном интеграле
- •2.3.7. Геометрические приложения определенного интеграла
- •2.4. Несобственные интегралы
- •2.4.2. Несобственные интегралы от неограниченных функций
- •3.1. Понятие обыкновенного дифференциального уравнения n-го порядка и его решения
- •3.2. Дифференциальные уравнения первого порядка
- •3.2.1. Понятие дифференциального уравнения первого порядка и его решения. Задача Коши. Теорема Коши. Понятие общего решения
- •3.2.4. Однородные дифференциальные уравнения первого порядка
- •3.3. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •3.3.1. Постановка задачи Коши и понятие общего решения для линейного дифференциального уравнения второго порядка
- •3.3.2. Свойства решений линейных однородных уравнений
- •3.3.3. Решение однородных линейных уравнений второго порядка с постоянными коэффициентами
- •4. Ряды
- •4.1. Числовые ряды
- •4.1.1. Понятие числового ряда и его сходимости
- •4.1.2. Простейшие свойства сходящихся рядов
- •4.1.3. Необходимый признак сходимости ряда и его следствие
- •4.1.4. Достаточные признаки сходимости рядов с неотрицательными членами
- •4.1.5. Знакопеременные ряды. Абсолютная и условная сходимость
- •4.1.6. Знакочередующиеся ряды. Признак Лейбница
- •4.2. Степенные ряды
- •4.2.1. Понятие функционального ряда и его области сходимости
- •4.2.2. Степенные ряды. Теорема Абеля
- •4.2.3. Интервал, радиус и область сходимости степенного ряда
- •4.2.4. Ряды Тейлора и Маклорена. Разложение некоторых элементарных функций в степенные ряды
- •Вопросы для повторения и тренировочные задания
- •1. Функции многих переменных
- •2а. Неопределенный интеграл
- •2б. Определенный интеграл
- •3: Дифференциальные уравнения
- •4. Ряды
- •Вопросы к экзамену
- •Литература

2.3.5. Замена переменной в определенном интеграле
Установленная выше связь определенного и неопределенного интегралов сводит, по сути дела, вычисление определенного интеграла к взятию неопределенного интеграла и подстановки соответствующих пределов интегрирования. Следовательно, все изученные ранее методы нахождения интегралов в полной мере могут быть использованы и в данном случае. В частности, справедливы следующие утверждения.
Теорема 2.16. Пусть f (x) − непрерывная на [a,b] функция, а x =φ(t) - непрерывно дифференцируемая на [α, β ] функция такая, что переменная х=φ(t) принимает все свои значения от a до b . Тогда
|
|
b |
β |
|
|
|
|
∫ f (x)dx |
′ |
(2.11) |
|
|
|
= ∫ f (φ(t)) φ |
(t)dt |
||
|
|
a |
α |
|
|
|
Таким |
образом, для |
вычисления |
определенного |
интеграла |
∫b |
f (x)dx |
нужно ввести замену х=φ (t) , где φ (t) – |
некоторая |
||
a |
|
|
|
|
|
непрерывно дифференцируемая функция, являющаяся монотонной
и найти новые пределы |
интегрирования по переменной t , решив |
|
для этого |
уравнения |
a = φ (α) , b =φ(β) . Выразив отсюда |
α =φ−1(a), |
β =φ−1(b) , имеем из (2.11) |
|
|
b |
φ −1(b) |
|
∫ f (x) dx = ∫ f (φ(t)) φ′ (t) dt . |
|
aφ −1(a)
Значит, при использовании метода замены переменной в определенном интеграле не обязательно возвращаться к исходной переменной интегрирования x , а достаточно лишь изменить пределы интегрирования.
Пример 2.18. Найти ∫1 
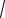 1− x2 dx .
1− x2 dx .
0
60

Решение. Выполним замену x = sin t , |
dx = cost dt, t = arcsin x . |
||||||
|
|
|
|
′ |
|
π |
|
Поскольку |
x = sin t и ее производная |
x |
= cost |
на отрезке [0, 2 ] |
|||
|
|||||||
непрерывны при изменении t от 0 до |
π , а значения x = sin t не |
||||||
|
|
|
|
2 |
|
||
выходят |
за |
пределы отрезка |
[0;1] и |
α = arcsin 0 = 0 , |
|||
β = arcsin1 = π |
, то условия теоремы 2.16 выполняются, а значит, |
||||||
|
2 |
|
|
|
|
|
|
ππ
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
sin 2t |
|
π |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
∫ 1− x |
2 |
dx |
= ∫sin |
2 |
tdt |
= ∫(1+cos 2t)dt = |
(t + |
) |
= |
|||||||||||||||||||||||||||||
|
|
|
|
2 |
|
2 |
|
0 |
|
|||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
= |
1 |
( |
π + |
sinπ |
) − |
1 (0 +0) = π . |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||
Формула замены переменной (2.11), прочитанная справа нале- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
во, позволяет сводить вычисление интеграла ∫ |
f |
(φ(x))φ |
′ |
(x)dx с по- |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
мощью подстановки φ (x) = t |
|
к вычислению интеграла |
|
∫ f ( t)dt, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
где α = φ (a), β = φ (b) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
exdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 2.19. |
Найти ∫0 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
4e2x +12ex +34 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
x |
dx |
|
|
|
|
|
|
|
|
|
x |
, |
|
|
|
|
x |
dx, |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
e |
|
|
|
= |
|
|
t = e |
|
|
|
dt = e |
|
|
|
|
|
|
= |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∫0 4e2x +12ex +34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x = 0, t = e0 =1, x =1, |
|
t = e1 = e |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
u = 2t +3, |
|
|
|
|
|
|
|
||||||||||
|
e |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
du = 2dt, |
|
||||||||||||||||||
= ∫ |
|
|
= ∫ |
|
|
|
|
= u(1)= 5, |
|
u(e)= 2e |
+3 = |
|||||||||||||||||||||||||||||
4t2 +12t +34 |
(2t + |
3)2 + 25 |
|
|
||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
2e+3 |
|
du |
|
|
1 |
|
|
|
|
|
|
|
|
u |
|
2e +3 |
|
1 |
|
|
|
2e +3 |
π |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
= 2 |
∫5 |
|
= |
|
|
|
arctg |
|
5 |
|
5 |
|
|
= |
|
(arctg |
|
|
|
− 4 ) . |
|
|
||||||||||||||||||
u2 + 25 |
|
10 |
|
|
|
|
10 |
|
5 |
|
|
|
||||||||||||||||||||||||||||
61

Пример 2.20. |
π∫dx = x |
|
π |
=π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
dx |
|
|
|
|
π |
|
|
dx |
|
|
|
|
С другой стороны, |
∫dx |
= ∫ |
|
|
|
|
|
|
=∫ |
|
|
|
|
|
= |
|||||||||
|
2 |
x +sin |
2 |
x |
|
|
2 |
x (1+tg |
2 |
x) |
||||||||||||||
|
|
|
|
0 |
|
|
|
|
0 |
cos |
|
|
0 cos |
|
|
|
||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
tgx = t, |
dt |
= |
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
|
cos |
|
x, |
|
|
= ∫ |
|
|
|
dt = 0 |
|
π = 0. |
|
|
|
|||||||
|
|
|
t |
1+t |
2 |
|
|
|
|
|||||||||||||||
x = 0, |
t = 0, x =π , |
= 0 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Такой вывод получился потому, что при замене tg x = t |
|
нару- |
||||||||||||||||||||||
шаются условия |
теоремы |
2.16: в |
точке |
t = π |
функции |
|
tg x и |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
(tg x)′ = cos12 x имеют разрыв второго рода.
2.3.6. Интегрирование по частям в определенном интеграле Теорема 2.17. Пусть функция u = u(x) и v = v(x) − непрерыв-
но дифференцируемы на [a b;] функции. Тогда имеет место фор-
мула интегрирования по частям в определенном интеграле
∫b u(x)v′(x)dx = (u |
(x)v(x)) |
|
b |
− |
∫b v(x)u′(x)dx |
(2.12) |
||||||
|
||||||||||||
a |
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2.21. Найти ∫2 |
x sin xdx = [u = x, |
du = dx, |
dv = sin xdx, |
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
π |
|
|
|
|
|
|
|||
v = −cos x]= (−x cos x) |
|
π 2 + ∫2 cos xdx = − |
π cos |
π +0 cos0 |
|
|
2 = |
|||||
|
|
|||||||||||
|
+sin x |
π0 |
||||||||||
= 0 +0 +sin π |
|
|
0 |
0 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
−sin 0 =1 |
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
62
Пример 2.22. Найти ∫e sin(ln x)dx.
1 |
|
|
|
|
|
|
|
|
|
|
|
e |
|
= sin(ln x), du = cos(ln x) |
1 |
dx, |
|
||||||
Решение. I = ∫sin(ln x)dx = u |
x |
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
dv = dx, v = x ]= x sin(ln x) |
|
π |
eπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1e |
−∫cos(ln x)dx = [u = cos(ln x), |
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
= du = −sin(ln x) 1 dx, dv = dx, |
v = x ]= xsin(ln x) |
|
eπ − x cos(ln x) |
|
eπ |
− |
|||||
|
|
||||||||||
x |
|
|
|
1 |
|
|
|
1 |
|
||
eπ |
|
|
|
|
|
|
|
|
|
||
− ∫sin(ln x)dx = eπ sin(π ) −1sin(ln1) −eπ cos(π ) +1cos(0) − I; |
|
|
|
|
|
||||||
1 |
|
|
|
1 (eπ +1). |
|
|
|
|
|
||
Значит, 2I = 0 −0 +eπ +1; |
I = |
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
2.3.7. Геометрические приложения определенного интеграла
Определенный интеграл (его конструкции составления интегральных сумм и последующего предельного перехода) может быть использован при решении геометрических, физических, экономических и других задач.
Площадь плоской фигуры
Рассмотрим функцию f (x) , непрерывную и неотрицательную на отрезке [a,b]. Можно показать, что площадь криволинейной
трапеции aAAb , понимаемая в смысле предела интегральных сумм, дающих площади описанных или вписанных в криволинейную трапецию прямоугольников, есть определенный интеграл
S = ∫a |
f (x)dx |
(2.13) |
b |
|
|
63
Если же f (x) ≤ 0 на [a,b], то функция y = − f (x) |
является неот- |
||
рицательной на [a,b], тогда ∫b (− f (x))dx = − ∫b |
f (x)dx |
выражает пло- |
|
a |
a |
|
|
щадь криволинейной трапеции в случае |
f (x) ≤ 0 знак «минус» в этом |
||
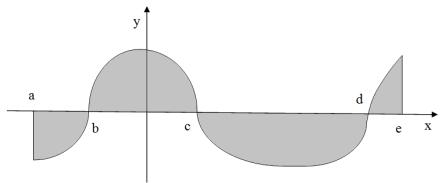
случае говорит о том, что фигура расположена ниже оси Ox . Если функция y = f (x) меняет знак на отрезке [a,b] конечное число раз, то
площадь заштрихованной фигуры (рис. 2.3) равна алгебраической сумме соответствующих определенных интегралов:
S = −∫b |
f (x)dx + ∫c |
f (x)dx −∫d |
f (x)dx + ∫e |
f (x)dx |
a |
b |
c |
d |
|
Рис.2.3.
Можно показать, что площадь плоской фигуры, ограниченной
двумя непрерывными на отрезке |
[a,b] функциями y = f (x) и |
|||||
y = g(x) ( f (x) ≥ g(x)) |
и прямыми |
x = a, x = b , |
вычисляется по |
|||
формуле |
|
|
|
|
|
|
S = ∫b ( f (x) − g(x))dx |
(2.14) |
|||||
|
|
a |
|
|
|
|
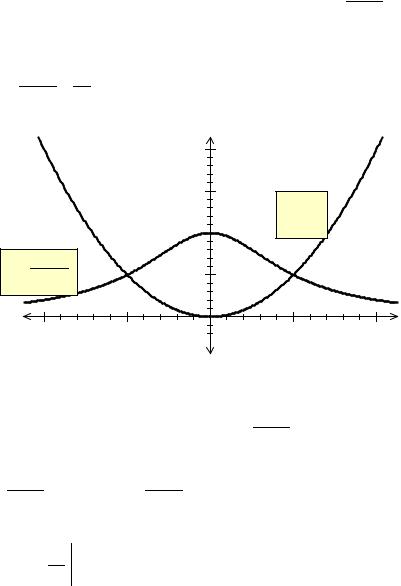
Пример 2.23. Вычислить площадь фигуры, заключенной меж- |
||||||
ду локоном Аньези y = |
|
1 |
и параболой y = |
1 x2 . |
||
1+ x2 |
||||||
|
|
|
2 |
|||
64
|
Решение. Найдем точки пересечения кривых |
y = |
|
1 |
|
и |
|||||||||||||||||||||
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ x2 |
|
||
y = |
, |
для чего решаем уравнение: |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
1 |
|
= x2 x4 |
+ x2 |
−2 = 0, x2 =1, x = ±1 |
|
|
|
|
||||||||||||||||
|
|
1+ x2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
y = x2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
1 |
|
2 |
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 + x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
-2 |
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.4. |
|
|
|
|
|
|
|
|
|
|
||||||
|
Применяя формулу (2.14) для |
f (x) = |
1 |
|
, |
g(x) = |
1 x2 |
, полу- |
|||||||||||||||||||
чаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ x2 |
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
1 |
|
|
1 |
|
2 |
1 |
|
1 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
S = |
−∫1(1+ x2 − |
2 x |
|
dx) = 2∫0 (1+ x2 |
− |
2 x |
|
)dx = |
|
|
|
|
|
|
|
||||||||||||
= 2(arctg x − |
x3 |
) |
1 |
|
= 2arctg1− |
1 |
= |
π |
− |
1 |
. |
|
|
|
|
|
|
|
|
||||||||
6 |
0 |
3 |
2 |
3 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
|
|
|
|
|
|
|
|

Объем тела вращения
Теорема 2.18. Пусть функция y = f (x) непрерывна на отрезке [a,b]. В этом случае объем тела, образованного вращением
около оси |
0x криволинейной трапеции, ограниченной графиком |
||
функции |
y = f (x) , прямыми |
x = a, x = b |
и осью абсцисс C |
(рис.5.5), может быть найден по формуле |
|
||
|
Vx =π∫b |
f 2 (x)dx |
(2.15) |
|
a |
|
|
Рис. 2.5 |
0у, то объем тела |
|
Если вращение происходит вокруг оси |
||
вращения находится по формуле |
|
|
Vy =π ∫2 |
φ2 (y)dy |
(2.16) |
c |
|
|
Рис. 5.6.
66
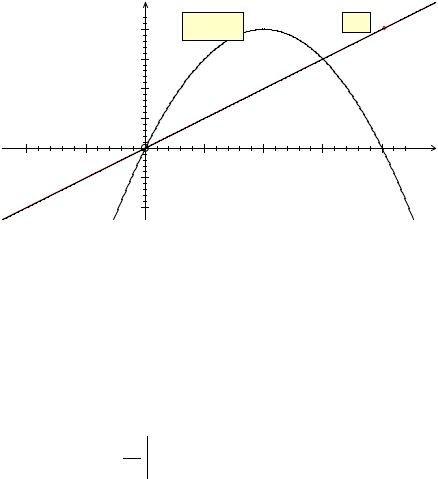
Пример 2.24. Вычислить объем тела, образованного вращением |
|||||||||||||||
фигуры, ограниченной линиями y = 4x − x2 |
и |
y = x вокруг оси 0x . |
|||||||||||||
Решение. Найдем точки пересечения |
линий |
y = 4x − x2 |
и |
||||||||||||
y = x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x − x2 = x, x2 −3x = 0, |
x(x −3) = 0, |
|
|
|
|
|
и |
||||||||
x1 = 0, |
y1 = 0 |
и |
x2 = 3, |
y2 = 3 (рис. 2.7) |
|
|
|
|
|
||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
y = 4x – x2 |
|
|
|
y = x |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
-1 |
|
|
1 |
2 |
|
3 |
|
|
4 |
x |
||
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.7. |
|
|
|
|
|
|
|
|
Объем вычислим как разность V1 −V2 объемов тел, |
получен- |
|
|||||||||||||
ных вращением околооси 0x фигуры, ограниченной линиями |
|
||||||||||||||
y = 4x − x2 , y = 0, |
x = 3 и фигуры, ограниченной линиями |
|
|||||||||||||
y = x, y = 0, x = 3. Тогда V =V1 −V2 =π∫3 |
(4x − x2 )2 dx − π ∫3 |
x2dx = |
|
||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
=π∫3 |
(16x2 −8x3 + x4 − x2 )dx = =π∫3 |
(15x2 −8x3 + x4 )dx = |
|
||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
15x3 |
|
8x4 |
x5 |
3 |
3 |
|
|
243 |
|
|
|
|
|
|
π ( |
|
3 |
− |
4 |
+ 5 ) |
0 =π (5 3 −2 81+ |
5 |
) = 21,6π |
|
|
|
|
|||
|
|
|
|
|
|
|
67 |
|
|
|
|
|
|
|
|
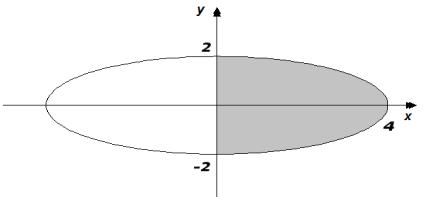
Пример 2.25. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями y2 = 4 − x, x = 0 вокруг оси
Oy .
Решение. Находим x = 4 − y2 при x = 0, y = ±2, при y = 0, x = 4 (рис. 2.8)
|
|
|
|
|
|
|
|
Рис. 2.8. |
|
|
|
|
|||
По формуле (2.16) имеем |
|
|
|
|
|
|
|
||||||||
Vy =π ∫2 |
x2dy = |
π ∫2 |
(4 − y2 )2 dy = 2π∫2 |
(16 −8y2 + y4 )dy = |
|||||||||||
−2 |
|
|
|
|
|
−2 |
|
|
|
|
0 |
|
|
|
|
2π (16y |
− |
8y3 |
+ |
y5 |
) |
|
2 |
= 2π (32 |
− |
64 |
+ |
32 |
) = |
512π |
|
|
|||||||||||||||
3 |
5 |
|
0 |
3 |
5 |
|
15 |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Длина дуги плоской кривой
Определение 2.7. Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, при условии, что количество звеньев ломаной линии неограниченно возрастает, и при этом длина наибольшего звена ломаной стремится к нулю (рис.5.9)
68

Рис. 5.9
Теорема 2.19. Если дуга задана непрерывно дифференцируемой функцией y = f (x) , то ее длина l вычисляется по формуле :
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
′ |
2 |
dx |
(2.17) |
|||
|
|
|
= ∫ 1+( f (x)) |
|
|||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
Пример 2.26. Вычислить длину линии |
y = lncos x от x = 0 до |
||||||||||||||
x = a, 0 < a < |
π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
Решение. Находим y′ = (ln(cos x))′ |
|
(−sin x). |
|||||||||||||
= |
|
||||||||||||||
cos x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
′ |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||
Тогда |
1+(y ) |
|
= |
1+ tg |
|
x = |
|
и |
по формуле (2.17) за- |
||||||
|
|
cos x |
|||||||||||||
ключаем, что
l = ∫a |
1 |
dx = ∫a |
|
cos x |
|||
0 |
0 |
=1 ln sin a +1 .
2 sin a −1
|
d(sin x) |
a |
d(sin x) |
|
1 |
|
sin x −1 |
|
a |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||
|
= ∫0 |
|
|
= − |
2 ln |
|
sin x +1 |
|
0 |
= |
|
|
1−sin2 x |
sin2 x −1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
69
2.3.8. Приложения определенного интеграла в экономике Расчет объема продукции. Если в некоторой идеализирован-
ной модели, |
где время t меняется непрерывно, задана непрерыв- |
|||||||||||||||||
ная функция |
p = f (t) , являющаяся производительностью труда в |
|||||||||||||||||
момент времени t , t [t0 ,t1 ], |
то объем продукции, |
произведенной |
||||||||||||||||
за промежуток времени ∆t = t1 −t0 |
|
вычисляется с помощью опре- |
||||||||||||||||
деленного интеграла |
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
V = ∫ p(t)dt |
|
|
|
|
|
|
|
|
(2.18) |
||||
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
Функция p(t) обычно подбирается эмпирическим путем. |
||||||||||||||||||
Расчет средних значений. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Определение 2.8. Число |
1 |
|
∫b |
f (x)dx |
называется средним |
|||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
b −a a |
|
|
|
|
|
|
|
|
|
||
значением непрерывной функции |
f (x) на отрезке [a,b]. |
|
||||||||||||||||
Напомним, что по теореме о среднем в определенном интегра- |
||||||||||||||||||
ле существует число c [a,b] |
, такое, что |
f (c) = |
|
1 |
|
∫b |
f (x)dx . |
|||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b −a a |
|
||||
Пример 2.27. Считая, что функция Кобба-Дугласа имеет вид |
||||||||||||||||||
p(t) = (1+t)e3t , |
вычислить объем продукции, |
произведенной за 4 |
||||||||||||||||
года. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
V = ∫4 |
(1+t)e3t dt = [u =1+t, |
du = dt, |
|
dv = e3t dt, |
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = 1 e3t |
]= (t +1) |
1 e3t |
|
0 4 − |
4 1 e3t dt = 1 (5e12 |
−1) − |
1 e3t |
|
0 4 = |
|||||||||
|
|
|||||||||||||||||
3 |
|
|
3 |
|
|
∫0 3 |
|
|
3 |
|
|
|
9 |
|
|
|
|
|
= 19 (14e12 −2) ≈ 2,53 105 (у.е)
70
