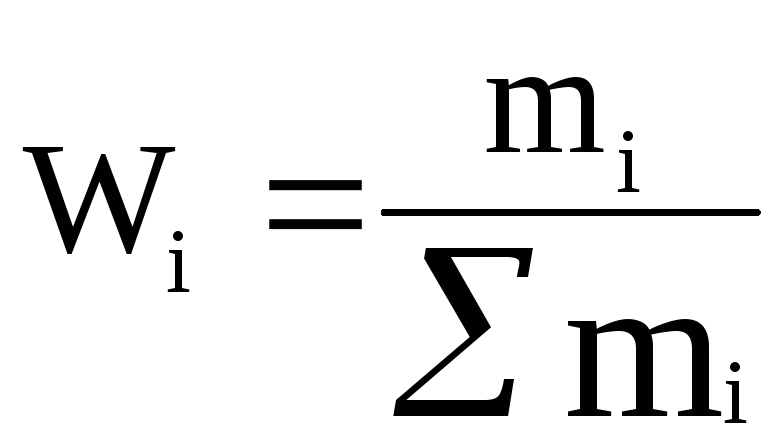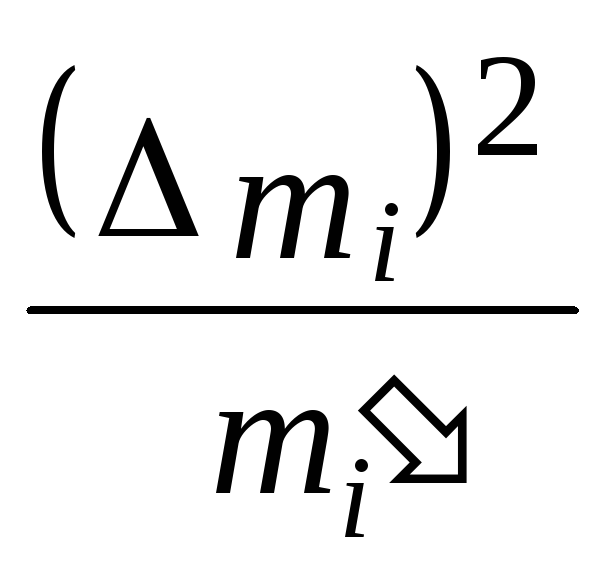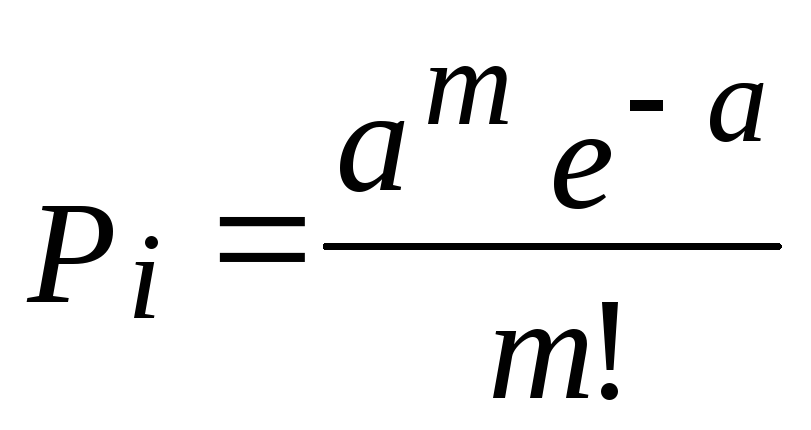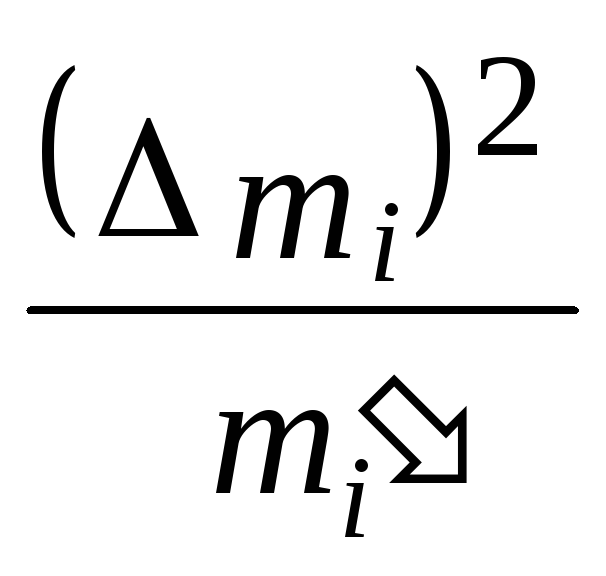3. Задание к лабораторной работе

Проверить согласованность случайной величины Х с биноминальным распределением и согласованность величины У с пуассоновским распределением. Для этого:

1. Определить наблюдаемые частоты по формуле:

2. Определить среднее значение величины по формуле:

3. Математическое ожидание случайной величины M(x) принять равным её среднему значению х_{ср :}

M(x) = х_ср

4. Найти вероятность наступления события во всех испытаниях по формуле:

5. Найти вероятность противоположного события по формуле:

q = 1 - p

6. Определить теоретическое значение вероятности по формуле

для биноминального распределения. Определить теоретическое значение вероятности по формуле

для пуассоновского распределения

7. Найти теоретические значения возможных значений дискретной случайной величины по формуле:

8. Вычислить значение критерия = Q по формуле

= Q =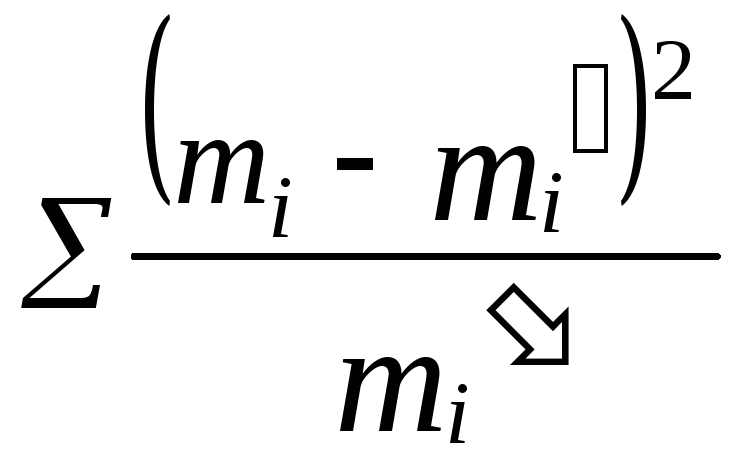

9. Число степеней свободы определить по формуле:

r = n – s -1

10. Для числа степеней свободы к и уровня значимости α по таблице “ Критические точки распределения ” найти критическую точкуи сделать вывод о согласованности случайной величины с предполагаемым распределением.

11. Сравнить значения и и сделать вывод о согласованности случайной величины с предполагаемым распределением.

12. Результаты вычислений занести в таблицу.

4. Контрольные вопросы.

1. Какое распределение дискретной случайной величины называется биноминальным?

2. Как определить вероятности возможных значений дискретной случайной величины в случае биноминального распределения?

3. При каких значениях n и р целесообразно использовать формулу Бернулли?

4. Какое распределение дискретной случайной величины называется распределением Пуассона?

5. Как определить вероятность возможных значений дискретной случайной величины в случае распределения Пуассона?

6. При каких значениях x, n и р целесообразно использовать формулу Пуассона?

7. Как определить параметр в случае распределения Пуассона?

8. Дать определения выборочной и генеральной совокупностей.

9. Что называется уровнем значимости?

10. Что называется критерием согласия χ² Пирсона ?

11. Что называется числом степеней свободы?

12. Сформулировать правило применения критерия Пирсона.

5. Образец решения задачи № 12

Задание 1

Биномиальное распределение

Пусть х– количество снятий автобусов с рейса а АТП – 10061 в течение месяца. Проверить гипотезу о биномиальном распределении случайной величиных по данным 1-го автоотряда.

хі	0	1	2	3	4	5
mі	53	32	18	6	3	1

Решение

Случайная величина хможет принимать следующие значения: х {0, 1, 2, 3, 4, 5}

Число сравниваемых значений: N= 6

Определим среднее значение величины по формуле:

Неизвестный параметр p биномиального распределения можно оценить по результатам измерений с помощью формулы:

Тогда q= 1 –p

q= 1 – 0,152 = 0,848

Пользуясь формулой биномиального распределения

Вычислим теоретические вероятности:

∑ Р = 1,00000

Сравнивая соответствующие значения

и

Наблюдаем определенную согласованность эмпирических и теоретических результатов.

Проверим согласованность эмпирических и теоретических значений и

Ожидаемое количество определим по формулездесьN= ∑m_i = 113

∑ = 113

Сравнивая эмпирические значения и соответствующие им теоретические значениянаблюдаем некоторую согласованность результатов. Проверим эту согласованность с помощью критерия Пирсона . Величину найдем по формуле:

Вычислим :

Вычислим :

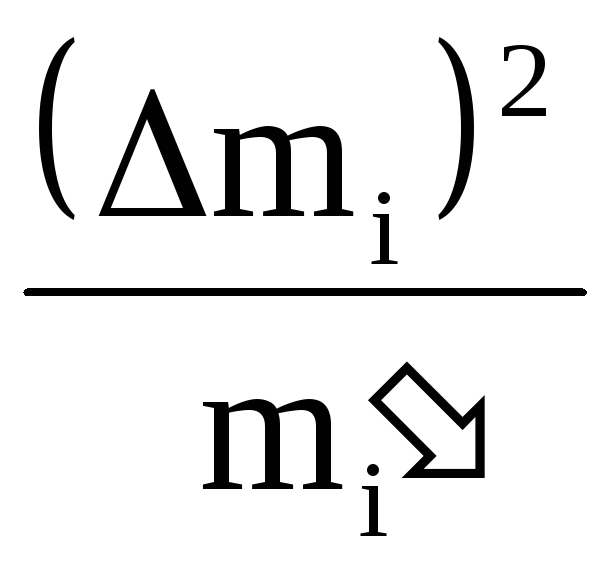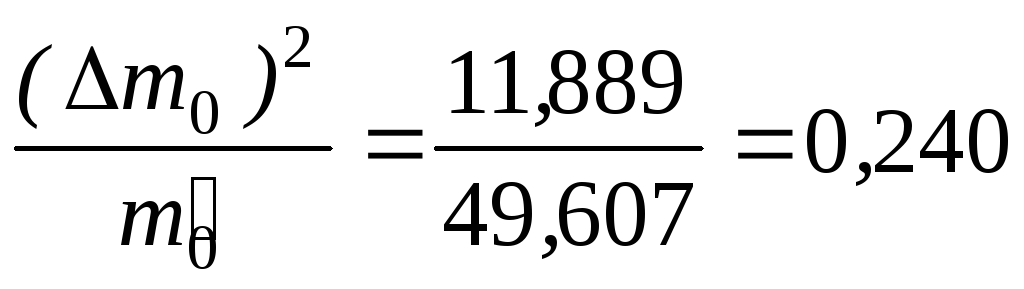
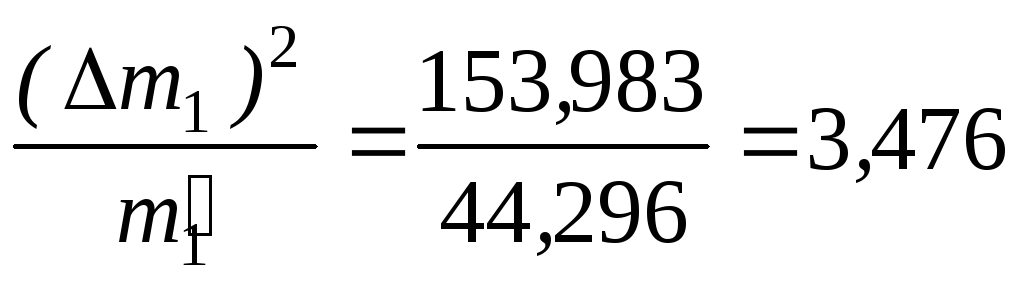
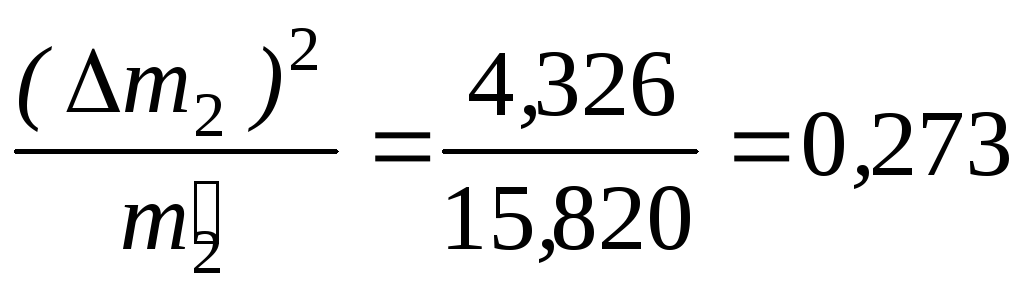
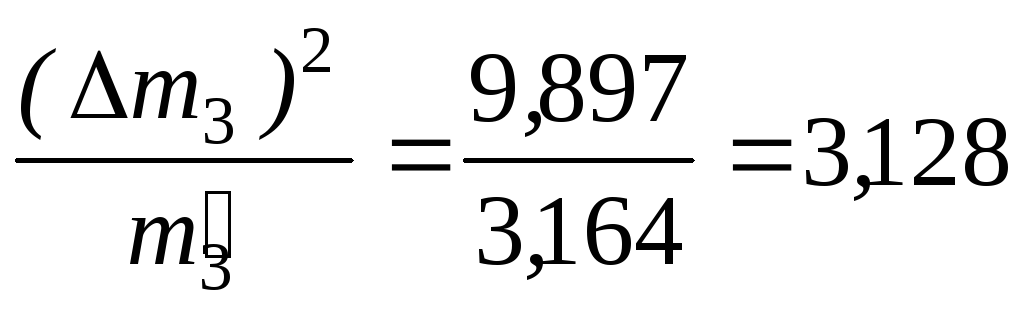
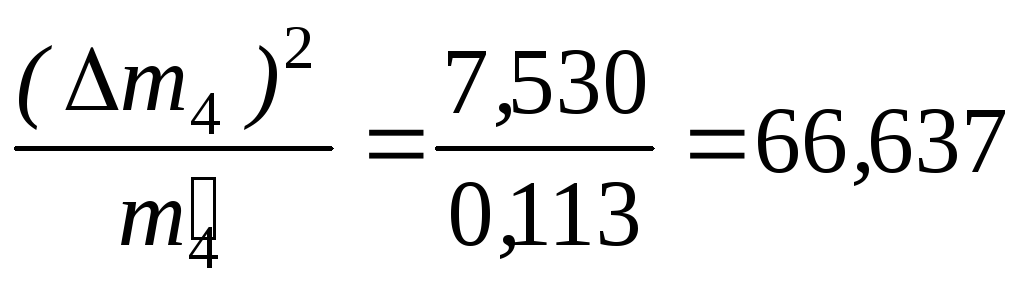
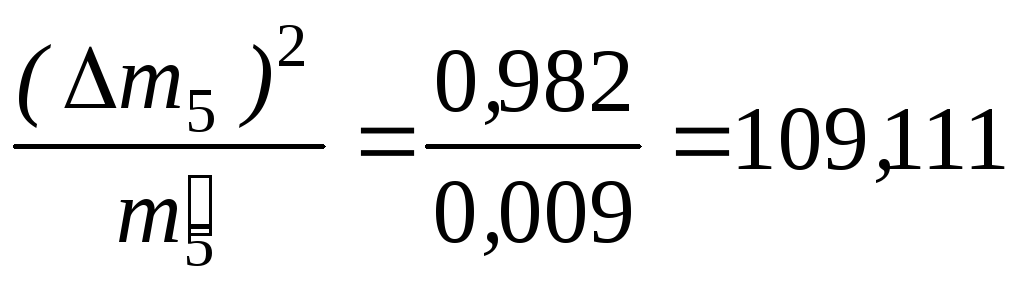
Меру расхождения Qопределим по формуле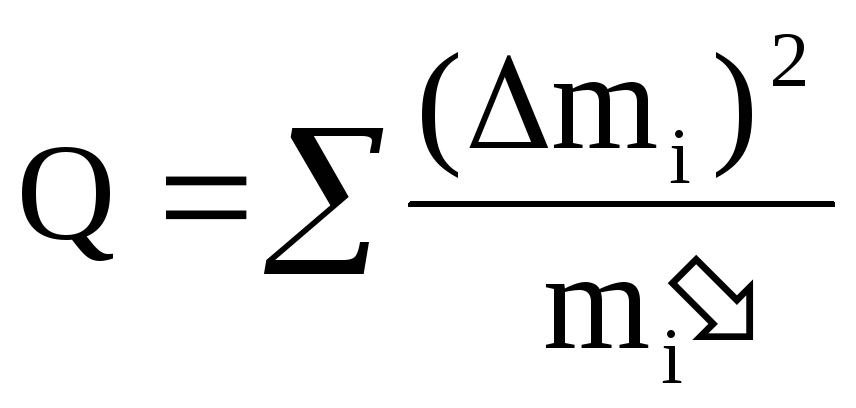

Q= 0,240 + 3,476 + 0,273 + 3,128 + 66,637 + 109,111 = 182,865

Q= 182,9

Число степеней свободы определим по формуле: r=n–s– 1

Здесь n= 6 – число значений, принимаемых величиной х.

S= 2 – число сравниваемых параметров

Имеем: r= 6 – 2 – 1 = 3

По таблице "Критические точки распределения" для числа степеней свободыr= 3 с уровнем значимости α = 0,01 определим:

= 11,3

Поскольку 182,9 › 11,3

Q›

Мера расхождения Qпревышает значение для числа степеней свободыr= 3 и уровня значимости α = 0,01. Следовательно, нет оснований считать дискретную случайную величинуХ биномиально распределенной.

Вывод: гипотеза о биномиальном распределении дискретной случайной величины

Х – количество снятий автобусов с рейса – отвергается.

Таблица № 1. Биномиальное распределение (задача № 12).

Возможные значения хi	0	1	2	3	4	5
mi	53	32	18	6	3	1
	0,469	0,283	0,159	0,053	0,027	0,009
	0,43851	0,39301	0,14088	0,02525	0,00226	0,00008
	49,552	44,409	15,920	2,854	0,256	0,009
	3,448	12,409	2,080	3,146	2,744	0,991
	11,889	153,983	4,326	9,897	7,530	0,982
	0,240	3,476	0,273	3,128	66,637	109,111

6. Образец решения задачи № 12

Задание ІІ

Распределение Пуассона.

Проверить гипотезу о распределении бактерий в чашке Петри по закону Пуассона по следующим данным.

хі	0	1	2	3	4	5	6	7
mі	8	16	18	15	9	7	0	0

Решение

В данном случае случайная величина х принимает значения

х Є { 0, 1, 2, 3, 4, 5, 6, 7 }

N= 8

Среднее значение случайной величины х определим по формуле:

∑m_i = 73

Параметр а пуассоновского распределения можно оценить по среднему значению

а =

а= 2,301

Закон распределения Пуассона

Вычислим значение .

Используем разложение функций в ряд Маклорена:

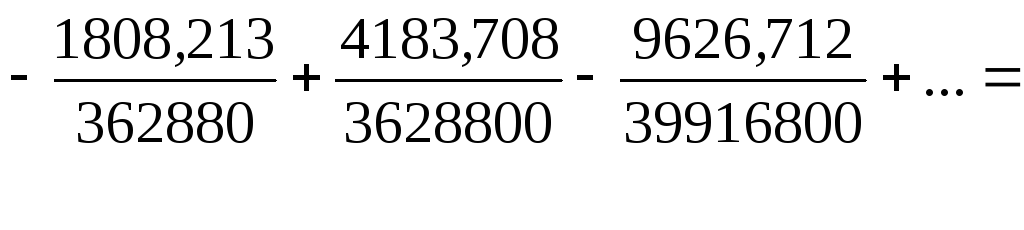
= 1 - 2,301 + 2,648 - 2,031 + 1,168 - 0,538 + 0,206 - 0,068 + 0,019 - 0,005 + 0,001 -0,0002+…

Вычисления производим с точностью α = 0,001. Поэтому значением функции с заданной точностью считаемS₁₁. При этом погрешность не превышает 0,0002.

= 0,099.

Вычислим теоретические значения вероятностей Р_і пуассоновского распределения.

Сравнивая соответствующие значения и наблюдаем определенную согласованность эмпирических и теоретических результатов.

Проверим согласованность эмпирических и теоретических значений m_i и.

Ожидаемое количество определим по формуле:

Сравнивая эмпирические значения m_iи соответствующие теоретические значениянаблюдаем согласованность результатов.

Проверим эту согласованность с помощью критерия Пирсона .

Величину найдем по формуле

Вычислим :

Вычислим

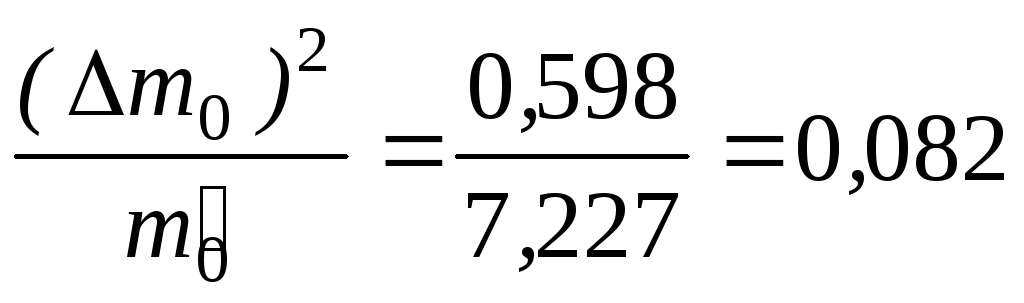
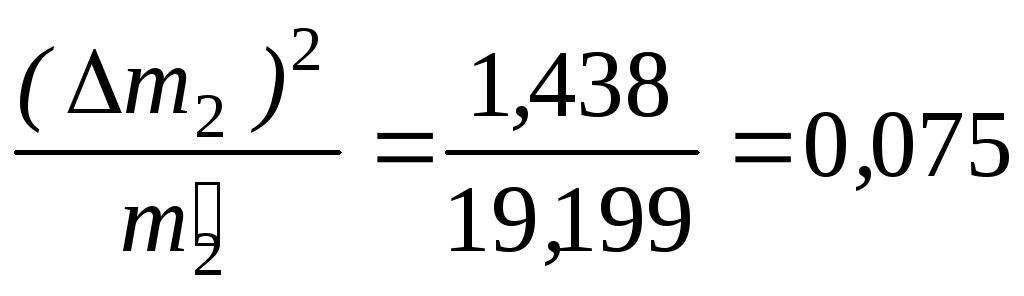
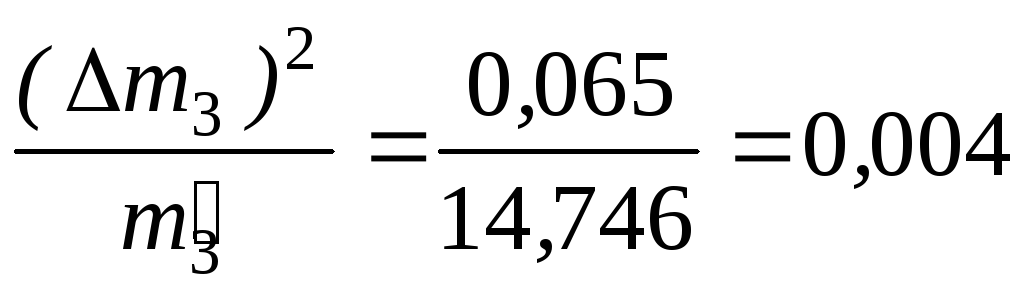
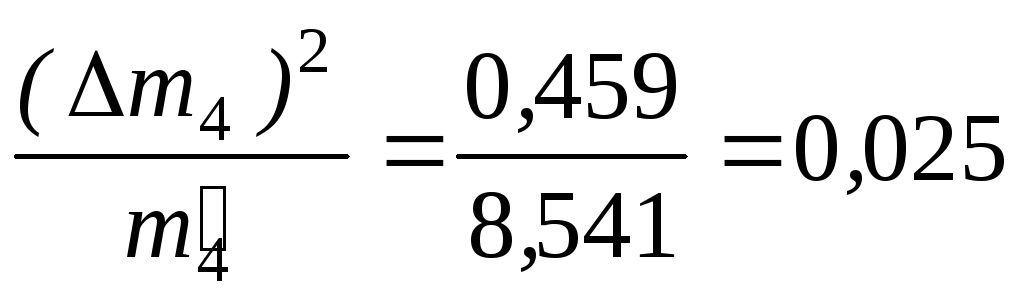
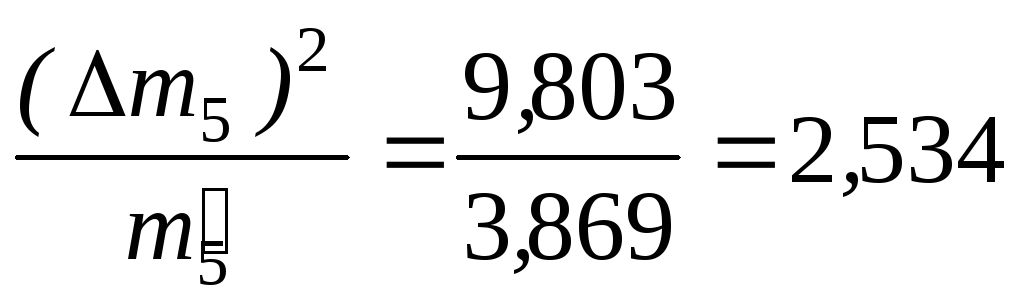
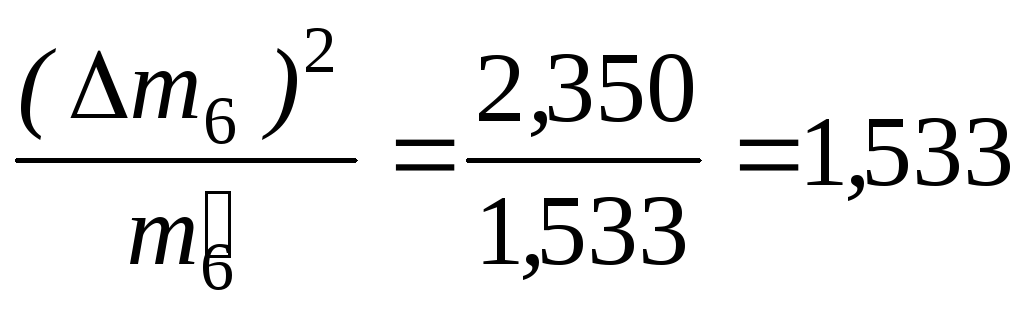
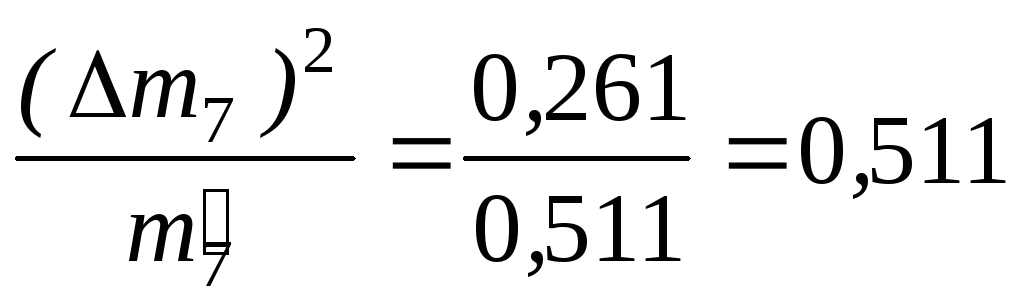
Меру расхождения Qопределим по формуле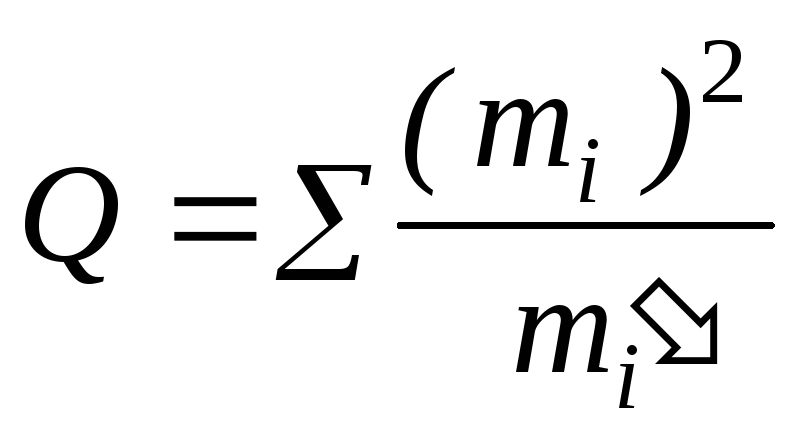

Q= 0,082 + 0,299 + 0,075 + 0,004 + 0,025 + 2,534 + 1,533 + 0,511 = 5,063

Q= 5,063

Число степеней свободы r определим по формуле: r=n–s– 1

Здесь n= 8 – число значений, принимаемых величиной Х.

S= 1 – число сравниваемых параметров.

Имеем: r= 8 – 1 – 1 = 6

По таблице "Критические точки распределения" для числа степеней свободыr= 6 с уровнем значимости α = 0,05 определим:

= 12,6

Поскольку 5,063 < 12,6

Q<

Мера расхождения Qне превышает значение для уровня значимости α = 0,05. Следовательно, есть основание считать дискретную случайную величинуХ распределенной по закону Пуассона.

Вывод: Случайную величину Хможно считать распределенной по закону Пуассона с параметрома= 2,301

Закон распределения

Гипотеза о пуассоновском распределении случайной величины хподтверждается.

Возможные значения хi	0	1	2	3	4	5	6	7
mi	8	16	18	15	9	7	0	0
wi =	0,110	0,219	0,247	0,205	0,123	0,096	0	0
	0,099	0,229	0,263	0,202	0,117	0,053	0,021	0,007
	7,227	16,717	19,199	14,746	8,541	3,869	1,533	0,511
	0,773	0,717	1,199	0,254	0,459	3,131	1,533	0,511
	0,598	0,514	1,438	0,065	0,211	9,803	2,350	0,261
	0,082	0,299	0,075	0,004	0,025	2,534	1,533	0,511