12

26.Интегрирование рациональных функций, некоторых иррациональностей и тригонометрических выражений.

1.Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение

2.Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;

3.Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

4.Вычислить интегралы от простейших дробей.

Шаг 1. Преобразование неправильной рациональной дроби

Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочленP(x) на Q(x). Получим следующее выражение:

где - правильная рациональная дробь.

Шаг 2. Разложение знаменателя на простейшие дроби

Запишем многочлен знаменателя Q(x) в виде

где квадратичные функции являются несократимыми, то есть не имеющими действительных корней.

Шаг 3. Разложение рациональной дроби на сумму простейших дробей.

Запишем рациональную функцию в следующем виде:

Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x).

Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.

Для интегрирования рациональных функций вида R(sin x,cos x) применяют подстановку t=tgx2, которая называется универсальной тригонометрической подстановкой. Тогда x=2arctg t, dx=2dt1+t2, sin x=2t1+t2, cos x=1−t21+t2. К

сожалению, универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками. Если R(−sin x,cos x)= =−R(sin x,cos x), то

делают заменуcos x=t и тогда sin xdx=−dt. При R(sin x,−cos x)=−R(sin x,cos x),

полагают sin x=t, при этом cos xdx=dt, а в случаеR(−sin x,−cos x)= =R(sin x,cos x) делают замену tg x=t, при которой  x=arctg t, dx=dt1+t2,sin x=t1+t2,cos x=11+t2, или ctg x=t.

. Основной приѐм решения иррациональных интегралов – это замена

переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции Последовательность

(1)Проводим подстановку после замены .

(2)Выносим константу за пределы интеграла. Числитель и знаменатель сокращаем на .

(3)Получившийся интеграл является табличным, готовим его для интегрирования, выделяя квадрат

(4)Интегрируем по таблице,

27.Понятие определенного интеграла и его свойства. Интегрирование кусочно-непрерывных функций. Замена переменной и интегрирование по частям. Формула Ньютона-Лейбница.

Основные свойства определенного интеграла

1. Будем считать, что определенный интеграл с одинаковыми пределами интегрирования равен нулю (по определению):

a

f ( x)dx 0.

a

2. Будем считать, что при перемене мест верхнего и нижнего пределов интегрирования определенный интеграл меняет знак на противоположный:

a b

f (x)dx f (x)dx .

b a

3.Пусть функции f (x) и g (x) интегрируемы на сегменте [a,b], тогда

5.Если функция f (x) интегрируема на сегменте [a,b] , то эта функция

интегрируема на любом сегменте [c, d ], содержащемся в сегменте [a,b] .

Основные правила интегрирования

Теорема: Любая непрерывная на интервале (a,b) функция f (x) имеет на

этом интервале первообразную. Одной из первообразных является функция:

x

F (x) f (t)dt ,

c

x

(x) f (t)dt C

f (t)dt (b) (a) ,

a

которое называется основной формулой интегрального исчисления или

формулой Ньютона – Лейбница.

Пусть выполнены следующие условия:

1)Функция f (x) непрерывна на отрезке [a,b] ;

2)отрезок [a,b] является множеством значений некоторой функции x g(t) ,

Указанная формула называется формулой замены переменной в

определенном интеграле.

Пусть функции u(x) и v(x) имеют непрерывные производные на сегменте [a,b] .

Тогда имеет место следующая формула интегрирования по частям для определенных интегралов:

Так как v (x)dx dv(x)и u (x)dx du(x) , то эту формулу можно записать следующим образом:

28.Геометрические приложения определенного интеграла. Физические приложения.

1. Площадь криволинейной трапеции, ограниченной кривой y =f(x)( f(x)>0), прямыми x = a , x = b и отрезком [ a , b ] оси Ох, вычисляется по формуле

2.Площадь фигуры, ограниченной кривыми y = f ( x ) и y = g ( x ) ( f ( x )< g ( x )) и прямыми х= a , x = b , находится по формуле

3.Если кривая задана параметрическими уравнениями x = x ( t ), y = y ( t ), то площадь криволинейной трапеции, ограниченной этой кривой и прямыми х=a , x= b , находится по формуле

4.Пусть S ( x )- площадь сечения тела плоскостью, перпендикулярной оси Ох, тогда объем части тела, заключенной между перпендикулярными оси плоскостями х=а и х= b , находится по формуле

5.Пусть криволинейная трапеция, ограниченная кривой y = f ( x ) и прямыми y=0, х=а и х= b , вращается вокруг оси Ох, тогда объем тела вращения вычисляется по формуле

6.Пусть криволинейная трапеция, ограниченная кривой х= g ( y ) и

прямыми x =0, y = c и y = d , вращается вокруг оси О y , тогда объем тела вращения вычисляется по формуле

7. Если плоская кривая отнесена к прямоугольной системе координат и задана уравнением y = f ( x ) (или x = F ( y )), то длина дуги определяется формулой

29.Приближенное вычисление определенных интегралов. Несобственные интегралы.

Приближенное вычисление определенных интегралов

Рассмотрим формулы приближенного вычисления:

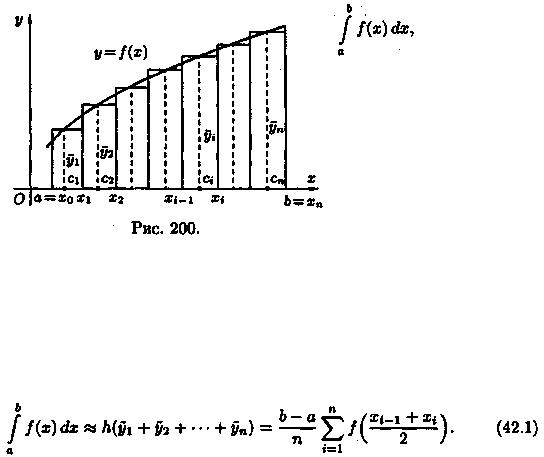
1) Формула прямоугольников

Пусть на отрезке [а; b], а < b, задана непрерывная функция ƒ(х). Требуется вычислить интегралчисленно равный площади соответствующей криволинейной

трапеции. Разобьем основание этой трапеции, т. е. отрезок [а; b], на n равных частей (отрезков)

длины 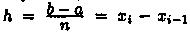с помощью точек х0= а, x1, х2,..., хn = b. Можно записать, что хi= х0+h• i, где i =

1,2,..., n

В середине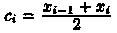каждого такого отрезка построим

ординату ŷi =ƒ(сi) графика функции у = ƒ(х). Приняв эту ординату за высоту, построим прямоугольник с площадью h • ŷi.

Тогда сумма площадей всех n прямо угольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла

2) Формула трапеций

Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Разобьем отрезок [а; b] на n равных частей длины Абсциссы точек деления а = х0, x1,х2,...,b = хn (рис. 201). Пусть у0,у1...,уn —

соответствующие им ординаты графика функции. Тогда расчетные формулы 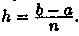для этих значений примут вид хi = a+h*i, уi=ƒ(xi), i= 0,1,2,..., n;

Заменим кривую у=ƒ(х) ломаной линией, звенья которой соединяют концы ординат yi и yi+1 (i = 0,1,2,.. .,n). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями уi, yi+1и

высотой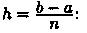

или

3) ормула парабол

Если заменить график функции у=ƒ(х) на каждом отрезке [xi-1;xi] разбиения не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла

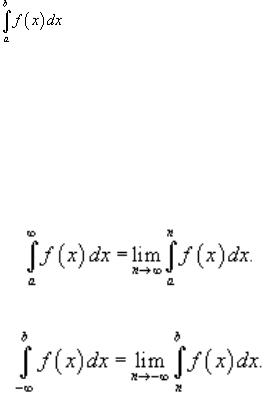
Суть этих методов – в замене подынтегральной функции интерполяционным многочленом. При этом возникает альтернативный выбор: осуществить замену подынтегральной функции одним интерполяционным многочленом высокой степени, описывающим изменение функции на всем интервале интегрирования

[a,b].

Несобственные интегралы

Определенный интеграл называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:

Предел a или b (или оба предела) являются бесконечными;

Функция f (x) имеет одну или несколько точек разрыва внутри интервала [a,b].

Бесконечные пределы интегрирования

Пусть f (x) является непрерывной функцией в интервале [a, ∞). Несобственный интеграл определяется через предел следующим образом:

Рассмотрим также случай, когда функция f (x) непрерывна в интервале (−∞, b]. В этом случае несобственный интеграл определяется как

Если указанные выше пределы существуют и конечны, то говорят что несобственные интегралы сходятся.

В противном случае интегралы расходятся.