
12
.pdfтакже справедливо для любого конечного числа функций, в частности, справедлива формула lim f n (x) lim f (x) n ;
|
|
Если существуют lim f (x) и lim g(x) 0 при каком-то условии, то |
||||||||
|
f (x) |
|
lim f (x) |
(при том же условии); |
||||||
lim |
|
|
|
|
|
|||||
|
|
|
|
lim g(x) |
|
|
|
|
||
g(x) |
|
|
|
|
|
|||||
|
|
Если |
f (x) g(x) h(x) и существуют lim f (x), |
|||||||
lim g(x) и |
lim h(x) |
, то |
lim f (x) |
. |
||||||
|
|
|
|
|
|
lim g(x) lim h(x) |
||||
Монотонная |
|
последовательность — |
это последовательность, элементы |
|||||||
которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.
Под числом e понимают предел
|
|
|
1 n |
|
|
lim |
1 |
|
|
|
|
|
|
||||
n |
|
|
n |
, |
|
|
|
|
|
||
|
|
|
|
|
|
который невозможно указать точным числом, но всегда можно
определить приближенно с учетом требуемой точности с помощью формулы
e 1 |
|
1 |
|
|
1 |
|
|
1 |
|
... |
1 |
|
|
|
|
|
1! |
2! |
3! |
n! |
n!n , |
||||||||||||
|
|
|
|
|
||||||||||||
где θ - это отношение разности
17.Предел функции. Понятие непрерывности и свойства функций, непрерывных в точке. Точки разрыва. Замечательные пределы. Сравнение бесконечно малых.
Непрерывность функции
Рассмотрим функцию f , определенную на промежутке X . Пусть x0 X .
Функция f называется непрерывной в точке x0 , если
lim f x f x0
x x0
Функция y f (x) |
|
называется непрерывной слева (справа) в точке |
||||
lim f x f x |
0 |
|
lim |
f x f x |
|
. Естественно, при этом функция |
x x0 0 |
|
|
0 |
|
|
|
|
|
x x0 0 |
|
|
|
|
должна быть определена в некоторой окрестности слева (справа) то
x0 , если
y f (x)
точки x0 .
Непрерывность функции в точке x0 означает непрерывность этой функции в
указанной точке как слева, так и справа.
Функция y f (x) , определенная на интервале a,b называется непрерывной на
интервале a,b , если она непрерывна в каждой точке x0 этого интервала
x0 a,b .
Функция y f (x), определенная на отрезке a,b ( a b) называется непрерывной на отрезке a,b , если она непрерывна в каждой точке x0 интервала a,b ,
непрерывна справа в точке b и непрерывна слева в точке a .
Общие свойства непрерывных функций, заданных на отрезке a,b , определяются четырьмя теоремами
Теорема. Пусть функция |
y f (x) определена и непрерывна на отрезке |
||
a,b , и на концах этого промежутка принимает значения разных знаков; |
|||
тогда найдется точка c (a,b), в которой функция равна нулю. |
|
||
Теорема Пусть функция |
y f (x) определена и непрерывна на отрезке |
||
a,b . Тогда, если |
f (a) f (b) то функция принимает все |
свои |
|
промежуточные значения, принадлежащие промежутку m, M , |
где |
||
m min f (a), f (b), |
M max f (a), f (b) , |
т.е. |
|
C (m, M ), (a,b) : f ( ) C.
Теорема . Пусть функция y f (x) определена и непрерывна на отрезкеa,b , тогда функция y f (x) является ограниченной на этом отрезке. Теорема Пусть функция y f (x) определена и непрерывна на отрезкеa,b , тогда функция y f (x) имеет минимум и максимум на этом отрезке
(множество значений функции включает в себя точные верхнюю и нижнюю границы).
Точки разрыва |
|
Непрерывность функции f в точке |
x0 , т.е. выполнение условия (3), означает, |
что оба односторонних предела f x0 |
0 и f x0 0 существуют и равны f x0 , |
т.е.
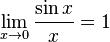
f x |
0 |
f x f x |
. |
|
0 |
|
|||
Условия.: |
|
|
|
|
|
1. |
f x0 0 и |
f x0 |
0 существуют; |
2.f x0 0 и f x0 0 конечны;
3. f x0 0 f x0 0 ;
4.f x0 0 f x0 0 f x0 .
Если 1. не выполнено, то |
называют точкой неопределенности. |
|||||||||
|
|
|
|
x0 |
|
|
|
|
|
|
Если 1. выполнено, а 2. |
не выполнено, то x0 называют точкой бесконечного |
|||||||||
скачка. |
|
|
|
|
|
|
|
|
|
|
Если выполнены 1. и 2., |
а 3. не выполнено, то |
x0 |
называют точкой конечного |
|||||||
|
|
|
|
|
|
|
|
|
|
|
скачка. Величина f (x0 |
0) f (x0 0) называется скачком функции f (x) в точке x0 |
|||||||||
. |
|
|
|
|
|
|
|
|
|
|
Если 1., 2., 3. выполнены, а 4. не выполнено, то |
x0 |
называют точкой |
||||||||
устранимого разрыва. |
|
|
|
|
|
|
|
|||
Если функция |
f определена в окрестности точки |
x0 и не определена в самой |
||||||||
точке x0 , то x0 |
также называют точкой разрыва. Такие точки классифицируют по |
|||||||||
той же схеме. |
|
|
|
|
|
|
|
|
|
|
Сравнение бесконечно малых величин: |
|
|
|
|
||||||
|
Две бесконечно малые величины и |
называются бесконечно |
||||||||
малыми одного порядка, если предел их отношения есть конечное число, |
||||||||||
отличное от нуля, т.е. |
lim |
|
k |
(k 0) ; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Величина |
|
называется бесконечно |
малой |
величиной высшего |
|||||
порядка по сравнению с |
, если предел отношения |
к |
равен нулю, т.е. |
|||||||
lim |
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина |
|
называется бесконечно |
малой |
величиной низшего |
|||||
порядка по сравнению с |
, |
если предел отношения к |
является бесконечно |
|||||||
большой величиной, т.е. lim |
|
; |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Две бесконечно малые величины и |
называются эквивалентными бесконечно малыми, |
|||||||||
если предел их отношения равен единице, т.е. |
|
|
|
|
||||||
Замечательные пределы:
Замечательный тригономерический предел
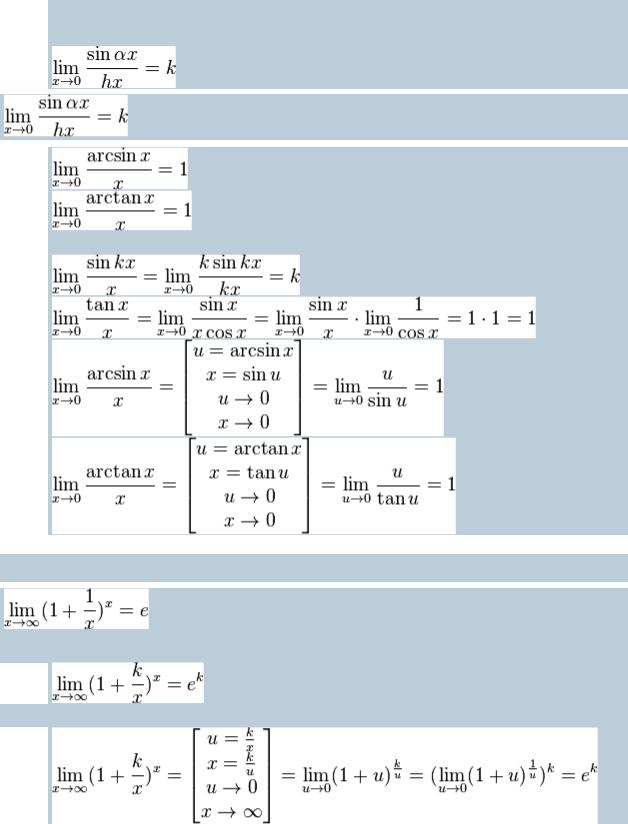
Следствие
: 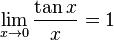
Доказательство
Замечательный показателе-степенной
следствие
доказательство

18.Функции, непрерывные на отрезке, и их свойства. Равномерная непрерывность.
. Функция f (x) называется равномерно-непрерывной на данном множестве, если для всякого ε > 0 можно найти такое δ = δ(ε) > 0, что |f (x1) — f (x2)|<ε для любой пары чисел x1 и x2 из данного множества, удовлетворяющей условию |x1—x2|< δ Например,
функция f (x) = x2 равномерно непрерывна на отрезке [0, 1]: если 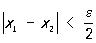 x1 ≤ 1, 0 ≤ x2 ≤ 1 обязательно |x1 + x2|≤ 2).
x1 ≤ 1, 0 ≤ x2 ≤ 1 обязательно |x1 + x2|≤ 2).
Так, например, функция 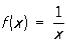 непрерывна в каждой точке интервала 0 < x < 1, но не является равномерно непрерывной в этом интервале, потому что, например, при ε = 1 для
непрерывна в каждой точке интервала 0 < x < 1, но не является равномерно непрерывной в этом интервале, потому что, например, при ε = 1 для
любого δ > 0 (δ < 1) мы имеем удовлетворяющие неравенству |x1 — x2| < δ числа x1 = 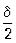 и x2= δ ,
и x2= δ ,
для которых 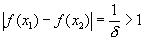
Функция |
называется непрерывной на отрезке |
, |
если она является |
|
непрерывной в |
интервале |
, непрерывной справа |
в точке , то |
|
есть |
и непрерывной слева в точке , то есть |
|
. |
|
|
|
|
|
|
Свойства функций непрерывных на отрезке:
1. . Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.
2. Непрерывная на отрезке 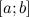 функция является ограниченной на этом отрезке. 3. . Если функция
функция является ограниченной на этом отрезке. 3. . Если функция 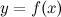 является непрерывной на отрезке
является непрерывной на отрезке 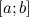 и принимает на
и принимает на
концах этого отрезка неравные между собой значения, то есть 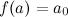 ,
, 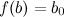
,то на этом отрезке функция принимает и все промежуточные значения между 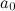
и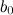 .
.
4.Если функция 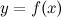 , которая непрерывна на некотором отрезке
, которая непрерывна на некотором отрезке 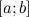 , принимает на концах отрезка значения разных знаков, то существует такая точка
, принимает на концах отрезка значения разных знаков, то существует такая точка 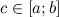 такая, что
такая, что 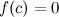 .
.
5.Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

19.Понятие производной, ее геометрический и физический смысл. Основные правила дифференцирования. Таблица производных. Определение и смысл производной
1) Физический смысл производной.
Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная – скорость изменения переменной y относительно переменной x в точке. Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная – скорость в момент времени. Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то – скорость изменения количества электричества в момент времени, т.е. сила тока в момент времени.
2) Геометрический смысл производной.
Пусть L – некоторая кривая,M0 – точка на кривой L.
Любая прямая, пересекающая L не менее чем в двух точках называется секущей. Касательной к кривой Lв точке M0 называется предельное положение секущей M0M1, если точка M1 стремится к M0, двигаясь по кривой.
Из определения очевидно, что если касательная к кривой в точке M0существует, то она единственная
Правила дифференцирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Будем считать, что функции |
u, |
v, |
w дифференцируемы, т.е. имеют |
|||||||||||||||
производные u , |
v , |
w . Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.Функция u v дифференцируема и u v u v ; |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cu ; |
2.Если c - постоянная, то функция cu дифференцируема и cu |
||||||||||||||||||
3.Из 1 и 2 следует, что c u c |
2 |
v c u |
c |
2 |
v ; |
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
4.Функция uv дифференцируема и uv |
u v uv |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.Из 4 следует, что uvw u vw |
uv w uvw ; |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
u v uv |
|
|
|
||||||
6.Если u определена и дифференцируема, то |
|
|
|
|
|
|
. |
|
||||||||||
|
|
v2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|||||
|
v |
|
|
|
|
|
|
|
|
|
|
|||||||

Таблица производных
Основные элементарные функции дифференцируемы всюду, где они определены. Производные этих функций могут быть вычислены по определению, т.е. по формуле:
f |
|
f x0 x f x0 |
|
||
x lim |
x |
|
|
x 0 |
и с помощью правил дифференцирования. Полученные значения производных основных элементарных функций приведем в таблице.
c 0;
x |
|
|
|
; |
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x |
|||||
|
|
|
|
|
2 |
|
||
(x ) x 1 ; |
|
|
|
|
|
|
|
||||||||||||||||||
(a |
x |
a |
x |
ln a ; |
|
|
|
|
|
|
|
||||||||||||||
|
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
(e |
x |
|
e |
x |
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(log a x) |
|
|
|
1 |
|
|
; |
|
|
|
|
||||||||||||||
|
|
x ln a |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(ln x) |
|
|
|
|
x |
||||||||||||||||||||
|
|
|
|
cos x ; |
|
|
|
|
|
|
|
||||||||||||||
(sin x) |
|
|
|
|
|
|
|
||||||||||||||||||
(cos x) |
|
|
|
sin x ; |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
cos2 x ; |
||||||||||||||||||||||
(tgx) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(ctgx) sin 2 x ; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(arctgx) |
|
1 x2 ; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
1 x2 ; |
|||||||||||||||||||||
(arcctgx) |
|
|
|||||||||||||||||||||||
(arcsin x) |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
x2 ; |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(arccos x) |
|
|
|
|
1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x2 . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||
20.Дифференциал и его применения. Производные и дифференциалы высших порядков.
Дифференциал первого порядка и его применение. Функция у = f(x) на-
зываетсядифференцируемой в точке х0, если ее приращение в этой точке может бытьпредставлено в виде
Ау = А-Ах + о(Ах). |
(1) |
Главнаяпри АФ О линейная часть ААх приращения Ау называется дифференциаломэтой функции в точке х0, соответствующим приращению Лх, и обозначается символом dy .
Для того, чтобы функция у = f(x) была дифференцируемой в точке х0, необходимо и достаточно, чтобы существовала производная f'(x0), при этом справедливо равенство А =f'(x0).
Это утверждение позволяет называть дифференцируемой всякую функцию, имеющую производную. Вводя обозначение dx = Ах, получаем формулу для вычисления дифференциала
dy = y'dx.
Для дифференциала установлено:
1)Дифференциал функции равен произведению ее производной на дифференциал аргумента (независимой переменной).
2)Разность между приращением функции ∆y и ее дифференциалом dy есть величина бесконечно малая более высокого порядка малости, чем приращение аргумента ∆x,1а также (при y/≠0) более высокого порядка, чем приращение функции ∆y и ее дифференциал dy.
3)Приращение функции ∆y и ее дифференциал dy при бесконечно малом ∆x являются равносильными бесконечно малыми dy≈∆y
Производные высших порядков
Если функция f (x), определенная в A , имеет производную во всех точках A, то эту производную можно рассматривать как новую функцию g(x) f '(x) ,
x A .
К этой функции применимы все предельные законы, в том числе и дифференцирование.
Если g(x) , определенная в A, имеет конечную производную g'(x) в точке
x A, то значение этой производной является второй производной функции
f (x).
Аналогично вычисляются производные более высоких порядков.


21.Свойства функций, дифференцируемых на отрезке.
Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке)..
Свойства дифференцируемых функций
ЕОРЕМА 1. Если функция 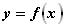 имеет производную на множестве X, то она непрерывна на этом множестве.
имеет производную на множестве X, то она непрерывна на этом множестве.
ДОКАЗАТЕЛЬСТВО.
Из условия теоремы следует, что отношение 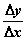 имеет конечный предел для любого X из множества X при
имеет конечный предел для любого X из множества X при 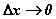 , то есть:
, то есть:
По теореме, определяющей необходимое и достаточное условие существования предела, будем иметь:
Где 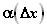 – бесконечно малая функция при
– бесконечно малая функция при 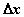 , стремящемся к нулю. Находим приращение функции:
, стремящемся к нулю. Находим приращение функции:
Оно складывается из двух бесконечно малых функций при 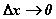 , поэтому их сумма
, поэтому их сумма  бесконечно мала, что и доказывает непрерывность функции
бесконечно мала, что и доказывает непрерывность функции  .
.
Дифференцируемая функция непрерывна, значит, она имеет и предел в соответствующих точках..
ТЕОРЕМА 2. Если 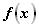 и
и  дифференцируемы на множестве X, то производная суммы (разности) функций равна сумме (разности) их производных
дифференцируемы на множестве X, то производная суммы (разности) функций равна сумме (разности) их производных
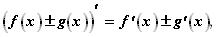 (11. 1)
(11. 1)
ТЕОРЕМА 3. Если для функции 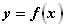 существует обратная функция
существует обратная функция 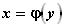 и в
и в
рассматриваемой точке Х производная  , то обратная функция в соответствующей точке дифференцируема, причем
, то обратная функция в соответствующей точке дифференцируема, причем
ДОКАЗАТЕЛЬСТВО.
Придадим значению у приращение 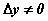 , тогда функция
, тогда функция 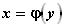 получит приращение
получит приращение 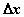 , которое также отлично от нуля. Действительно, если бы
, которое также отлично от нуля. Действительно, если бы 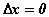 ,
,
то 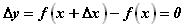 , что невозможно. Следовательно, можно записать:
, что невозможно. Следовательно, можно записать:
