12

11.Кривая на плоскости. Уравнения прямой на плоскости. Угол между прямыми. . Виды кривых второго порядка.

Кривые на плоскости:

Спирали плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от неѐ.

Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса r, катящейся без скольжения по прямой.

Астроида — плоская кривая, описываемая точкой M окружности радиуса r, катящейся по внутренней стороне окружности радиуса R = 4r

уравнение прямой на плоскости в прямоугольной системе координат Oxyесть некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой.

где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая

прямая на плоскости задается уравнением вида .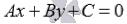

Угол между прямыми.

Угол ( между 2-мя параллельными прямыми равен 0, тогда tg(=0; с другой стороны, из условия параллельности, т.е. из равенства k1= k2, следует, что k1k2=0 и по формуле tg(=k2-k1/1+k1k2-угол между 2-мя пересекающимися прямыми-получаем: k1-k2/1+k1k2=0.

Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.

и алгоритм для нахождения расстояния от заданной точки 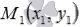до заданной прямой a:

находим общее уравнение прямой a вида 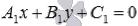или уравнение прямойa с угловым коэффициентом ;

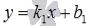получаем общее уравнение прямой b вида или уравнение прямой b с угловым коэффициентом вида 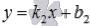, учитывая, что

прямая bпроходит через заданную точку M1 и перпендикулярна заданной прямой a;

определяем координаты 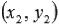точки H1 - точки пересечения прямых a и b,

вычисляем требуемое расстояние от точки M1 до прямой a по формуле .

Общее уравнение кривой второго порядка имеет вид:

a11x2 + 2a12xy + a22y2 + 2a1x +2a2y +a = 0

в котором хотя бы один из коэффициентов a11, a22, a12 отличен от нуля.

Имеются следующие виды кривых второго порядка: эллипс, парабола, гипербола (конические сечения), пара пересекающихся прямых, пара параллельных прямых, одна прямая, точка, пустое множество.

12.Кривые и поверхности в пространстве. Различные уравнения плоскости. Уравнение прямой в пространстве. Расстояние от точки до прямой или плоскости. Угол между плоскостями и прямыми.

1Поверхности вращения линейчатые.

Все поверхности этого класса образованы вращением прямой линии вокруг другой прямой. Две прямые могут занимать относительно друг друга три различных положения. Каждому из них соответствует своя поверхность вращения.

Конус образуют вращением прямой вокруг пересекающейся с ней оси

Для построения точки, принадлежащей кривой поверхности, еѐ поверхности располагаем на проекциях линии, лежащей на этой поверхности.

Цилиндр образуют вращением прямой вокруг параллельной ей оси

Однополостный гиперболоид образуют вращением прямой вокруг скрещивающейся с ней оси

2 Поверхности вращения нелинейчатые.

К этому классу относят в основном поверхности, образованные вращением кривых второго порядка.

Сферу образуют вращением окружности вокруг еѐ диаметра Любая плоскость пересекает сферу по окружности

Круговой тор образуют вращением окружности вокруг оси, лежащей в плоскости этой окружности и не являющейся еѐ диаметром.

Эллипсоид образуют вращением эллипса вокруг его малой или большой оси

Двуполостный гиперболоид образуют вращением гиперболы вокруг еѐ действительной оси

Если кривую линию без еѐ деформации нельзя совместить всеми точками с плоскостью, то еѐ называют пространственной. К таким кривым относят винтовые линии.

Винтовая линия – это траектория движения точки, равномерно перемещающейся вдоль образующей, которая равномерно вращается вокруг оси этой поверхности

Виды уравнений плоскости.

Существуют следующие виды ур-ий плоскости: 1) Общее ур-е плоскости:

Ax+By+Cz+D=0, где (n=(A,B,C)- нормальный вектор плоскости. 2) ур-е плоскости, проходящей через точку М1(x1;y1;z1) перпендикулярно вектору (n=(A,B,C): A(x-x1)+B(y- y1)+C(z-z1)=0. 3)Ур-е плоскости в отрезках:

x/a+y/b+z/c=1, где a,b,c-величины отрезков, отсекаемых плоскостью на осях координат. 4)Нормальное ур-е плоскости: x(Cos () +y(Cos ()+z(Cos ()+(=0,

где Cos (, Cos (, Cos (-направляющие Cos –сы нормального вектора; (-расстояние от начала координат до плоскости. Общее ур-е приводится к нормальному виду путѐм умножения на нормирующий множитель.

Уравнение прямой в пространстве

если две плоскости в пространстве имеют общую точку, то они имеют общую прямую, на которой находятся все общие точки этих плоскостей. Таким образом, прямую линию в пространстве можно задать, указав две плоскости, пересекающиеся по этой прямой.

Угол между двумя пересекающимися по прямой c плоскостями и 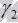– это угол между двумя пересекающимися прямыми a и b, по которым плоскост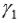и и 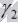пересекаются с плоскостью 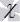, перпендикулярной к прямой c.

13.Квадратичные формы, приведение их к каноническому виду. Знакоопределенность форм. Критерий Сильвестра.

Квадратичной формой F(x1 , x2 , , xn ) от n неизвестных x1 , x2 , , xn называется сумма,

каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.

Канонический базис квадратичной формы

Принято считать, что квадратичная форма F(X ) имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. aij 0 при i j .

При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами aii , т.е.:

n

a11 x12 a22 x2 2 ann xn 2 aii xi 2.

i1

Вэтом случае матрица квадратичной формы имеет диагональный вид:

В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Теорема (Критерий Сильвестра). Справедливы следующие утверждения:

1. Квадратичная форма F( X ) X T AX положительно определена тогда и только тогда, когда главные миноры матрицы A положительны.

2.Квадратичная форма F( X ) X T AX отрицательно определена

тогда и только тогда, когда главные миноры матрицы A четного порядка положительны, а главные миноры матрицы A нечетного порядка отрицательны.

Доказательство: Докажем первое утверждение.

Аналогично доказывается второе утверждение теоремы.

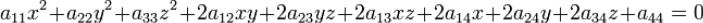
14.Поверхности второго порядка, их классификация.

в котором по крайней мере один из коэффициентов 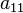, , 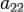, , 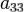, 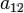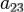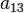отличен от нуля.

Классификация поверхностей второго порядка:

15)y 2 a 2 (a>0) две параллельные плоскости

16)y 2 a2 (a>0) две мнимые параллельные плоскости

17)y 2 0 две совпадающие плоскости

15.Элементы теории множеств и математической логики. Действительные числа. Грани. Понятие функции. Обратная функция.

Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:

N - множество натуральных чисел; Z - множество целых чисел;

Q– множество рациональных или дробных чисел;

R- множество действительных чисел.

Запись α¯¯ означает "не α", то есть отрицание утверждения α.

Запись α β означает "из утверждения α следует утверждение β". ( − символ импликации).

Запись α β означает "Утверждение α эквивалентно утверждению β", то есть из α следует β, а из β следует α (" − " символ эквивалентности).

Определение. Число m называется нижней гранью множества E, если оно является наибольшим из нижних границ множества E.

Обозначается нижняя грань: m=infE. Произносится inf, как инфимум

m=infE { x E(x≥m), ε>0 x′ E(x′<m+ϵ).

Определение. Число M называется верхней гранью множества E, если оно является наименьшим из верхних границ множества E.

Обозначается верхняя грань: M=supE. Произносится sup, как супремум

M=supE { x E(x≤M), ε>0 x′′ E(x′′>M−ϵ).

Некоторые свойства граней

1. Если множество A является подмножеством множества Bили совпадает с ним, то верхняя грань множества A меньше либо равна верхней грани множества B, а нижняя грань множества A больше либо равна нижней грани множества B.

A B supA≤supB, infA≥infB

2. Для любых множеств A и B супремум (верхняя грань) суммы A и B равен сумме супремумов этих множеств. Аналогично для инфимума (нижней грани): инфимум суммы множеств A и B равен сумме инфимумов этих множеств.

A,B: sup(A+B)=supA+supB, inf(A+B)=infA+infB. A+B={x+y,x A,y B}.

3. Для любых множеств A и B супремум (верхняя грань) произведения A и B равен произведению супремумов этих множеств. Аналогично для инфимума (нижней грани): инфимум произведения множеств A и B равен произведению инфимумов этих множеств.

A,B: sup(A B)=supA supB, inf(A B)=infA infB. A B={x y,x A,y B}.

4. Для любого множества A, являющегося подмножеством множества действительных чисел супремум −A равен минус инфимуму A, а инфимум −A равен минус супремуму A.

A R: sup(−A)=−infA, inf(−A)=−sup(A).

−A={−x,x A}.

Функция – это зависимость переменной y от переменной x. Это такая зависимость, при которой каждому значению переменной x соответствует только одно значение переменной y.