
12
.pdf
6.Произвольные системы линейных алгебраических уравнений. Теорема КронекераКапелли. Однородные системы. Фундаментальная система решений. Неоднородные системы.
Теорема Кронекера-Капелли
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.
Однородные системы уравнений
Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:
a11 x1 a12 x2 a1n xn 0 |
|||||||||
|
|
|
|
|
a2n xn 0 |
||||
a21 x1 a22 x2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x a |
m 2 |
x |
2 |
a |
mn |
x |
n |
0 |
|
m1 1 |
|
|
|
|
||||
Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.
Доказательство: Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что r не превосходит n . В случае r n система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при
r n.
Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа
неизвестных, всегда имеет ненулевое решение.
Доказательство: |
Если у системы уравнений m n, то ранг r |
системы не превышает числа |
||||||
уравнений m , т.е. |
r m. Таким образом, выполняется условие |
r n и, значит, система имеет |
||||||
ненулевое решение. |
|
|
|
|||||
Следствие 2: Однородная система n |
уравнений с n неизвестными имеет ненулевое решение |
|||||||
тогда и только тогда, когда ее определитель равен нулю. |
|
|
||||||
Доказательство: |
Допустим, система |
n линейных однородных |
уравнений, матрица |
которой |
||||
A [aij ]n n с определителем |
|
A |
|
, имеет ненулевое решение. Тогда по доказанной теореме |
r n, а |
|||
|
|
|||||||
это значит, что матрица A вырожденная, т.е. A 0 .

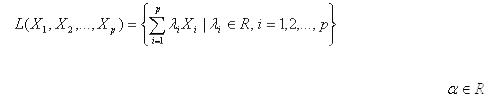
7.Линейные пространства. Подпространства. Базис, размерность. Линейная оболочка.
Линейное пространство 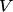 называется n-мерным, если в нем существует система из
называется n-мерным, если в нем существует система из 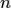 линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число
линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число 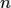 называется размерностью (числом измерений) линейного пространства
называется размерностью (числом измерений) линейного пространства 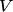 и обозначается
и обозначается  . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве
. Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве 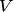 найдется система, состоящая из
найдется система, состоящая из 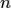 линейно независимых векторов, то такое пространство называют бесконечномерным (записывают:
линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: 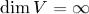 ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
Базисом n-мерного линейного пространства называется упорядоченная совокупность 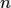 линейно независимых векторов (базисных векторов).
линейно независимых векторов (базисных векторов).
Теорема разложении вектора по базису. Если 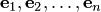 — базис n-мерного линейного пространства
— базис n-мерного линейного пространства  , то любой вектор
, то любой вектор 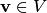 может быть представлен в виде линейной комбинации базисных векторов:
может быть представлен в виде линейной комбинации базисных векторов:
V=v1*e1+v2*e2+…+vn+en
и притом единственным образом, т.е. коэффициенты 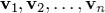 определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Действительно, размерность пространства 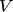 равна
равна 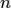 . Система векторов
. Система векторов 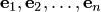 линейно независима (это базис). После присоединения к базису любого вектора
линейно независима (это базис). После присоединения к базису любого вектора  , получаем линейно
, получаем линейно
зависимую систему  (так как это система состоит из
(так как это система состоит из 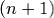 векторов n-мерного пространства).
векторов n-мерного пространства).
Пусть  – система векторов из
– система векторов из 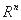 . Линейной
. Линейной
оболочкой 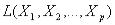 системы векторов
системы векторов 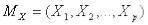 называется множество всех линейных комбинаций векторов данной системы, т.е
называется множество всех линейных комбинаций векторов данной системы, т.е
Свойства линейной оболочки: Если 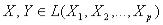 , то для
, то для 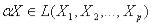 и
и 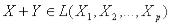 .
.
Линейная оболочка обладает свойством замкнутости по отношению к линейным операциям (операции сложения и умножения на число).
Если у нас есть некоторое линейное пространство 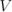 и векторы
и векторы 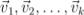 , по которым мы построили линейную оболочку
, по которым мы построили линейную оболочку 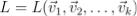 , то эта линейная оболочка тоже будет являться линейным пространством
, то эта линейная оболочка тоже будет являться линейным пространством

8.Евклидовы пространства. Норма вектора. Ортонормированный базис. Процесс ортогонализации. Неравенство Коши-Буняковского.
Вещественное линейное пространство L называется евклидовым, если в нѐм определена операция скалярного умножения: любым двум элементам x, yÎ L сопоставлено вещественное число a = (x, y) , удовлетворяющее следующим требованиям,
каковы бы ни были элементы x, y,zÎ L и число aÎR :
1.(x, y) = (y, x);
2.(x + y,z) = ((x,z) + (y,z));
3.(ax, y) = (x,ay) = a(x, y);
4.(x, x) > 0 для всех x ¹ q ;
5.(x, x) = 0 , если x = q .
Ортонормированный базис – это базис, состоящий из единичных (нормированных) и взаимно перпендикулярных (ортогональных) векторов. В этом случае базисные вектора имеют особые обозначения:
e1 = i, e2 = j, e3 = k.
(Неравенство Коши-Буняковского). Справедливо неравенство 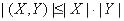 . Причем равенство достигается тогда и только тогда, когда
. Причем равенство достигается тогда и только тогда, когда 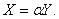 Доказательство: для любых
Доказательство: для любых 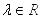 справедливо неравенство
справедливо неравенство
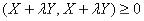 . (1)
. (1)
Причем равенство достигается лишь в том случае, когда 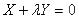 или
или 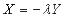 . Используя линейность и коммутативность скалярного произведения, неравенство (1) можно записать в виде
. Используя линейность и коммутативность скалярного произведения, неравенство (1) можно записать в виде
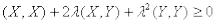 .
.
Разделив данное неравенство на положительное число 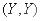 , получим
, получим
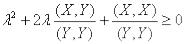 .
.
Это неравенство преобразуем к виду
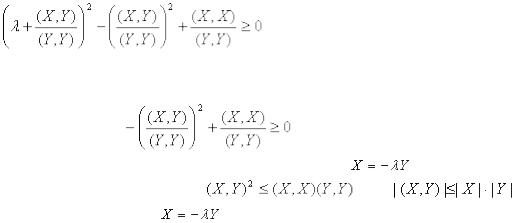
Поскольку неравенство справедливо для любых 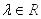 , то положив
, то положив 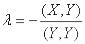 получим
получим
|
. (2) |
|
|
Отметим при этом, что равенство достигается при |
|
. Из неравенства (2) |
|
следует |
|
или |
. Причем равенство |
достигается лишь при |
. |
|
|

9.Линейные операторы. Их свойства и действия над ними. Обратный оператор. Преобразование матрицы линейного оператора. Подобные матрицы.
Справедливы следующие свойства линейных операторов из L(V, V):
1°. λ(АВ)=(λА)В; 2°.(А+В)С=АС+ВС; 3°.А(В+С)=АВ+АС; 4°.(АВ)С=А(ВС).
Первое из свойств следует из определения произведения линейного оператора на скаляр и определения произведения операторов Перейдем к обоснованию свойства 2°.

((А + В)С)х = (А + В)(Сх) = А(Сх) + В(Сх) = (АС)х + (ВС)х = (АС + ВС)х.
Сравнивая левую и правую части последних соотношений, мы получаем равенство (А + В)С = АС + ВС. Свойство 2° установлено.
Совершенно аналогично доказывается свойство 3°.
Свойство 4° справедливо, поскольку, произведение линейных операторов заключается в их последовательном действии, и поэтому линейные операторы (АВ)С и А(ВС) совпадают и, следовательно, тождественны
Определение 1. Линейный оператор В из L(V, V) называется обратным для оператора А из L(V, V), если выполняется соотношение
АВ = ВА = I.
Обратный оператор для оператора А обычно обозначается символом А-1.
Из определения обратного оператора А следует, что для любого х Є V справедливо
соотношение А-1Ах = х.
Таким образом, если А-1Ах = 0, то х = 0, т.е. если оператор А имеет обратный, то из условия Ах = 0 следует, что х = 0.
Квадратные матрицы и n-го порядка называются подобными, если существует такая невырожденная матрица ,
Свойства подобных матриц
Свойства подобных матриц
1.Каждая квадратная матрица подобна самой себе: 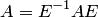 .
.
2.Если матрица 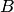 подобна матрице
подобна матрице 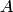 , то и
, то и 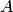 подобна
подобна 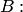
при |
. |
3. Если матрица подобна матрице , а подобна , то |
подобна |
, где . |
|
.

10.Линейные операторы в евклидовом пространстве. Сопряженные и самосопряженные операторы. Собственные векторы и собственные значения. Канонический вид матрицы.

Собственными числами матрицы 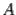 являются корни уравнения
являются корни уравнения
и только они.
Доказательство. Пусть столбец 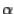 -- собственный вектор матрицы
-- собственный вектор матрицы 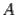 с собственным числом
с собственным числом 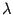 . Тогда, по определению,
. Тогда, по определению, 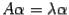 . Это равенство можно переписать в
. Это равенство можно переписать в
виде 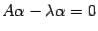 . Так как для единичной матрицы
. Так как для единичной матрицы  выполнено
выполнено 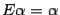 ,
,
то 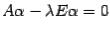 . По свойству матричного умножения
. По свойству матричного умножения 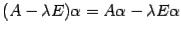 и предыдущее равенство принимает вид
и предыдущее равенство принимает вид
(19.4)
Допустим, что определитель матрицы 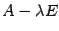 отличен от нуля,
отличен от нуля, 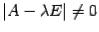 . Тогда у этой матрицы существует обратная
. Тогда у этой матрицы существует обратная 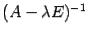 . Из равенства получим,
. Из равенства получим,
что 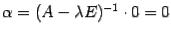 , что противоречит определению собственного вектора. Значит,
, что противоречит определению собственного вектора. Значит,
предположение, что 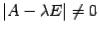 , неверно, то есть все собственные числа должны являться корнями уравнения
, неверно, то есть все собственные числа должны являться корнями уравнения  .
.
Пусть 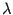 -- корень уравнения
-- корень уравнения 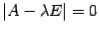 . Тогда базисный минор матрицы
. Тогда базисный минор матрицы 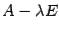 не
не
может совпадать с определителем матрицы и поэтому 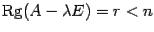 ,
,  -- порядок матрицы
-- порядок матрицы 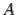 . Уравнение (19.4) является матричной записью однородной системы линейных
. Уравнение (19.4) является матричной записью однородной системы линейных
уравнений с неизвестными 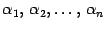 , являющимися элементами матрицы-столбца
, являющимися элементами матрицы-столбца 
. число решений в фундаментальной системе решений равно 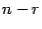 , что больше нуля. Таким образом, система (19.4) имеет хотя бы одно ненулевое решение, то есть числу
, что больше нуля. Таким образом, система (19.4) имеет хотя бы одно ненулевое решение, то есть числу 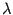 соответствует хотя бы один собственный вектор матрицы
соответствует хотя бы один собственный вектор матрицы 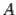 .
.
Определитель 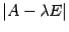 является многочленом степени
является многочленом степени 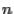 от переменного
от переменного 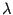 , так как при вычислении определителя никаких арифметических действий кроме сложения, вычитания и умножения выполнять не приходится.
, так как при вычислении определителя никаких арифметических действий кроме сложения, вычитания и умножения выполнять не приходится.
