I. Линейная алгебра Матрицы Прямоугольная таблица чисел

состоящая из т строк и п столбцов, называется матрицей размера n×m. Числа а₁₁, а₁₂, ..., а_mnназываются ее элементами. Таблицу, обозначающую матрицу, записывают в круглых скобках и обозначают А = (а_ij).

Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число ее строк, равное числу столбцов, - порядком квадратной матрицы.

Множество всех элементов квадратной матрицы, кото­рые лежат на отрезке, соединяющем левый верхний угол с правым нижним, называется главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним -побочной диагональю.

Квадратная матрица называется диагональной, если все ее элементы, не лежащие на главной диагонали, равны нулю. Квадратная матрица, у которой элементы, стоящие по главной диагонали равны единице, а остальные – нули, называется единичной и обозначается Е.

Две матрицы и называются равными, если число их строк и столбцов равны и если равны элементы, стоящие на соответственных местах этих мат­риц.

Матрица, все элементы которой равны нулю, назы­вается нулевой и обозначается через Н.

По определению, чтобы умножить матрицу А на число r, нужно каждый элемент матрицы А умножить на r.

Пример. Дана матрица А = , найти матрицу 3А.

Решение:

3 А = 3 =

Суммой матриц А и В называется матрица С, элементы которой равны суммам соответственных элементов матриц А и В. Складывать можно только матрицы с одинаковым числом строк и столбцов.

Пример. Даны матрицы А = иВ = . Найти матрицуС = А + В.

Решение:

С =

Свойства сложения матриц:

1. А+В=В+А

2. (А+ В) + С = А+ (В + С)

3. А + Н = А

Произведение матрицы А на матрицу В определено только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. В результате умножения получится матрица АВ, у которой столько же строк, сколько их в матрице А, и столько же столбцов, сколько их в матрице В.

Произведением двух матриц А (m×p) и В (p×n) называется матрица С (m×n), элементы которой определены по правилу

С_ij =

Замечание. Для того, чтобы перемножить две матрицы нужно элементы i-ой строки первой матрицы умножить на элементы j-ого столбца второй матрицы и сложить полученные произведения. Получим элемент новой матрицы с индексом ij.

Пример. Даны матрицы а и в. ;. Найти произведение матриц ав.

Решение:

АВ= ==

Пример . Даны матрицы А и В. А = иВ = .

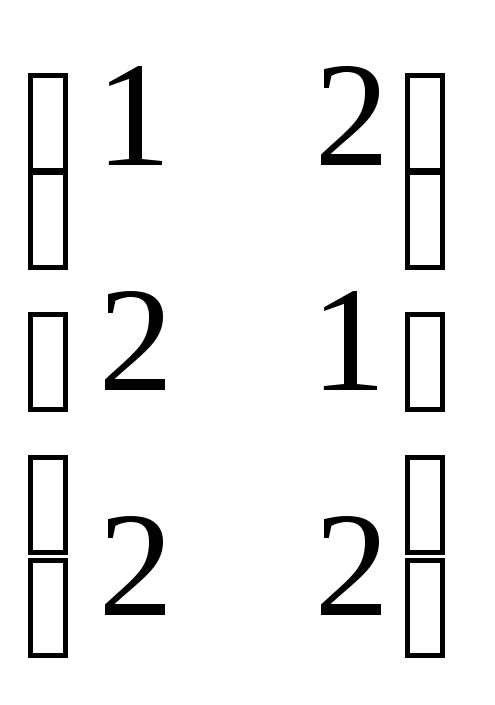Решение: А = (2X3), В = (3X2) => АВ = (2X2)

АВ= ==

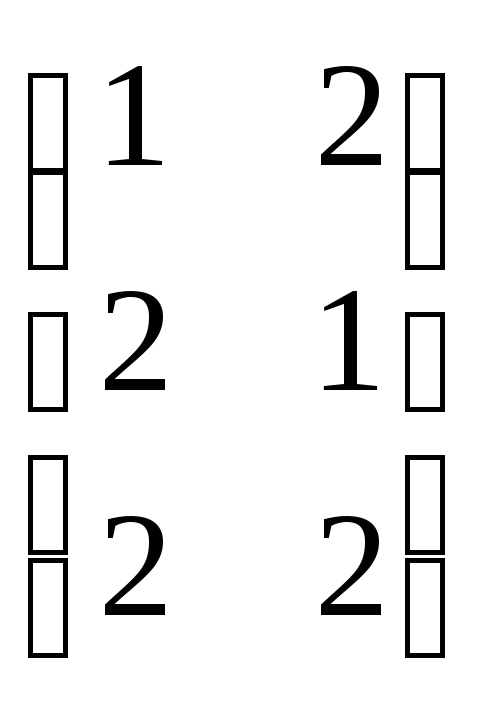Свойства умножения матриц:

1. АВВА;

2. (АВ)С=А(ВС);

3. АЕ=ЕА=А

4. (АВ)k = (AB)k= A(Bk)

5. (A+B)C = AB +BC

6. A(B+C) = AB + AC/

Транспонированной матрицей А^T называется матрица, у которой строки записаны вместо столбцов, а столбцы – вместо строк.

Пример. Пусть дана матрица А=, тогда

А^T =

Определители.

Определителем второго порядка, соответствующий матрице А =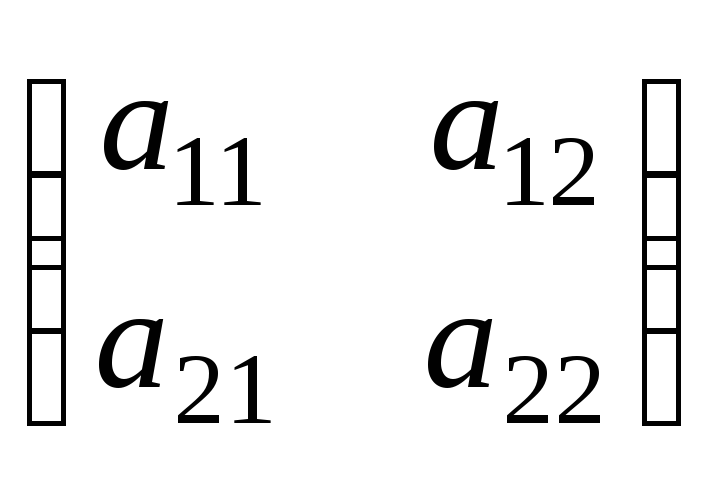, называется число=а₁₁а₂₂ - а₁₂а₂₁.

Пример. Вычислить определителем второго порядка.

= 1 · (-3) – 2 · 4 = -11.

Определителем третьего порядка, соответствующий матрице

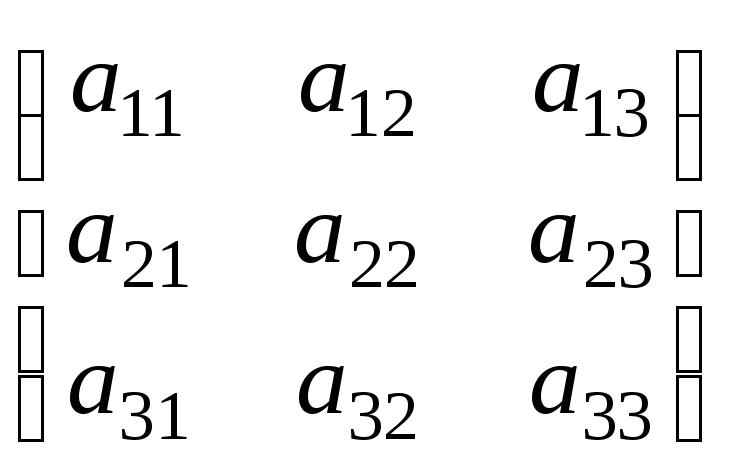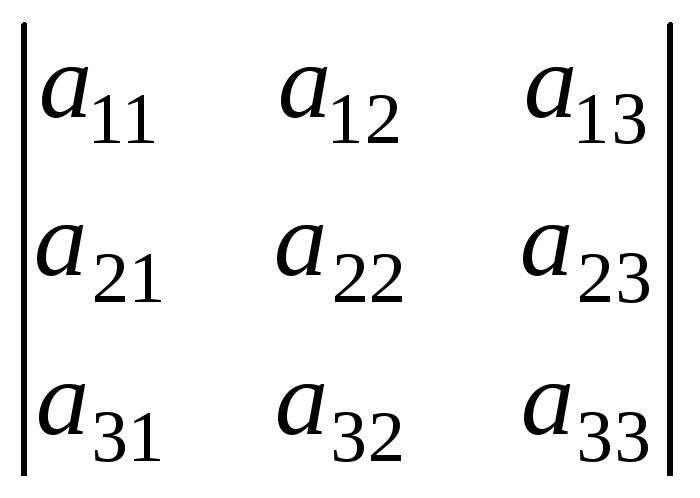А = , называется число=а₁₁а₂₂а₃₃+а₁₂а₂₃а₃₁+ а₁₃а₂₁а₃₂ - а₁₃а₂₂а₃₁ - а₁₂а₂₁а₃₃ –а₁₁ а₂₃а_32.

Чтобы запомнить какие произведения в правой части равенства следует брать со знаком «+», а какие со знаком «-», полезно правило названное правилом треугольника, изображенное на рис. 1.

« + » « - »

Рисунок 1.

Пример. Вычислить определитель

Второй способ вычисления определителей третьего порядка – это способ вычисления определителей третьего порядка, заключается в дописывании первых двух столбцов, в нахождении произведений по главной диагонали и параллелях к ней и по побочной диагонали и параллелях к ней.

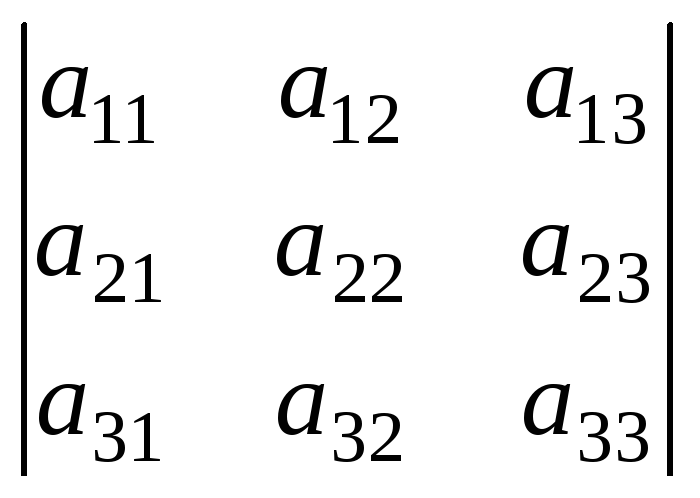
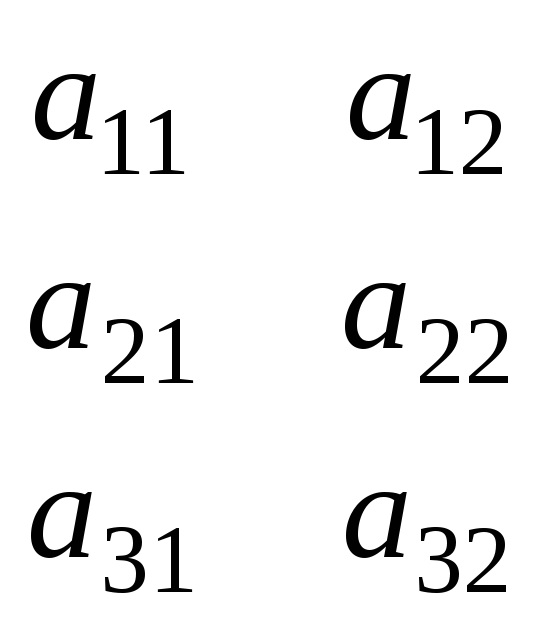= а₁₁а₂₂а₃₃+а₁₂а₂₃а₃₁+ а₁₃а₂₁а₃₂ - а₁₃а₂₂а₃₁ - а₁₂а₂₁а₃₃ –а₁₁ а₂₃а_32.

Свойства определителей:

1. Если в определителе поменять местами две строки (столбца), то его знак изменится на противоположный.

2. Если в определителе поменять местами строки и столбцы, то его знак и величина не изменится.

3. Если в определителе две строки пропорциональны (равны), то он равен нулю.

4. Если в определителе какую либо строку (столбец) умножить на некоторое число и сложить с другой строкой (столбцом), то его значение не изменится.

5. Если в определителе элементы какой либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.

6. Если определитель содержит нулевую строку или столбец, то он равен нулю.

Минором М_ij элемента определителя а_ij называется определитель, получаемый из исходного путем вычеркивания i- ой строки и j-ого столбца на которых расположен этот элемент.

Алгебраическим дополнением А_ij элемента определителя а_ij называется минор умноженный на (-1)^i+j.

Третий способ вычисления определителей – с помощью теоремы разложения.

Теорема разложения: Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.

Пример. Вычислить определитель третьего порядка, разложив определитель по элементам первой строки.

Решение:

Способ 1.

= 5· (-1)¹⁺¹· + 3 · (-1)¹⁺² · + 2·(-1)¹⁺³ · = 68.

Этот же определитель можно вычислить с помощью свойства 4), а затем применить теорему разложения. В нашем примере образуем нули в первом столбце. Для этого к элементам первой строки прибавим элементы второй строки, умноженной на 5, а к элементам третьей строки прибавим элементы второй строки, умноженной на 7. И полученную матрицу разложим по элементам первого столбца.

Решение:

Способ 2.

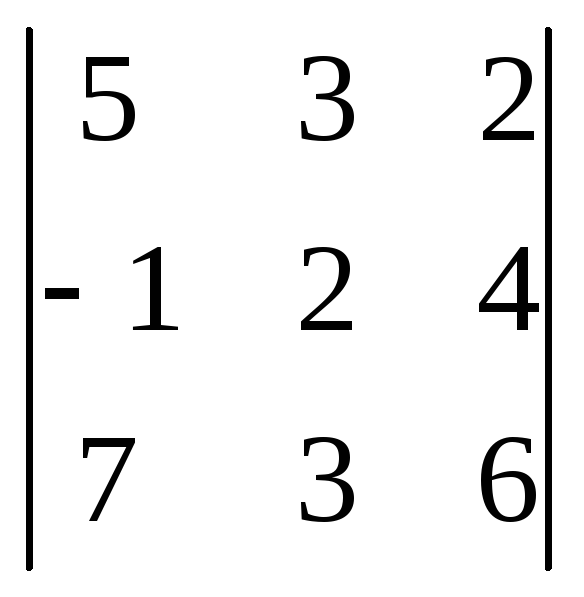= = 0- (-1)+0==13 · 34 – 17 · 22 = 68.