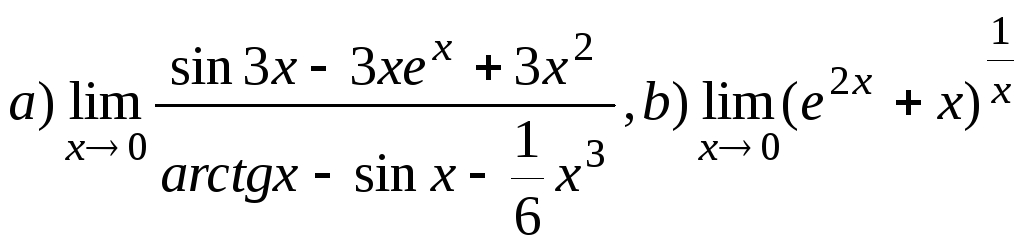- •Вопросы к зачету для заочного отделения по курсу
- •II. Векторная алгебра.
- •III. Аналитическая геометрия.
- •IV. Математический анализ
- •I. Линейная алгебра Матрицы Прямоугольная таблица чисел
- •Пример. Даны матрицы а и в. ;. Найти произведение матриц ав.
- •Определители.
- •Методы решения систем линейных уравнений.
- •Обратная матрица.
- •Решение систем уравнений матричным методом.
- •Ранг матрицы.
- •Окаймляем его слева и снизу
- •Окаймляем d3 ( это только можно сделать двумя способами)
- •Прямоугольные системы уравнений.
- •Собственные векторы и собственные значения матрицы.
- •II. Векторная алгебра.
- •Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль, равный единице. Прямоугольные координаты
- •III. Аналитическая геометрия Аналитическая геометрия на плоскости
- •Если две прямые заданы уравнениями с угловым коэффициентом
- •Если уравнения прямых заданы в общем виде
- •Приведем уравнение прямой к нормальному виду. Нормирующий множитель
- •Аналитическая геометрия в пространстве
- •Уравнение плоскости в нормальном виде
- •Уравнение плоскости в отрезках на осях
- •Угол между двумя плоскостями
- •Острый угол между прямой иплоскостью
- •Кривые второго порядка.
- •Простейшее уравнение гиперболы
- •Асимптоты гиперболы - две прямые, определяемые уравнениями
- •Простейшее уравнение параболы
- •IV. Математический анализ Функция одной переменной
- •Предел функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •Непрерывность функции
- •Дифференциальное исчисление. Производная. Техника дифференцирования. Обозначение
- •Производная сложной функции
- •Параметрически заданные функции и их дифференцирование
- •Правило Лопиталя
- •Применение дифференциального исчисления к исследованию функций
- •Признаки возрастания и убывания функций
- •Максимум и минимум функции
- •Первое достаточное условие существования экстремума функции
- •Второе достаточное условие существования экстремума
- •Асимптоты.
- •Общее исследование функции
Асимптоты.
Если расстояние d от точки кривой у = f (х), имеющей бесконечную ветвь, до некоторой определенной прямой по мере удаления точки по этой кривой в бесконечность стремится к нулю, то прямая называется асимптотой кривой.
Различают асимптоты: 1) горизонтальные, 2) вертикальные и 3) наклонные.
1.
Кривая у = f (х) имеет горизонтальную
асимптоту у =b только в том случае, когда
существует конечный предел функции f
(х) при
![]() ,
и этот предел равен b , т. е. если
,
и этот предел равен b , т. е. если
![]()
2.
Кривая у = f (х) имеет вертикальную
асимптоту х = а, если при
![]() .
Для определения вертикальных асимптот
надо отыскать те значения аргумента,
вблизи которых f (х) неограниченно
возрастает по абсолютной величине. Если
такими значениями аргумента являются
а1, а2, …, то уравнения вертикальных
асимптот будут
.
Для определения вертикальных асимптот
надо отыскать те значения аргумента,
вблизи которых f (х) неограниченно
возрастает по абсолютной величине. Если
такими значениями аргумента являются
а1, а2, …, то уравнения вертикальных
асимптот будут
х = а1, х =а2…
3. Для определения наклонной асимптоты у = kx + b кривой у = f (х) надо найти числа k и b из формул
![]()
![]()
(следует
отдельно рассматривать случаи
![]() ).
Наклонные асимптоты у кривой у = f (х)
существуют в том и только в том случае,
когда эти пределы имеют конечное
значение. При определении этих пределов
удобно пользоваться правилом Лопиталя.
).
Наклонные асимптоты у кривой у = f (х)
существуют в том и только в том случае,
когда эти пределы имеют конечное
значение. При определении этих пределов
удобно пользоваться правилом Лопиталя.
Пример.
Найти асимптоты кривой
![]()
Решение. Горизонтальных асимптот нет. Вертикальную асимптоту находим из условия
2х
+ 3 = 0 => х = - 3/2, при этом у
![]() ,
когда
,
когда![]() ,
у
,
у![]() ,
когда
,
когда![]() .
Определим наклонные асимптоты , уравнение
которых имеет вид: у = kx + b
.
Определим наклонные асимптоты , уравнение
которых имеет вид: у = kx + b
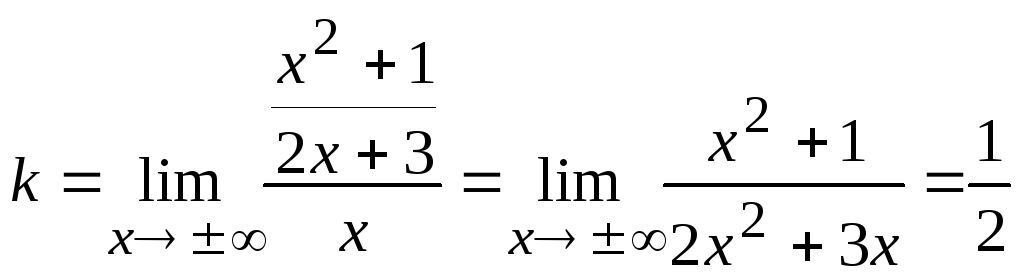
![]()
Так
как k и b имеют конечные значения и равны
между собой при х![]() и при х
и при х![]() ,
то имеется единственная наклонная
асимптота, уравнение которой
,
то имеется единственная наклонная
асимптота, уравнение которой
![]()
Общее исследование функции
Под полным исследованием функции обычно понимается решение таких вопросов:
Определение области существования функции.
Выявление вопроса о четности и нечетности функции.
Определение точек разрыва функции.
Определение асимптот графика функции.
Определение интервалов возрастания и убывания функции.
Определение экстремума функции.
Определение интервалов выпуклости и вогнутости графика функции.
Определение точек перегиба.
Нахождение пересечения с осями координат.
Построение графика функции.
Пример.
Исследуем функцию
![]()
D
(y) = (![]() ).
Функция непрерывна на всей области
определения. Точек разрыва нет.
).
Функция непрерывна на всей области
определения. Точек разрыва нет.
Функция не является ни четной, ни нечетной, ни периодической.
Точек разрыва нет.
Вертикальных
асимптот нет;![]() ,
наклонных асимптот нет.
,
наклонных асимптот нет.
5,
6.
![]() .
Критические точки х = -2, х = 0.
.
Критические точки х = -2, х = 0.
|
х |
( |
-2 |
(-2, 0) |
0 |
( |
|
Знак
|
+ |
|
- |
|
+ |
|
Поведение функции |
Возрастает |
max
3 |
Убывает |
min 0 |
Возрастает |
7,
8.
![]() ,
,![]() при
х = 1,
при
х = 1,![]() не существует при х = 0.
не существует при х = 0.
|
х |
( |
0 |
( 0, 1) |
0 |
( |
|
Знак
|
- |
|
- |
|
+ |
|
Поведение функции |
Выпукла верх |
Не является точкой перегиба |
Выпукла верх |
Точка перегиба у = 6 |
Выпукла вниз |
9.
![]() х
=0 и х = -5.
х
=0 и х = -5.
10.

Задание 1
Вычислить определитель матрицы А второго порядка
Вычислить определитель матрицы В третьего порядка
Вычислить определитель матрицы В, разложив его по какой-либо строке и какому либо столбцу
Вычислить определитель матрицы В, пользуясь свойствами определителей. Свести вычисление определителя третьего порядка к вычислению одного определителя второго порядка
|
Вариант 1 |
|
|
|
|
|
|
|
|
|
| ||||||||
|
A = |
( |
-3 |
-6 |
) |
|
B = |
( |
3 |
-1 |
4 |
) | |||||||
|
3 |
2 |
|
0 |
2 |
-5 | |||||||||||||
|
|
|
|
|
|
|
1 |
-2 |
-4 | ||||||||||
|
Вариант 2 |
|
|
|
|
|
|
|
|
|
| ||||||||
|
A = |
( |
8 |
7 |
) |
|
B = |
( |
-1 |
-4 |
-4 |
) | |||||||
|
-9 |
-3 |
|
-4 |
-1 |
0 | |||||||||||||
|
|
|
|
|
|
|
-1 |
3 |
-2 | ||||||||||
|
Вариант 3 |
|
|
|
|
|
|
|
|
|
| ||||||||
|
A = |
( |
-1 |
0 |
) |
|
B = |
( |
-5 |
2 |
-3 |
) | |||||||
|
-1 |
-8 |
|
1 |
-4 |
-4 | |||||||||||||
|
|
|
|
|
|
|
-3 |
-1 |
0 | ||||||||||
|
Вариант 4 |
|
|
|
|
|
|
|
|
|
| ||||||||
|
A = |
( |
-10 |
-7 |
) |
|
B = |
( |
0 |
-1 |
-2 |
) | |||||||
|
7 |
7 |
|
-3 |
2 |
1 | |||||||||||||
|
|
|
|
|
|
|
-5 |
-5 |
2 | ||||||||||
|
Вариант 5 |
|
|
|
|
|
|
|
|
|
| ||||||||
|
A = |
( |
1 |
6 |
) |
|
B = |
( |
-4 |
-4 |
-1 |
) | |||||||
|
-5 |
2 |
|
2 |
-1 |
-3 | |||||||||||||
|
|
|
|
|
|
|
2 |
0 |
-5 | ||||||||||
|
Вариант 6 |
|
|
|
|
|
|
|
|
|
| ||||||||
|
A = |
( |
-8 |
-1 |
) |
|
B = |
( |
1 |
2 |
0 |
) | |||||||
|
3 |
-3 |
|
-2 |
-4 |
2 | |||||||||||||
|
|
|
|
|
|
|
0 |
-4 |
-3 | ||||||||||
|
Вариант 7 |
|
|
|
|
|
|
|
|
|
| ||||||||
|
A = |
( |
3 |
-8 |
) |
|
B = |
( |
-3 |
-1 |
1 |
) | |||||||
|
-9 |
-8 |
|
3 |
2 |
-2 | |||||||||||||
|
|
|
|
|
|
|
-2 |
1 |
-1 | ||||||||||
|
Вариант 8 |
|
|
|
|
|
|
|
|
|
| |
|
A = |
( |
-6 |
5 |
) |
|
B = |
( |
2 |
-4 |
2 |
) |
|
-1 |
7 |
|
-1 |
-1 |
3 | ||||||
|
|
|
|
|
|
|
-4 |
-3 |
1 | |||
|
Вариант 9 |
|
|
|
|
|
|
|
|
|
| |
|
A = |
( |
5 |
-2 |
) |
|
B = |
( |
-2 |
2 |
3 |
) |
|
7 |
2 |
|
-5 |
-4 |
-1 | ||||||
|
|
|
|
|
|
|
3 |
2 |
3 | |||
|
Вариант 10 |
|
|
|
|
|
|
|
|
|
| |
|
A = |
( |
-4 |
-9 |
) |
|
B = |
( |
3 |
-1 |
-5 |
) |
|
-5 |
-3 |
|
0 |
2 |
-5 | ||||||
|
|
|
|
|
|
|
1 |
-2 |
-4 | |||
Задание 2
1. Решить методом Крамера систему уравнений Ах = а
Решить методом Крамера систему уравнений Вx = b
Решить методом Гаусса систему уравнений Вx = b
|
Вариант |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
1 |
-3 |
2 |
) |
b= |
( |
13 |
) |
|
A = |
( |
1 |
3 |
) |
a= |
( |
-5 |
) |
4 |
0 |
-1 |
-8 | ||||||
|
2 |
-1 |
11 |
3 |
-2 |
-1 |
-3 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
-4 |
1 |
-3 |
) |
b= |
( |
24 |
) |
|
A = |
( |
3 |
1 |
) |
a= |
( |
5 |
) |
-1 |
-5 |
3 |
21 | ||||||
|
-4 |
-2 |
-6 |
-2 |
2 |
3 |
-9 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
0 |
-4 |
1 |
) |
b= |
( |
-5 |
) |
|
A = |
( |
-4 |
-1 |
) |
a= |
( |
-1 |
) |
3 |
-1 |
-2 |
1 | ||||||
|
-1 |
-3 |
-3 |
2 |
-3 |
-2 |
-1 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
-5 |
0 |
-4 |
) |
b= |
( |
16 |
) |
|
A = |
( |
-2 |
-3 |
) |
a= |
( |
-5 |
) |
-2 |
3 |
2 |
4 | ||||||
|
2 |
-4 |
-16 |
-3 |
1 |
2 |
12 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
-1 |
-5 |
0 |
) |
b= |
( |
24 |
) |
|
A = |
( |
0 |
-5 |
) |
a= |
( |
20 |
) |
2 |
-2 |
-3 |
3 | ||||||
|
-4 |
-5 |
36 |
1 |
-4 |
-3 |
12 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
3 |
-1 |
-5 |
) |
b= |
( |
10 |
) |
|
A = |
( |
2 |
2 |
) |
a= |
( |
2 |
) |
-3 |
2 |
1 |
7 | ||||||
|
-1 |
3 |
-9 |
-4 |
0 |
1 |
8 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
-2 |
3 |
-1 |
) |
b= |
( |
-8 |
) |
|
A = |
( |
-5 |
0 |
) |
a= |
( |
-5 |
) |
1 |
-3 |
-4 |
16 | ||||||
|
2 |
2 |
2 |
0 |
-5 |
-4 |
18 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
2 |
-2 |
3 |
) |
b= |
( |
6 |
) |
|
A = |
( |
-3 |
-2 |
) |
a= |
( |
-1 |
) |
-4 |
1 |
0 |
3 | ||||||
|
-4 |
1 |
6 |
-5 |
-1 |
0 |
15 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
-3 |
2 |
-2 |
) |
b= |
( |
-11 |
) |
|
A = |
( |
-1 |
-4 |
) |
a= |
( |
23 |
) |
0 |
-4 |
-5 |
-14 | ||||||
|
-1 |
0 |
3 |
-1 |
3 |
-5 |
-10 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
1 |
-3 |
2 |
) |
b= |
( |
-5 |
) |
|
A = |
( |
1 |
3 |
) |
a= |
( |
-14 |
) |
-5 |
0 |
-1 |
10 | ||||||
|
2 |
-1 |
-7 |
3 |
-2 |
-1 |
6 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 3.
Решить матричным методом систему уравнений Ах = а
Решить матричным методом систему уравнений Вx = b
|
Вариант |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
3 |
-3 |
1 |
) |
b= |
( |
7 |
) |
|
A = |
( |
2 |
-1 |
) |
a= |
( |
11 |
) |
|
2 |
1 |
-2 |
-12 | ||||||
|
4 |
-3 |
25 |
|
1 |
-2 |
1 |
7 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
0 |
3 |
-1 |
) |
b= |
( |
1 |
) |
|
A = |
( |
-5 |
-3 |
) |
a= |
( |
6 |
) |
|
-2 |
0 |
-4 |
0 | ||||||
|
-2 |
-5 |
10 |
|
3 |
1 |
-1 |
-13 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
-3 |
0 |
-3 |
) |
b= |
( |
-6 |
) |
|
A = |
( |
-3 |
-5 |
) |
a= |
( |
17 |
) |
|
3 |
-1 |
3 |
11 | ||||||
|
1 |
2 |
-6 |
|
-4 |
-5 |
-3 |
17 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
3 |
-3 |
-5 |
) |
b= |
( |
13 |
) |
|
A = |
( |
-1 |
2 |
) |
a= |
( |
-1 |
) |
|
-1 |
-2 |
1 |
3 | ||||||
|
-5 |
0 |
-5 |
|
-2 |
-2 |
-5 |
16 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
0 |
3 |
2 |
) |
b= |
( |
-5 |
) |
|
A = |
( |
1 |
0 |
) |
a= |
( |
-3 |
) |
|
-5 |
-3 |
-1 |
21 | ||||||
|
-2 |
-2 |
4 |
|
0 |
1 |
2 |
-7 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
-3 |
0 |
0 |
) |
b= |
( |
-6 |
) |
|
A = |
( |
3 |
-2 |
) |
a= |
( |
2 |
) |
|
0 |
-4 |
-3 |
11 | ||||||
|
1 |
-4 |
-6 |
|
2 |
-5 |
0 |
29 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
3 |
-3 |
-2 |
) |
b= |
( |
1 |
) |
|
A = |
( |
-4 |
-4 |
) |
a= |
( |
-4 |
) |
|
-4 |
-5 |
-5 |
9 | ||||||
|
-5 |
3 |
19 |
|
-5 |
-2 |
-2 |
7 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
0 |
3 |
-4 |
) |
b= |
( |
7 |
) |
|
A = |
( |
-2 |
3 |
) |
a= |
( |
-21 |
) |
|
1 |
3 |
2 |
-3 | ||||||
|
-2 |
1 |
-11 |
|
-3 |
1 |
-4 |
17 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
-3 |
0 |
3 |
) |
b= |
( |
-15 |
) |
|
A = |
( |
0 |
1 |
) |
a= |
( |
-4 |
) |
|
-3 |
2 |
0 |
-16 | ||||||
|
1 |
-1 |
3 |
|
-1 |
-5 |
3 |
14 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B = |
( |
3 |
-3 |
1 |
) |
b= |
( |
-2 |
) |
|
A = |
( |
2 |
-1 |
) |
a= |
( |
-7 |
) |
|
2 |
1 |
-2 |
6 | ||||||
|
-5 |
-3 |
34 |
|
1 |
-2 |
1 |
-2 |
Задание 4.
Вычислить ранг матрицы.
1. ,
2.
,
2. ;
;
3.
 4.
4.
5. 6.
6.
7. 8
8
9.
 10.
10.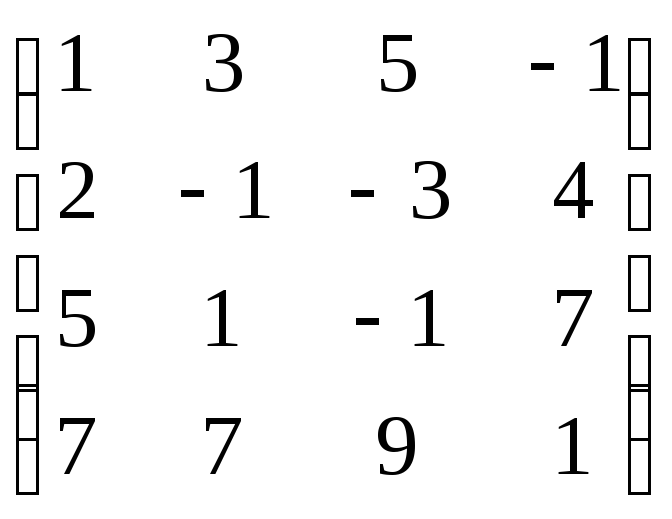
Задание 5
Даны две вершины треугольника Δ АВС: А (х1,у1), В (х2,у2) и точка D (x3,y3)пересечения высот:
а) составить уравнение высот, медиан, биссектрис треугольника Δ АВС.
б) найти уравнения прямых, проходящих через вершины треугольника и параллельных сторонам.
в) определить длины высот треугольника и расстояние от точки М (х4, у4) до сторон треугольника.
|
n |
x1 |
y1 |
x2 |
y2 |
x3 |
y3 |
x4 |
y4 |
|
|
2 |
5 |
0 |
7 |
2 |
2 |
7 |
1 |
|
|
4 |
10 |
4 |
2 |
8 |
4 |
9 |
6 |
|
|
4 |
6 |
5 |
6 |
9 |
4 |
2 |
10 |
|
|
7 |
4 |
5 |
10 |
4 |
4 |
7 |
8 |
|
|
6 |
-2 |
8 |
2 |
6 |
8 |
10 |
3 |
|
|
1 |
8 |
2 |
4 |
9 |
5 |
5 |
9 |
|
|
6 |
6 |
5 |
4 |
9 |
5 |
4 |
9 |
|
|
7 |
2 |
7 |
5 |
3 |
1 |
2 |
3 |
|
|
8 |
6 |
4 |
10 |
5 |
5 |
5 |
6 |
|
|
7 |
3 |
6 |
-3 |
5 |
8 |
4 |
1 |
Задание 6.
Даны координаты вершин пирамиды АВСD: А (х1,у1,z1), В (х2,у2,z3) ,C (x2,y2,z2) ,D (х4, у4,z3)
Найти:
1) длину ребра АВ;.
2) угол между ребрами АВ и АD;
3) угол меду ребром AD и гранью ABC;
4) площадь грани ABC;
5) объем пирамиды;
6) уравнение прямой AB;
7) уравнение плоскости ABC;
8) уравнение высоты, опущенной из вершиныD на грань ABC.
-
n
x1
y1
z1
x2
y2
z2
x3
y3
z3
x4
y4
z4
1
1
1
7
5
6
0
-5
4
1
2
3
4
2
2
3
0
1
-1
4
2
5
7
8
3
-5
2
4
5
1
-3
0
4
4
5
6
-2
3
5
1
-3
4
7
8
-1
5
7
8
2
4
-6
1
3
5
0
2
0
0
12
-6
4
3
-1
5
0
4
2
1
2
0
1
6
3
4
-3
-5
5
0
2
1
-4
8
16
7
-2
1
7
3
-3
18
5
4
-1
18
0
25
1
0
5
3
2
7
5
0
9
1
2
-12
2
1
0
4
3
-3
-6
5
17
30
2
1
Задание 7.
Составить уравнение линии, для каждой точки которой отношений расстояние до точки А (3,0) и до прямой х = 12 равно ε = 0,5 полученное уравнение привести к простейшему виду и построить прямую.
Составить уравнение линии, для каждой точки которой отношений расстояние до точки А (-3,4) равно расстоянию до прямой у = 2. Полученное уравнение привести к простейшему виду и построить прямую.
Показать, что
 есть
уравнение окружности. Найти ее центр
и радиус.
есть
уравнение окружности. Найти ее центр
и радиус.Написать уравнение окружности, проходящей через точки: (0,1), (2,0), (3,1).
Гипербола проходит через точки (3,
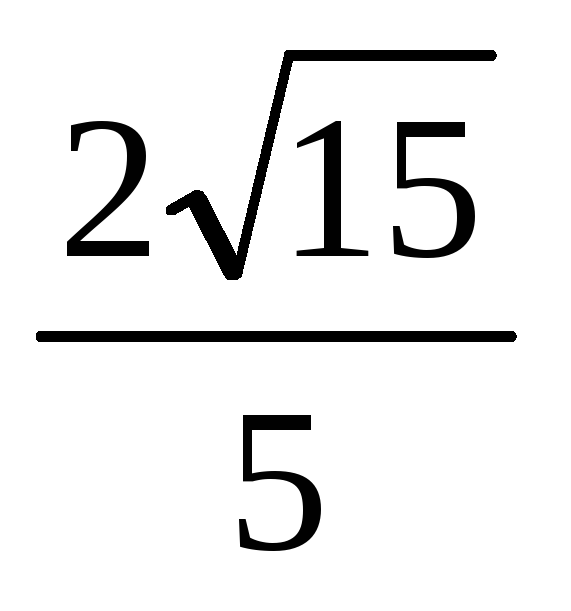 )
и (
)
и (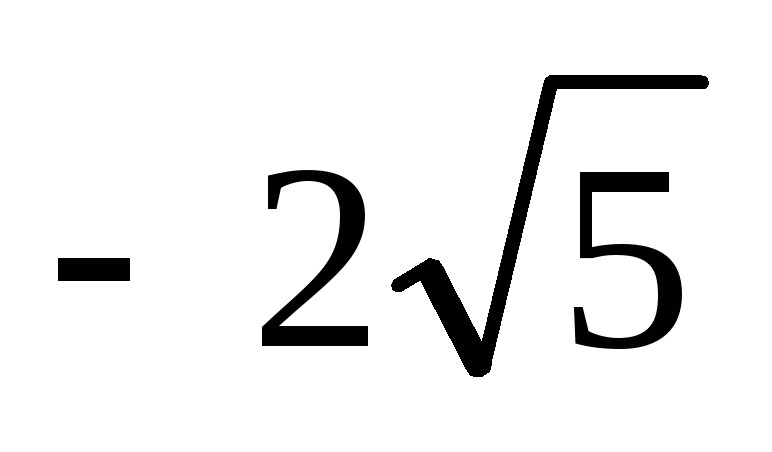 ,3).
Найти уравнение гиперболы.
,3).
Найти уравнение гиперболы.Найти уравнение асимптот гиперболы
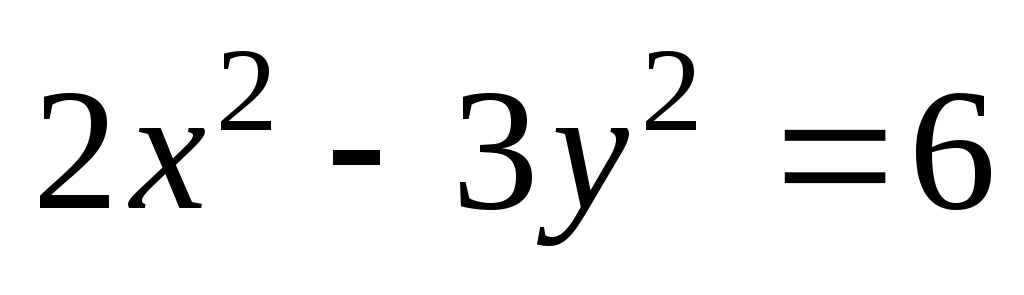 .
.Найти острый угол между асимптотами гиперболы, если ее эксцентриситет равен 2.
Дана равнофокусная гипербола
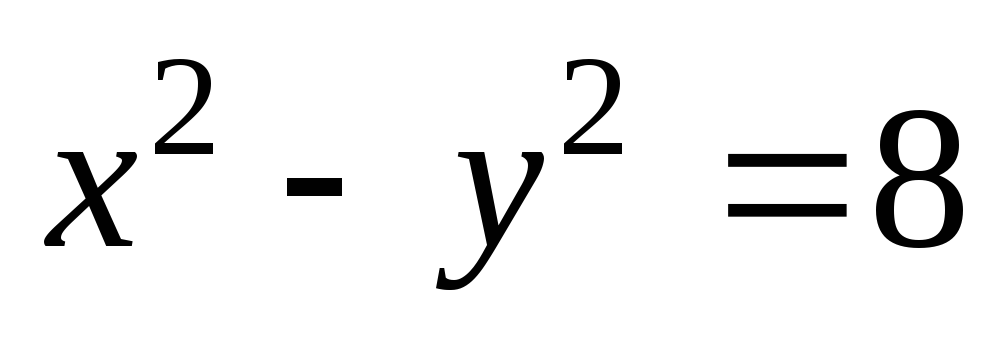 .
Найти уравнение эллипса, фокусы которого
находится в фокусах гиперболы, если
известно, что эллипс проходит через
точкуА
(4,6).
.
Найти уравнение эллипса, фокусы которого
находится в фокусах гиперболы, если
известно, что эллипс проходит через
точкуА
(4,6).Составить уравнение параболы, зная, что вершина ее находится в начале координат и расстояние от фокуса до вершины равно 4 единицам длины, а осью симметрии служит ось Ох.
Парабола симметрична относительно оси Ох , проходит через точку А (4,-1), а вершина ее лежит в начале координат. составить ее уравнение.
Задание 8. Найти область определения функции
1.
![]()
2.
![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.![]()
10.![]()
Задание 9.Построить график функции
1.![]()
2.![]()
3.![]()
4
![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.![]()
10.
![]()
Задание 10 .Найти пределы функции
1.а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
2.а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
3.а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
4.
а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
5.а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
6.а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
7.
а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
8.а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
9.а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
10.а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]()
Задание 11. Найти производную
1.![]() ,
б)
,
б)![]() ,
,
в)
![]() ,
г)
,
г)![]() ,
д)
,
д)![]() ,
е)
,
е)![]()
2.
а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]() ,е)
,е)![]()
3.
а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
г)
,
г)![]() ,
д)
,
д)![]() ,
e)
,
e)![]()
4.
а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]() ,
e)
,
e)![]()
5.
а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
г)
,
г)![]() ,
д)
,
д)![]() ,
,
е)
![]()
6.
а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
г)
,
г)![]() ,
д)
,
д)![]() ,
,
е)
![]()
7.
а)
![]() ,
б)
,
б)![]() ,
,
в)
![]() ,
г)
,
г)![]() ,
д)
,
д)![]() ,
,
е)
![]()
8.
а)
![]() ,
б)
,
б)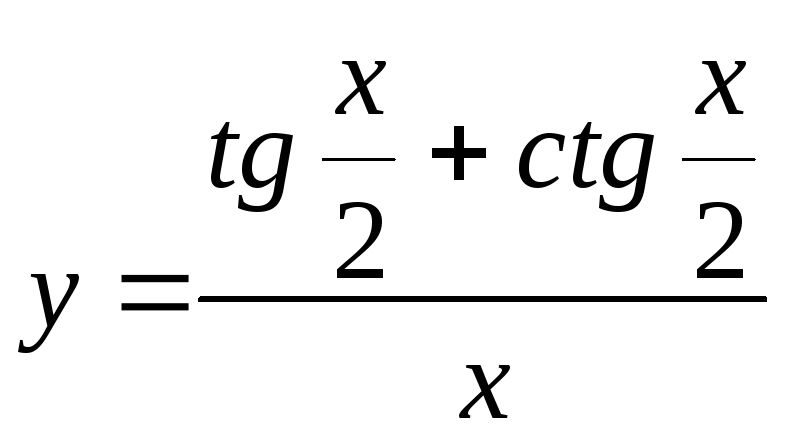 ,
в)
,
в)![]() ,
г)
,
г)![]() ,
д)
,
д)![]() ,
,
е)
![]()
9.
а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]() ,
е)
,
е)![]()
10.
а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)
![]() ,
д)
,
д)![]() ,
е)
,
е)![]()
Задание 12. Показать, что функция удовлетворяет равенству
Задание 13. Найти вторую производную функции, заданной параметрически.
1 .
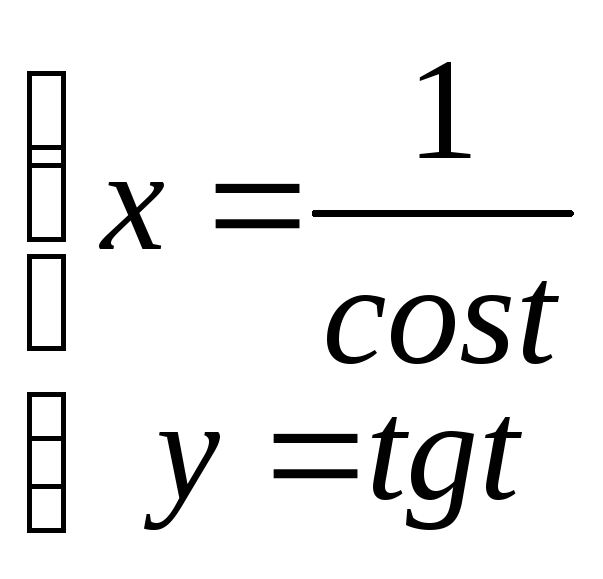 6.
6.![]()
2.
![]() 7
7![]()
3.
![]() 8
8![]()
4.
![]() 9.
9.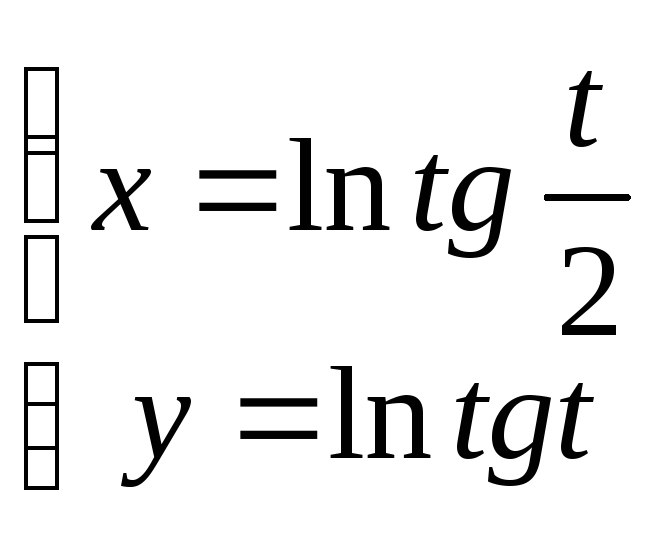
5.
![]() 10.
10.![]()
Задание 14. Найти пределы, пользуясь правилом Лопиталя
Задание 15. Найти экстремумы заданных функций.
1.![]() 6.
6.![]()
2.![]() 7.
7.![]()
3.![]() 8.
8.![]()
4.![]() 9.
9.![]()
5.![]() 10.
10.![]()
Задание 16. Найти наибольшее и наименьшее значение на указанных отрезках и на указанных интервалах.

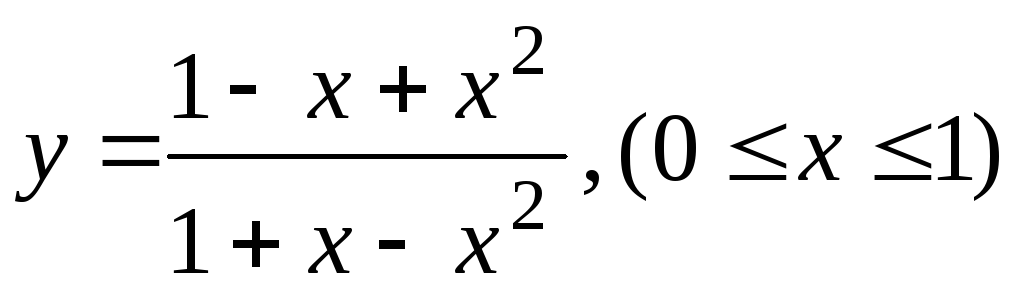
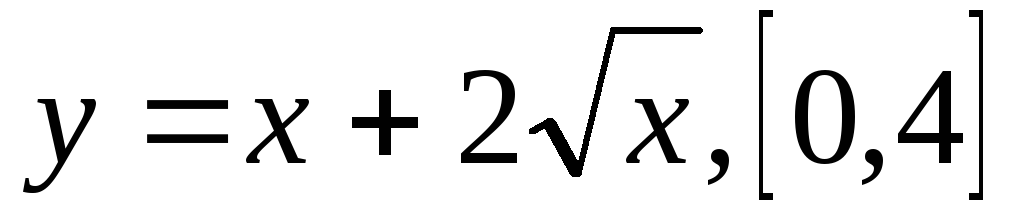
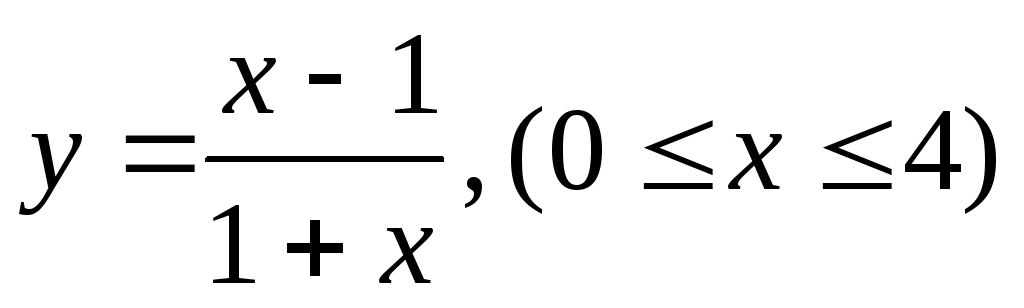
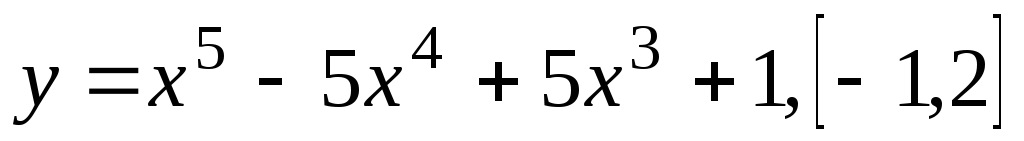
.
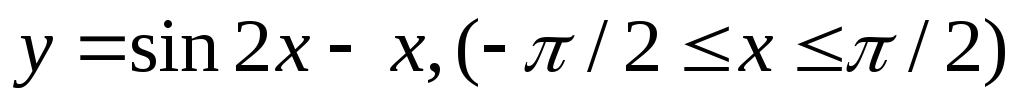
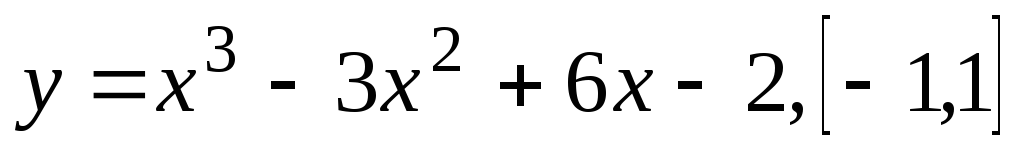
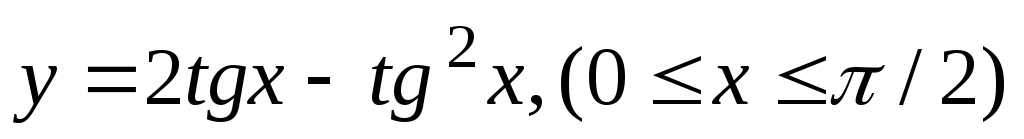

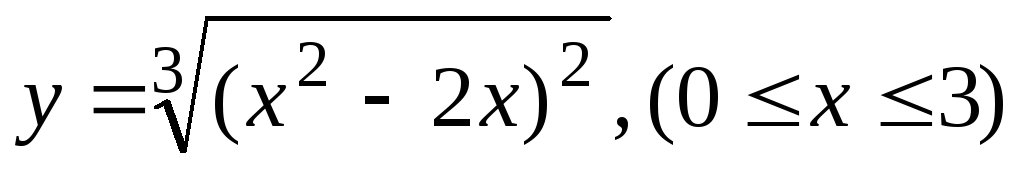
Задание 17. Провести полное исследование данных функций и начертить их графики.
1.![]() 6.
6.![]()
2.![]() 7.
7.![]()
3.![]() 8.
8.![]()
4.![]() 9.
9.![]()
5.![]() 10.
10.![]()
Литература:
Баврин И.И. Курс высшей математики.-М.:Просвящение,1992.-400 с.
Бронштейн И.Н., Семендяев К.А. Справочник по математике. М, 1967г,608 с
Общий курс высшей математики для экономистов, под ред В .И .Ермакова-М. «Инфра-М».1999 г.-655 с.
Теуш В.Л. Курс высшей математики. - М.: Советская наука, 1958г, 270 с.
Шипачев В.С. Высшая математика: Учебное пособие М. Высшая школа,1990.-479с.
Высшая математика для экономистов: Учебник для вузов/Н.Ш.Кремер, Б.А.Путко и др.; М: ЮНИТИ, 2002. – 461 с.
Валєєв К.Г, Джалладова І.А Вища математика: Навч. Посібник: