
Вказівки до лаб_2010
.pdf
Рис. 61. Побудова кореляційної матриці.
Рис. 62. Коваріаційна і кореляційна матриці.
Звідси видно, що вибіркові коваріаційна та кореляційна матриці
æ |
6,13 |
0,80 |
4,87 |
ö |
æ |
1 |
0,25 |
0,92 |
ö |
||||
|
|
ç |
0,80 |
1,60 |
0,73 |
÷ |
|
|
ç |
0,25 |
1 |
0,27 |
÷ |
|
|
|
|||||||||||
S = ç |
÷ |
та R = ç |
÷ |
||||||||||
ç |
4,87 |
0,73 |
4,60 |
÷ |
ç |
0,92 |
0,27 |
1 |
÷ |
||||
è |
ø |
è |
ø |
||||||||||
симетричні. Бачимо, що вибіркова дисперсія змінної Y D(Y ) = 6,13, а вибіркові дисперсії змінних X1 та X2 — менші і становлять, відповідно, 1,60 та 4,60.
Діагональні елементи вибіркової кореляційної матриці R дорівнюють 1. У вибірковій кореляційній матриці найбільша лінійна кореляція простежується між змінними Y та X2 . Кореляція між незалежними змінними X1 та X2 не-
значна (0,27).
81

Крок 3. Для знаходження вибіркового рівняння множинної лінійної ре-
гресії yˆ = β0 + β1x1 + β2 x2 та його аналізу скористатися процедурою Regression
надбудови Data Analysis. Основними елементами діалогового вікна Regression
(рис. 62) є:
Рис. 63. Побудова множинного лінійного рівняння регресії.
∙ Іnput Y Range — діапазон значень змінної Y ;
∙ Іnput X Range — діапазон значень змінних X1 та X2 водночас;
∙ Labels — відмітити цю опцію лише в тому випадку, коли значення змінних Y , X1 , X2 в полях Іnput Y Range та Іnput X Range вводяться разом із заго-
ловками (Y , X1 , X2 );
∙Constant is Zero — відмітити цю опцію лише в тому випадку, коли припус-
кається, що вільний член рівняння регресії β0 = 0 ;
∙Confidence Level — цю опцію виставити тільки в тому випадку, коли потрібно знайти не тільки 95 %-ні довірчі інтервали для коефіцієнтів регресії, а й
90 %-ні, 98 %-ні, 99 %-ні тощо;
∙Output Range — адреса результуючої клітинки.
82

Зауважимо, що для глибшого аналізу регресійної моделі можна розглядати в діалоговому вікні Regression елементи Residuals (для аналізу залишків) та Normal Probability (для порівняння з нормальним розподілом).
Крок 4. Натиснути ОК та проаналізувати отримані результати (рис. 64).
Рис. 64. Моделювання множинної лінійної регресії.
Отже, вибіркове рівняння множинної лінійної регресії має вигляд yˆ = 9,15 + 0,02x1 +1,06x2 . Для цього рівняння модуль множинного коефіцієнта кореляції дорівнює 0,92, що свідчить про значний сумісний вплив факторів X1 ,
X2 на Y . Коефіцієнт детермінації R2 = 0,84. Вправлений коефіцієнт де-
термінації R%2 = 0,79 , а це означає, що 79 % варіації результативної змінної Y
пояснюється варіацією факторних змінних X1 , X2 ; решта 21 % цієї варіації припадає на вплив випадкових, не врахованих у регресійній моделі факторів. Стандартна похибка регресії σε = 1,18. p -значення для F -статистики Фішера дорівнює 0,0016, що менше за заданий рівень значущості 0,05, а це означає, що коефіцієнт детермінації значущий на рівні 0,05. p -значення для коефіцієнтів β1
(при змінній X1 ) та β2 (при змінній X2 ) дорівнюють, відповідно, 0,9563 та
83
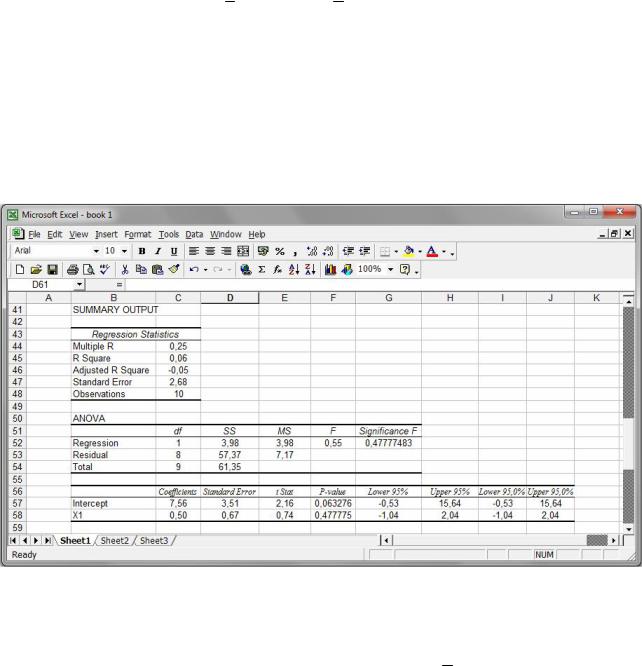
0,0006, а це означає, що коефіцієнт β1 незначущий на рівні 0,05, а β2 — значу-
щий. Незначущість коефіцієнта β1 дозволяє зробити висновки про неадекват-
ність побудованого рівняння регресії. А це, в свою чергу, означає, що коефіцієнти рівняння регресії β1 = 0,02 та β2 =1,06 не мають жодного еко-
номічного змісту. Відповідно, прогнозування середнього значення залежної змінної Y на основі побудованого рівняння регресії є неможливим.
Крок 5. Виключимо з розгляду змінну X2 та побудуємо вибіркове рівнян-
ня парної лінійної регресії, яке характеризує залежність середнього значення змінної Y від значень фактора X1 (рис. 65).
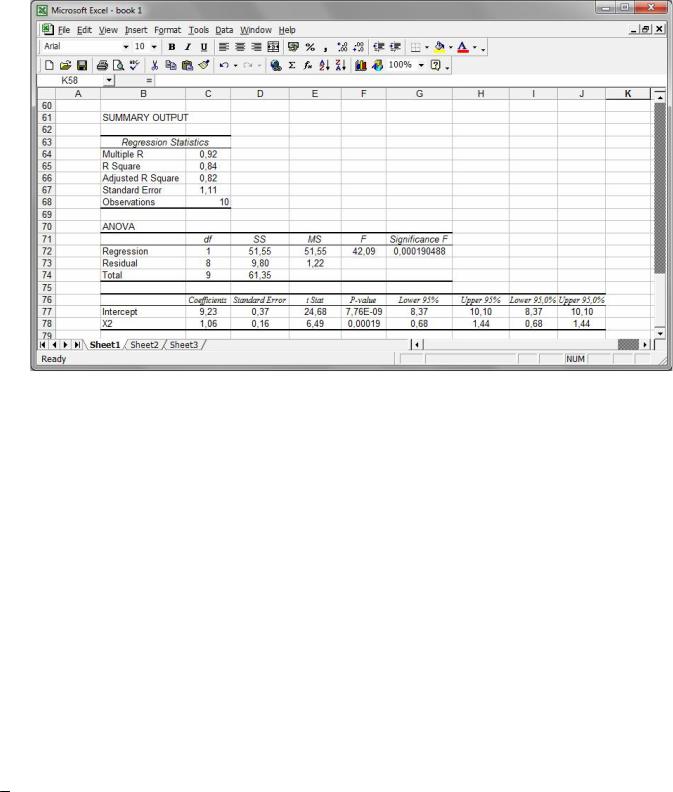
Рис. 65. Виключення з розгляду змінної X2 .
Отримаємо рівняння регресії yˆ = 7,56 + 0,50x1. Проте це рівняння внаслідок великих (більших за α = 0,05 ) p -значень для коефіцієнта β1 та коефіцієнта де-
термінації R2 ( p = 0,4778 ) виявляється неадекватним до результатів спостере-
жень.
84
Крок 6. Виключимо з розгляду змінну X1 та побудуємо вибіркове рівнян-
ня парної лінійної регресії, яке характеризує залежність середнього значення змінної Y від значень фактора X2 (рис. 66).
Рис. 66. Виключення з розгляду змінної X1 .
Отримаємо рівняння регресії yˆ = 9,23 +1,06x2 . Для |
цього рівняння p - |
||
|
|
та коефіцієнта детермінації R2 |
( p = 0,00019 ) є до- |
значення для коефіцієнта β |
|||
1 |
|
||
статньо малими (меншими за заданий рівень значущості α = 0,05 ), тому знай-
дене рівняння yˆ = 9,23 +1,06x2 є адекватним.
Із рис. 66 видно, що модуль коефіцієнта кореляції дорівнює 0,92, що свід-
чить про значний вплив фактора X2 на Y . Коефіцієнт детермінації R2 = 0,84,
виправлений коефіцієнт детермінації R%2 = 0,82, а це означає, що 82 % варіації
результативної змінної Y пояснюється варіацією факторної змінної X2 ; решта
18 % цієї варіації припадає на вплив випадкових, не врахованих у регресійній моделі факторів. Стандартна похибка регресії σε = 1,11. Коефіцієнт регресії
β1 =1,06 вказує на те, що згідно зі знайденою регресійною моделлю при збіль-
шенні фактора X2 на 1 одиницю значення фактора Y збільшується в середньо-
85
му на 1,06 одиниць. 95 %-ні довірчі інтервали для коефіцієнтів β0 та β1 теоре-
тичного рівняння регресії мають вигляд
8,37 < β0 < 10,10; 0,68 < β1 < 1,44 .
Про значущість коефіцієнтів β0 , β1 свідчить також те, що зазначені довірчі ін-
тервали для них не „накривають” число |
0. |
|
|
||
Висновок. Із розглянутих нами множинної лінійної регресійної моделі |
|||||
yˆ = 9,15 + 0,02x1 +1,06x2 |
і |
парних |
лінійних |
регресійних |
моделей |
yˆ = 7,56 + 0,50x1 та yˆ = 9,23 |
+1,06x2 адекватною виявилась лише остання. Це |
||||
означає, що: |
|
|
|
|
|
∙змінна X2 чинить кореляційний вплив на змінну Y ;
∙змінна X1 не чинить кореляційного впливу на залежну змінну Y ;
∙змінні X1 та X2 не справляють сукупного кореляційного впливу на змін-
ну Y .
Лабораторна робота № 9
Множинна нелінійна регресія
Основні поняття
Досліджуючи моделі простої і множинної регресії, ми припускали, що зв’язок між результативною ознакою та кожним із факторів є лінійним. Однією із найпоширеніших нелінійних залежностей між ознаками D, P, M є степенева модель
D = αPβ1 M β2 .
Прологарифмувавши
ln D = lnα + β1 ln P + β2 ln M
і провівши заміну змінних Y = ln D, b0 = lnα , X1 = ln P, X2 = ln M , отримаємо рівняння множинної лінійної регресії:
Y = β0 + β1X1 + β2 X2 .
86
Від останнього рівняння можна повернутися до множинної нелінійної регресії: α = eβ0 , D = αPβ1 M β2 .
Перевірку на адекватність здійснюємо аналогічно до моделі множинної лінійної регресії.
Процедура зведення нелінійної регресійної моделі до лінійної шляхом логарифмування лівої та правої частин залежності називається лінеаризацією.
Типове завдання
1.За допомогою процедури Regression надбудови Data Analysis побудувати функцію попиту на товар D залежно від ціни P і прибутку M у ви-
гляді D = α Pβ1 M β2 , де α , β1 , β2 — деякі числові коефіцієнти. Знайти множинний коефіцієнт детермінації. Зробити висновки щодо адекватності побудованої моделі, якщо рівень значущості α = 0,05 .
2.Виключити по черзі одну зі змінних і побудувати парні нелінійні регре-
сійні моделі вигляду D = α Pβ1 і D = α M β2 . Перевірити їх на адекватність. Яка зі всіх розглянутих адекватних регресійних моделей „найкраща”?
D (кг) P (грн) M (грн)
7,27 |
0,99 |
1747 |
10,89 |
1,37 |
1810 |
11,65 |
2,39 |
2138 |
14,80 |
2,78 |
2162 |
15,06 |
3,12 |
2306 |
16,98 |
3,21 |
2424 |
20,38 |
3,26 |
2501 |
20,79 |
3,33 |
2838 |
21,11 |
3,63 |
3029 |
22,93 |
4,30 |
3567 |
87

Хід роботи
Крок 1. Прологарифмувати всі вхідні дані, використавши вбудовану функцію LN (рис. 67).
Рис. 67. Логарифмування вхідних даних.
Крок 2. Скористатися процедурою Regression надбудови Data Analysis і у відповідному діалоговому вікні в полі Іnput Y Range ввести значення Y = ln D , а в полі Іnput X Range — водночас значення X1 = ln P та X2 = ln M . Отримаємо
(рис. 68) рівняння регресії
yˆ = −2,31+ 0,50x1 + 0,59x2 .
88
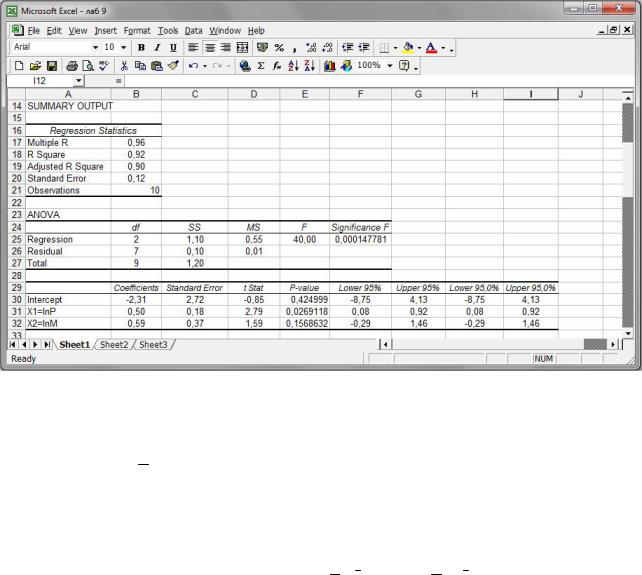
Рис. 68. Лінеаризована модель.
Це рівняння регресії неадекватне внаслідок того, що p -значення 0,1569
для коефіцієнта β2 = 0,59 перевищує заданий рівень значущості α = 0,05 , а то-
му коефіцієнт β2 регресії не значущий на рівні 0,05.
Крок 3. Виключивши по черзі одну зі змінних, побудувати парні нелінійні регресійні моделі вигляду D = α Pβ1 та D = α M β2 (рис. 69 і 70).
89
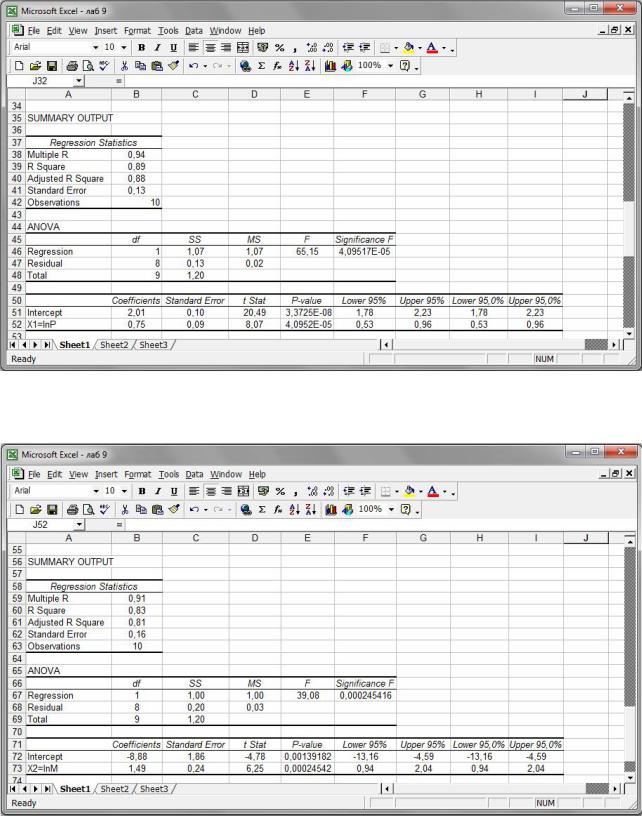
Рис. 68. Виключення з розгляду змінної X2 = ln M .
Рис. 69. Виключення з розгляду змінної X1 = ln P .
На цьому кроці отримаємо лінеаризовані регресійні моделі yˆ = 2,01+ 0,75x1 та yˆ = −8,88 +1,49x2 ,
90
