
Вказівки до лаб_2010
.pdf
4. Знайти ймовірності потрапляння ознаки генеральної сукупності (випадкової величини) ξ у проміжки (−∞; z1] , (z1; z2 ], (z2; z3 ], ..., (zl−1; + ∞) :
p1 = P{ξ Î(-¥; z1]} = Fξ (z1 ) - Fξ (-¥) = Fξ (z1 ) - 0 = Fξ (z1 ), p2 = P{ξ Î(z1; z2 ]} = Fξ (z2 ) - Fξ (z1 ) ,
p3 = P{ξ Î(z2; z3 ]} = Fξ (z3 ) - Fξ (z2 ),
.............................................................,
pl−1 = P{ξ Î(zl−2; zl−1]} = Fξ (zl−1 ) - Fξ (zl−2 ) ,
pl = P{ξ Î(zl−1; + ¥)} = Fξ (+¥) - Fξ (zl−1 ) =1- Fξ (zl−1 ) ,
де Fξ (z1 ) , Fξ (z2 ), ..., Fξ (zl−1 ) — значення функції розподілу
F |
(x) = 1 |
+ F |
æ x - x ö |
||||
ç |
|
|
|
÷ |
|||
ξ |
|
|
|
|
|||
|
2 |
|
è |
σ |
ø |
||
для випадкової величини ξ , розподіленої за нормальним законом з параме-
трами a = x та σ = σ , Φ(x) — значення функції Лапласа. Особливу увагу тут потрібно звернути на знаходження ймовірностей p1 та pl .
5.Обчислити теоретичні частоти ni′ = n × pi (i =1,l ), де n — об’єм заданої
вибірки. Прослідкувати за тим, щоб виконувались наступні умови:
а) у випадку, коли 50 £ n < 200, перша та остання теоретичні частоти n1′ і nl′ повинні бути не меншими за 1, а всі решта частоти n′2 , ..., nl′−1 — не меншими за 5;
б) якщо обсяг вибірки n ³ 200, то достатньо, щоб усі теоретичні частоти ni′ (i =1, 2, ..., l ) були не меншими за 5.
При порушенні цих умов провести об’єднання таких інтервалів (інтервалів з малими теоретичними частотами ni′ ) разом із сусідніми інтерва-
лами, причому відповідні емпіричні ( ni ) та теоретичні ( ni′ ) частоти дода-
ються, а загальна кількість інтервалів при цьому зменшується.
6.Обчислити спостережуване значення критерію χ 2 за формулою
51

|
l |
(ni − ni′) |
2 |
χспост2 |
. = å |
|
|
|
i=1 |
ni′ |
|
та порівняти його з критичним значенням χкр2 . = χα2; k розподілу χ 2 для за-
даного в умові рівня значущості α та k = l − 3 ступенів вільності, де l — кількість нових, уже об’єднаних інтервалів.
7.Прийняти рішення:
∙якщо χспост2 . < χкр2 . , то для рівня значущості α немає підстав відхиляти гі-
потезу про те, що ознака генеральної сукупності розподілена за нормальним законом з параметрами a = x та σ = σ ;
∙якщо χспост2 . > χкр2 . , то гіпотеза про те, що ознака генеральної сукупності розподілена за нормальним законом із параметрами a = x та σ = σ , відхиляється на рівні α ;
∙якщо значення χспост2 . та χкр2 . мало відрізняються між собою, то придат-
ність критерію хі-квадрат для перевірки гіпотези про вид розподілу може ставитися під сумнів; у такому випадку краще скористатися більш потужними критеріями для перевірки гіпотези про вид розподілу (наприклад, критерієм Колмогорова).
Критерій Колмогорова
Необхідною умовою для використання критерію Колмогорова є неперервність гіпотетичного закону ознаки генеральної сукупності. У критерії Колмогорова в ролі критеріальної статистики вибирають таку, яка враховує відхи-
лення між емпіричною Fξ* (x) та теоретичною Fξ (x) функціями розподілу.
Для перевірки гіпотези про нормальність розподілу ознаки генеральної сукупності за допомогою критерію Колмогорова дотримуються наступної послідовності дій.
52

1. Знайти об’єм вибірки n , вибіркове середнє x = |
1 |
n |
|||
åxi та вибіркове серед- |
|||||
|
|
|
|
n i=1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
ньоквадратичне відхилення σ |
= |
1 å(xi - x )2 . |
|
|
|
|
|
n i=1 |
|
|
|
2.Побудувати ранжований ряд для заданої вибірки: x1′ ≤ x′2 ≤ ... ≤ x′m ≤ ... ≤ x′n
(надалі вважатимемо m =1, 2, ..., n — порядковий номер елемента вибірки
вранжованому ряді).
3.Послідовно знайти значення теоретичної функції розподілу Fξ (x) у точ-
|
′ |
′ |
|
′ |
|
|
|
|
що ознака генеральної сукупності роз- |
|||||||||||
|
ках x = x1 , |
x2 |
, ..., xn , припускаючи, |
|||||||||||||||||
|
поділена нормально з параметрами a = x |
та σ = σ |
. |
|
|
|
|
|
||||||||||||
4. |
Обчислити |
+ |
æ m |
|
¢ ö |
− |
æ |
|
¢ |
- |
m -1 |
ö |
′ |
|||||||
Dn |
= maxç |
- Fξ (xm )÷ |
, Dn |
= maxç Fξ |
(xm ) |
n |
÷, де xm — |
|||||||||||||
|
|
|
|
1≤m≤n è n |
|
ø |
|
|
1≤m≤n è |
|
|
ø |
|
|||||||
|
впорядковані елементи ранжованого ряду ( m =1, 2, ..., n ), а також знайти |
|||||||||||||||||||
|
критеріальну статистику Dn = max(Dn+ , Dn− ). |
|
|
|
|
|
||||||||||||||
5. |
При обсягу вибірки n ³10 |
та рівні значущості |
0,01≤ α ≤ 0,2 |
критичне |
||||||||||||||||
|
значення Dкр. |
можна розраховувати за наближеною формулою |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
» |
- |
ln(0,5α ) |
- |
1 |
, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
кр. |
|
|
|
|
2n |
|
|
6n |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
де α — заданий в умові рівень значущості.
6.Прийняти рішення:
·якщо Dn < Dкр. , то згідно з критерієм Колмогорова на рівні значущості
α немає жодних підстав відхиляти гіпотезу про те, що ознака генеральної сукупності розподілена за нормальним законом з параметрами a = x та σ = σ ;
· якщо ж Dn > Dкр. , то ця гіпотеза відхиляється.
53

Типовий приклад
На основі заданої вибірки для рівня значущості α = 0,05 перевірити гіпо-
тезу про нормальність розподілу ознаки генеральної сукупності, користуючись критеріями χ 2 (Пірсона) та Колмогорова.
5,4 |
9,3 |
9,4 |
5,6 |
7,8 |
7,8 |
8,7 |
7,4 |
9,4 |
6,5 |
10,1 |
11,5 |
9 |
15,8 |
9,2 |
9,7 |
15,1 |
11,8 |
10,7 |
6,3 |
12,4 |
8,1 |
20,2 |
9,3 |
15,2 |
10,5 |
15,3 |
5,4 |
10,3 |
6,3 |
8,4 |
9,9 |
5,3 |
11,1 |
7,9 |
10,4 |
10,8 |
12,2 |
10,5 |
6,1 |
13,2 |
9,9 |
13,2 |
12,7 |
11,9 |
9,1 |
9,8 |
8,8 |
14,5 |
7,3 |
Зробити належні висновки.
Хід роботи Критерій χ 2 (Пірсона)
Крок 1. Записати вибірку у вигляді одного стовпця та побудувати ранжований ряд, впорядкувавши елементи вибірки від найменшого до найбільшого, а також знайти об’єм вибірки n , вибіркове середнє x (наприклад, за допомогою функції AVERAGE) та вибіркове середньоквадратичне відхилення σ (STDEVP). Знайти найбільший та найменший елементи, розмах вибірки, кількість інтервалів за формулою Стерджеса та побудувати таблицю інтервальних частот (див. кроки 1–4 лаб. роботи № 3) — рис. 41.
54
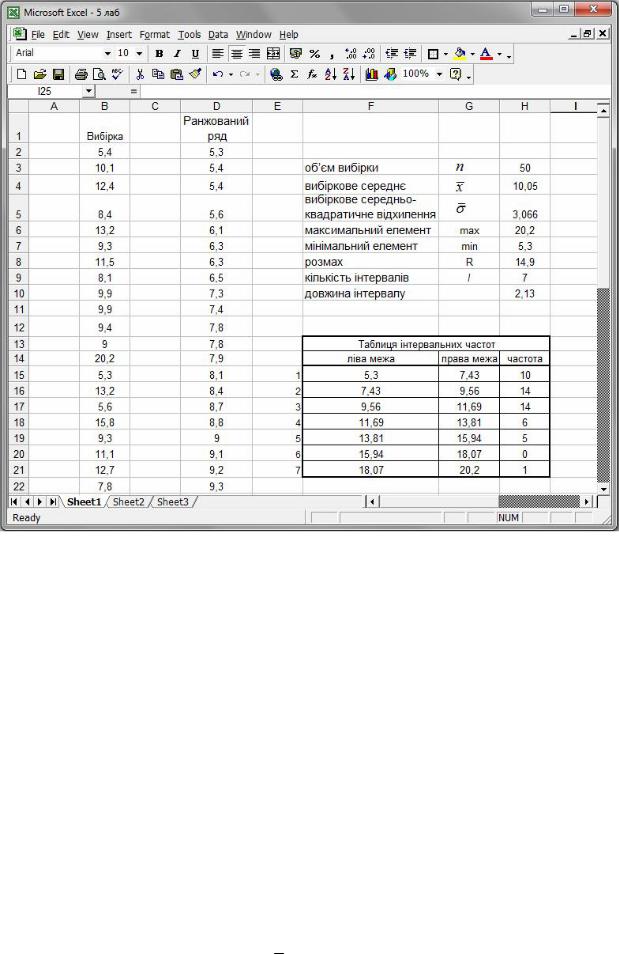
Рис. 41. Таблиця інтервальних частот.
Крок 2. У побудованій таблиці інтервальних частот замінити ліву межу z0 першого інтервалу [z0; z1] на −∞ , а праву межу zl останнього інтервалу
(zl−1; zl ] — на +∞ . Далі знайти значення теоретичної функції розподілу Fξ (zi )
(для нормального закону розподілу) в кожній з точок zi розбиття на інтервали, пам’ятаючи, що Fξ (−∞) = 0 , а Fξ (+∞) =1.
Зауваження 4. Значення функції розподілу Fξ (zi ) (для нормального за-
кону розподілу) у точках zi (i =1, 2, ..., l −1) можна знайти в Excel, користую-
чись функцією NORMDIST. Аргументами функції NORMDIST є: Х — точка zi ,
Mean — розраховане нами вибіркове середнє x ,
Standard_dev — значення σ ,
55

Cumulative — стала 1 (оскільки шукаємо значення функції розподілу в точці, а не густини розподілу).
Крок 3. Обчислити гіпотетичні ймовірності pi = Fξ (zi ) − Fξ (zi−1 ), i =1, 2, ..., l , не забуваючи про те, що Fξ (−∞) = 0 , а Fξ (+∞) =1, а також теоре-
тичні частоти ni′ за формулою ni′ = n × pi (рис. 42).
Рис. 42. Розрахунок теоретичних частот ni′ для критерію хі-квадрат.
Крок 4. Оскільки об’єм вибірки 50 ≤ n < 200, то переконатися в тому, що всі теоретичні частоти ni′ (за винятком крайніх) не менші за 5; крайні ж частоти повинні бути не меншими за 1.
У нашому випадку n7′ = 0,22 <1, тому останній, сьомий, інтервал
(18,07; + ∞) потрібно об’єднати з попереднім (15,94;18,07] , — отримаємо про-
міжок (15,94; + ∞), якому відповідатимуть теоретична частота
56

n6′ = 0,22 +1,14 = 1,36 і, відповідно, емпірична частота n6 = 0 +1= 1. Після такого
об’єднання кількість інтервалів розбиття зменшується до шести: |
l = 6, n6 =1, |
n6′ =1,36 . |
|
Проте, після такого об’єднання серед теоретичних частот ni′ |
залишається |
одна, менша за 5: n5′ = 4,12. Тому проміжок (13,81;15,94] потрібно об’єднати із сусіднім “зверху” або “знизу”. Об’єднаємо (13,81;15,94] , наприклад, з останнім інтервалом (15,94; + ∞) і отримаємо тепер уже l = 5 інтервалів розбиття, при-
чому останній інтервал матиме вигляд (13,81; + ∞) , а n5 = 5 +1= 6; n5′ = 4,12 +1,36 = 5,48 (рис. 43).
Рис. 43. Об’єднання інтервалів із малими теоретичними частотами.
57

Крок 5. Обчислити спостережуване значення статистики хі-квадрат за
|
l |
(ni − ni′) |
2 |
формулою χспост2 |
. = å |
(рис. 44) та порівняти його з критичним значен- |
|
|
i=1 |
ni′ |
|
ням χкр2 . = χα2; k , яке розрахувати за допомогою функції CHIINV. Аргументами
функції CHIINV є:
Probability — заданий в умові рівень значущості α ;
Deg_freedom — кількість ступенів вільності k = l − 3, де l — кількість інтервалів після об’єднання.
Крок 6. Зробити висновки.
Рис. 44. Розрахунок спостережуваного та критичного значень для критерію хі-квадрат.
Критерій Колмогорова
Крок 1. Записати вибірку у вигляді одного стовпця та побудувати ранжований ряд, впорядкувавши елементи вибірки від найменшого до найбільшого, а також знайти об’єм вибірки n , вибіркове середнє x (наприклад, за допомогою функції AVERAGE) та вибіркове середньоквадратичне відхилення σ (STDEVP). Поставити у відповідність кожному елементу ( x′m ) ранжованого ря-
ду його порядковий номер m (m =1, 2, ..., n ) (рис. 45).
58
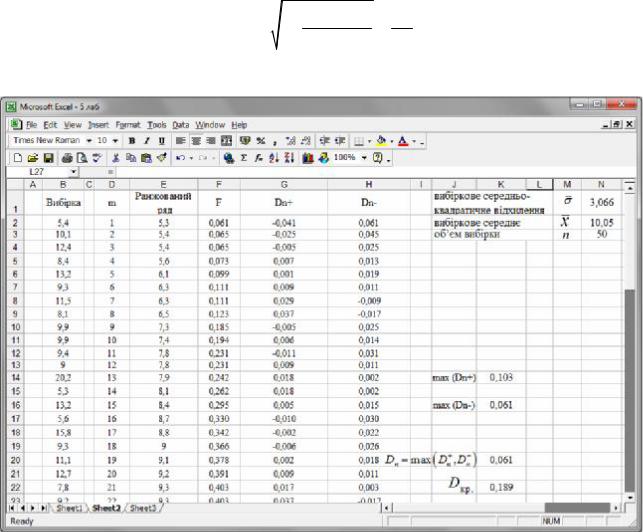
Крок 2. Обчислити значення функції розподілу (для нормального закону розподілу) Fξ (x′m ) в кожній із точок x′m (m =1, 2, ..., n ), користуючись функці-
єю NORMDIST (рис. 45).
+ |
æ m |
¢ |
ö |
− |
æ |
¢ |
m -1ö |
, а |
Крок 3. Обчислити Dn |
= maxç |
- Fξ (xm )÷ |
, Dn |
= maxç Fξ (xm ) - |
÷ |
|||
|
1≤m≤n è n |
|
ø |
|
1≤m≤n è |
|
n ø |
|
також критеріальну статистику Dn = max(Dn+ , Dn− ) і критичне значення
» - ln(0,5α ) - 1
Dкр. 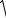 2n 6n ,
2n 6n ,
де α — заданий в умові рівень значущості (рис. 45).
Рис. 45. Розрахунок спостережуваного та критичного значень для критерію Колмогорова.
Крок 4. Зробити належні висновки.
Висновок. Після об’єднання інтервалів із „малими” теоретичними частотами ni′ для критерію хі-квадрат
χспост2 . =1,62 < 5,99 = χкр2 . = χ0,05;2 2.
59

Для критерію Колмогорова
Dn = 0,10 < 0,19 = Dкр..
Незважаючи на те, що критерій Колмогорова потужніший за критерій хіквадрат, на основі обидвох критеріїв можна зробити висновок: для рівня значущості α = 0,05 немає підстав відхиляти гіпотезу про те, що ознака генераль-
ної сукупності має нормальний закон розподілу з параметрами a = 10,05;
σ = 3,07 .
Лабораторна робота № 6-7
Парна лінійна та нелінійна регресії
Основні поняття
Нехай ξ та η — деякі ознаки генеральної сукупності. Двовимірною ви-
біркою обсягу (об’єму) n називатимемо сукупність n впорядкованих пар чисел (x1, y1 ), (x2 , y2 ), ..., (xn , yn ), причому значення xi (i =1,n) — незалежні реаліза-
ції випадкової величини ξ , а yi (i =1,n) — незалежні реалізації випадкової ве-
личини η .
Двовимірну вибірку можна зобразити графічно шляхом нанесення на ко-
ординатну площину точок (xi , yi ) (i =1,n). Отриману таким чином точкову діаграму називають діаграмою розсіювання або кореляційним полем.
Кажуть, що між ознаками генеральної сукупності ξ та η простежується
кореляційний зв’язок, якщо зміна однієї випадкової величини призводить до зміни середнього значення (тобто математичного сподівання) іншої.
Метою кореляційного аналізу є оцінка щільності кореляційного зв’язку між ознаками генеральної сукупності.
Метою регресійного аналізу є встановлення аналітичної форми кореляційного зв’язку між ознаками генеральної сукупності.
60
