
Вказівки до лаб_2010
.pdf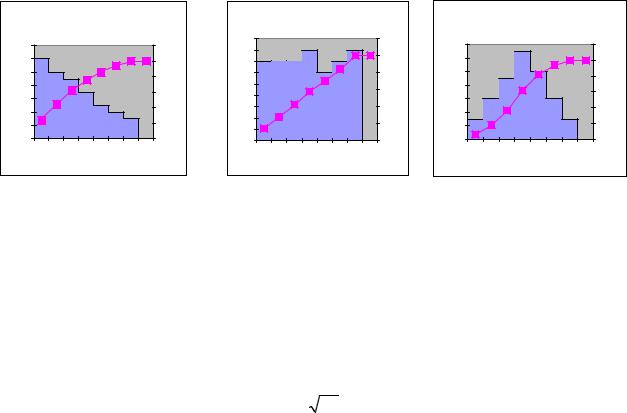
Неважко переконатись у тому, що сума всіх інтервальних частот у побу-
дованій таблиці дорівнює об’єму вибірки n . |
|
|
|
|
|
|
||
Для |
неперервної вибірки |
графік емпіричної |
функції розподілу |
F (x) |
||||
|
|
|
|
|
|
|
|
ξ |
|
через точки (zi ;ω (zi |
)) , де ω (zi ) = |
1 |
i |
|
1 |
(n1 + n2 +L + ni ) |
|
проходить |
ånj = |
— на- |
||||||
|
|
|
n |
j=1 |
|
n |
|
|
копичені відносні частоти. Зауважимо, що емпірична функція розподілу — завжди неспадна.
Гістограма частот — це східчаста фігура, складена з прямокутників,
основами яких є інтервали (zi−1; zi ], а їх висоти hi = |
ni |
(i = |
|
). Зауважимо, що |
|
1,l |
|||||
z |
|||||
|
|
|
|
площа гістограми частот дорівнює об’єму вибірки.
Побудова гістограми при аналізі статистичних даних відіграє дуже велику роль, оскільки за зовнішнім виглядом гістограми можна робити висновок про закон розподілу ознаки генеральної сукупності. На рис. 27 а-в зображено типові приклади гістограм залежно від гіпотетичного закону розподілу та графіки відповідних емпіричних функцій розподілу.
|
|
|
Histogram |
|
|
|||
|
14 |
|
|
|
|
|
|
120,00% |
|
12 |
|
|
|
|
|
|
100,00% |
Frequency |
10 |
|
|
|
|
|
|
80,00% |
8 |
|
|
|
|
|
|
||
|
|
|
|
|
|
60,00% |
||
6 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
40,00% |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
20,00% |
|
0 |
|
|
|
|
|
|
,00% |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
More |
|
|
|
|
Bin |
|
|
|
|
|
а) показниковий |
|||||||
|
(експоненційний) |
|||||||
|
|
|
Histogram |
|
|
|
|
9 |
|
|
|
|
|
|
120,00% |
8 |
|
|
|
|
|
|
100,00% |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
80,00% |
5 |
|
|
|
|
|
|
60,00% |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Frequency |
|
|
|
|
|
|
40,00% |
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
20,00% |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
,00% |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
More |
|
|
|
|
Bin |
|
|
|
|
б) рівномірний |
||||||
|
|
Histogram |
|
|
14 |
120,00% |
|
|
12 |
100,00% |
|
Frequency |
10 |
80,00% |
|
8 |
|||
60,00% |
|||
6 |
|||
40,00% |
|||
4 |
|||
|
|
||
|
2 |
20,00% |
|
|
0 |
,00% |
|
|
6,6 |
8,04 9,4810,9212,3613,815,24More |
|
|
|
Bin |
|
|
|
в) нормальний |
Рис. 27. Типові приклади гістограм залежно від виду розподілу
Нагадаємо, що випадкова величина ξ називається нормально розподіле-
ною з параметрами a та σ , якщо її густина розподілу може бути записана у вигляді
fξ (x) = |
1 |
|
|
− |
(x−a)2 |
|
|
×e |
2σ 2 |
||||
|
|
|
|
|
||
σ 2π |
|
|
||||
|
|
|
|
|
||
31

При a = 0 та σ = 1 нормальний розподіл перетворюється на стандартний нормальний розподіл. Для стандартного нормального розподілу
x2
fξ (x) = 1π ×e − 2 = ϕ (x) — функція Гаусса,
 2
2
F (x) = |
1 × ò e − |
x2 |
1 + F(x), |
|||
2 dx = |
||||||
ξ |
|
|
x |
|
|
|
|
|
|
|
|
|
|
2π − ∞ |
|
|
2 |
|||
|
|
|
|
|||
де F(x) — функція Лапласа.
Для випадкової величини ξ , яка має нормальний закон розподілу з пара-
метрами a та σ , математичне сподівання Mξ = a , дисперсія Dξ = σ 2 .
Моду та медіану для неперервної вибірки обчислюють наступним чином. Якщо неперервна вибірка задається таблицею інтервальних частот з рів-
новеликими інтервалами довжини z , то її мода визначається за формулою
Mo = zi−1 + Dz × 2ni - ni−1 - ni+1
де zi−1 — нижня межа модального інтервалу (того, що містить максимальну кі-
лькість елементів), ni — число елементів вибірки в цьому інтервалі (модальна частота), ni−1 , ni+1 — число елементів вибірки в сусідніх до модального інтерва-
лах (передмодальному та післямодальному інтервалах відповідно).
Медіаною вибірки (позначатимемо її Me ) називається таке значення x , в
якому емпірична функція розподілу набуває значення 0,5: Fξ* (Me) = 0,5 . У ви-
падку, коли вибірка — неперервна і задана таблицею інтервальних частот з рівновеликими інтервалами довжини z , то медіану цієї вибірки можна обчислити за формулою
Me = zi−1 + Dz × n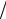 2 - (n1 + n2 +K+ ni−1 ) , ni
2 - (n1 + n2 +K+ ni−1 ) , ni
де zi−1 — нижня межа медіанного інтервалу (інтервал, для якого накопичена ча-
стота дорівнює півсумі всіх частот або вперше перевищить її), ni — число еле-
ментів вибірки, які потрапили в цей інтервал, (n1 + n2 +K+ ni−1 ) — сумарне чи-
сло елементів вибірки в інтервалах, які лежать зліва від медіанного.
32
Типовий приклад
У таблиці наведено час обслуговування (у хв.) 30 навмання відібраних протягом дня клієнтів банківської установи:
8,61 |
9,25 |
9,23 |
10,00 |
7,95 |
8,48 |
9,66 |
10,44 |
8,90 |
9,12 |
7,86 |
11,12 |
7,42 |
9,54 |
7,35 |
8,27 |
11,39 |
7,42 |
8,55 |
9,92 |
12,36 |
8,04 |
7,22 |
11,69 |
6,43 |
7,42 |
10,16 |
5,16 |
9,01 |
10,72 |
Для заданої неперервної вибірки побудувати таблицю інтервальних частот, використовуючи формулу Стерджеса, та гістограму частот. Побудувати графік емпіричної функції розподілу.
Порівняти гіпотетичний розподіл генеральної сукупності з нормальним. Обчислити моду та медіану заданої вибірки.
Дати інтерпретацію отриманих результатів.
Хід роботи
Крок 1. Зобразити вибірку у вигляді одного стовпця, побудувати для неї ранжований ряд, знайти об’єм вибірки, мінімальний та максимальний елементи, розмах вибірки (див. кроки 1, 2 і 9 лабораторної роботи №2).
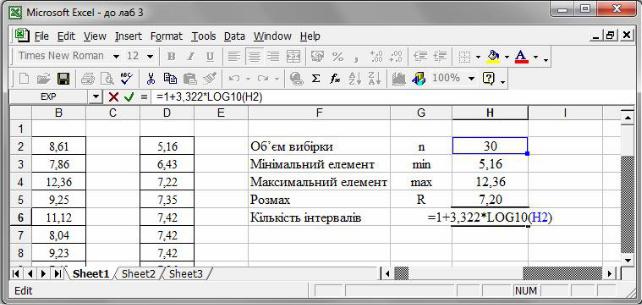
Крок 2. Знайти кількість інтервалів розбиття за формулою Стерджеса (рис. 28) і заокруглити результат до цілих за допомогою функції ROUND (рис. 29).
Рис. 28. Знаходження кількості інтервалів за формулою Стерджеса.
33

Аргументами функції ROUND є:
Number — число, яке необхідно округлити;
Num_digits — кількість десяткових знаків після коми (рис. 29).
Рис. 29. Процедура заокруглення. |
|
||
Крок 3. Розрахувати довжину кожного інтервалу за формулою z = |
b − a |
, |
|
l |
|||
|
|
||
вважаючи, що b = xmax , a = xmin , а l — кількість інтервалів, округлена до цілих.
Крок 4. Розбити вибірку на інтервали і зазначити кількість елементів вибірки, які потрапили в кожний інтервал (рис. 30). Отримаємо таким чином таблицю інтервальних частот.
34

Рис. 30. Таблиця інтервальних частот.
Крок 5. Побудувати гістограму та графік емпіричної функції розподілу
Fξ* (x) за допомогою процедури Data Analysis → Histogram. У відповідному діалоговому вікні (рис. 31) зазначити:
–у полі Input Range вводимо стовбець елементів вибірки;
–у полі Bin Range — праві межі інтервалів розбиття;
–у полі Output Range — результуючу клітинку;
–мітки біля Cumulative Percentage i Chart Output.
35
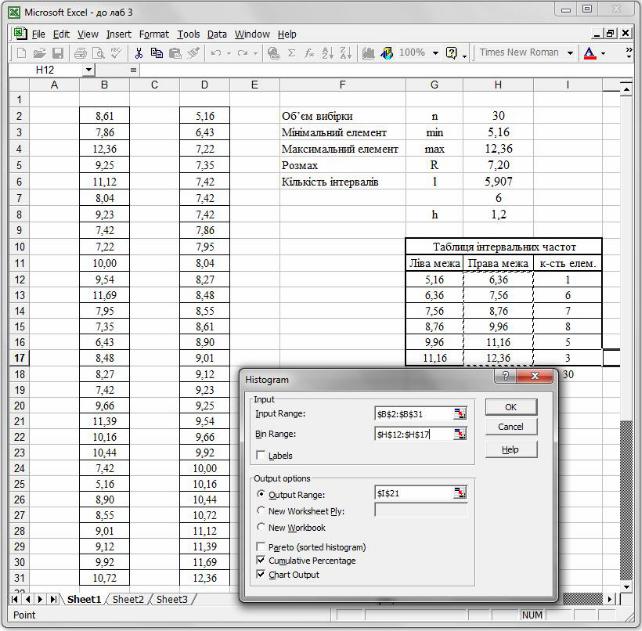
Рис. 31. Побудова гістограми.
На рис. 32 зображено гістограму (стовпчикову діаграму) і (рожевим кольором) графік емпіричної функції розподілу.
Крок 6. Звертаємо увагу на те, що на гістограмі, побудованій за допомогою Data Analysis, числові підписи під віссю абсцис дещо зміщені вліво, а на осі ординат відкладено інтервальні частоти, які необхідно скоригувати, поділивши їх на z (рис. 32). Відповідні зміни потрібно зробити і у полі Values на вкладці Series, яку можна викликати шляхом натискання правою кнопкою миші по вікну гістограми і вибору контекстного меню Source Data (у полі Values вказати скориговані інтервальні частоти, рис. 33, 34).
36
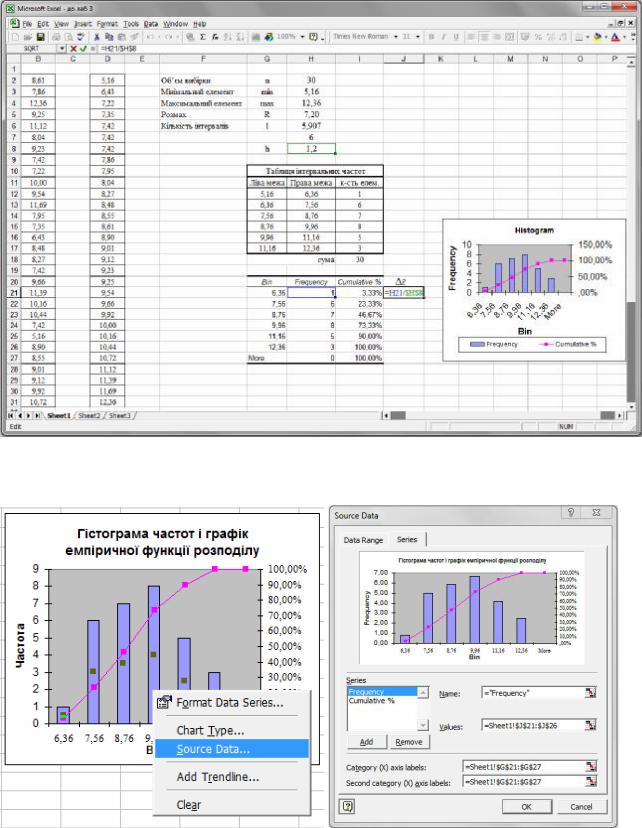
Рис. 32. Ділимо висоту кожного прямокутника на z .
Рис. 33. Контекстне меню Source Data |
Рис. 34. Вкладка Series контекстного |
для гістограми |
меню Sourсe Data для гістограми. |
Крок 7. За зовнішнім виглядом отриманої гістограми (рис. 35) зробити висновки щодо наближення розподілу генеральної сукупності до нормального.
37
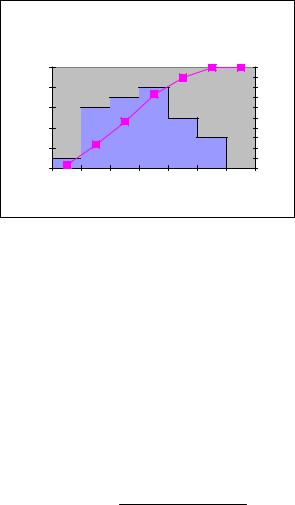
Гістограма частот і графік емпіричної функції розподілу
|
10 |
|
|
|
|
|
100,00% |
|
8 |
|
|
|
|
|
90,00% |
|
|
|
|
|
|
80,00% |
|
Частота |
6 |
|
|
|
|
|
70,00% |
|
|
|
|
|
60,00% |
||
4 |
|
|
|
|
|
50,00% |
|
|
|
|
|
|
40,00% |
||
|
|
|
|
|
|
30,00% |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
20,00% |
|
|
0 |
|
|
|
|
|
10,00% |
|
|
|
|
|
|
,00% |
|
|
6,36 |
7,56 |
8,76 |
9,96 |
11,16 |
12,36 |
More |
|
|
|
інтервали |
|
|
||
Рис. 35. Гістограма частот і графік емпіричної функції розподілу.
Крок 8. Обчислити моду та медіану вибірки.
Матимемо: модальний інтервал: (8,76; 9,96], модальна частота ni = 8 ; крім того, ni−1 = 7 , ni+1 = 5 . Тоді:
Mo = 8,76 +1,2 × |
8 - 7 |
= 9,06 . |
2×8 - 7 - 5 |
Медіанний інтервал — також (8,76; 9,96], n = 30 — об’єм вибірки. Тоді:
Me = 8,76 +1,2 × 30 2 - (1+ 6 + 7) = 8,91. 8
2 - (1+ 6 + 7) = 8,91. 8
Отже, для половини клієнтів банківської установи час обслуговування менший за 8,91 хв., а для іншої половини — більший, ніж 8,91 хв.
Висновок.
У даній лабораторній роботі ми досліджували вибірку з 30 елементів, кожен з яких — це час обслуговування (у хв.) клієнтів у банківській установі.
Так, для першого клієнта час обслуговування становить 8,61 хв., для другого — 7,86 хв., для третього — 12,36 хв. і т.д.
Проведені дослідження показують, що найменший час обслуговування клієнтів — 5,16 хв., а найбільший — 12,36 хв.
Ми побудували таблицю інтервальних частот, розбивши діапазон елементів вибірки на 6 інтервалів (кількість інтервалів знайдено за формулою Стерджеса, довжина кожного інтервалу z =1,2 хв.). Із цієї таблиці видно, що в бан-
38
ківській установі лише для одного клієнта час обслуговування — від 5,16 хв. до 6,36 хв. включно; для 6 клієнтів — від 6,36 хв. до 7,56 хв. включно і т.д.
Неважко помітити , що в таблиці інтервальні частоти спочатку поступово збільшуються, потім — поступово зменшуються, що свідчить про наближення розподілу в генеральній сукупності до нормального. Побудована гістограма також підтверджує той факт, що ознака генеральної сукупності має приблизно нормальний закон розподілу.
Обчислено моду і медіану. Значення медіани 8,91 показує, що для половини клієнтів банківської установи час обслуговування менший за 8,91 хв., а для іншої половини — більший, ніж 8,91 хв.
Лабораторна робота № 4
Точкові та інтервальні оцінки параметрів розподілу
Основні поняття
Нехай ξ — ознака генеральної сукупності; x1 , x2 , ..., xn — задана вибір-
ка. Як відомо, кожна випадкова величина має свій закон розподілу, який у більшості випадків залежить від певних параметрів, наприклад: нормальний закон розподілу повністю визначається двома параметрами — a та σ , показниковий або пуассонівський — одним параметром λ , рівномірний — параметрами a та b (ліва та права межі інтервалу) і т. д. У випадку дослідження вибірки параметри гіпотетичного розподілу генеральної сукупності залишаються невідомими, тому перед нами постає завдання оцінити ці параметри, тобто знайти їх наближені значення.
Завдяки вибірковому методу можна знайти наближені значення невідомих параметрів при виконанні ряду умов.
Точковою оцінкою θ* невідомого параметра θ називається будь-яка фун-
кція f (x1, x2 ,K, xn ) елементів вибірки.
39

На практиці серед точкових оцінок невідомого параметра θ намагаються вибрати лише такі, що задовольняють умови незміщеності, змістовності та ефективності.
Точкова оцінка θ* називається незміщеною точковою оцінкою параме-
тра θ, якщо M (θ* ) = θ, тобто математичне сподівання θ* дорівнює оцінювано-
му параметру θ незалежно від об’єму вибірки.
Змістовною (обґрунтованою) називають точкову оцінку θ* , дисперсія якої при необмеженому зростанні об’єму вибірки (n → ∞) прямує за ймовірніс-
тю до нуля: P{Dθ = 0} →1 при n → ∞ .
Ефективною називають точкову оцінку θ* , яка при заданому об’ємі вибірки має найменшу можливу дисперсію у класі незміщених лінійних оцінок параметра θ.
Оскільки основними числовими характеристиками випадкової величини ξ є математичне сподівання Mξ та дисперсія Dξ , і вони у переважній більшо-
сті випадків виражаються через невідомі параметри розподілу, то проблеми знаходження точкових оцінок для невідомих параметрів розподілу і точкових оцінок для математичного сподівання і дисперсії тісно пов’язані між собою.
Розглянемо основні числові характеристики вибірки.
1.Вибіркове середнє x є точковою оцінкою для математичного сподівання генеральної сукупності: x ≈ Mξ . У випадку, коли ознака ξ має нормальний закон розподілу, то вибіркове середнє є незміщеною, змістовною і навіть ефективною точковою оцінкою математичного сподівання.
2.Вибіркова дисперсія D — змістовна, але зміщена, точкова оцінка дисперсії
генеральної сукупності.
%
3. Виправлена вибіркова дисперсія D — змістовна і незміщена точкова оцін-
% ≈ ξ
ка дисперсії генеральної сукупності: D D .
4.Вибіркове середньоквадратичне відхилення σ .
5.Виправлене вибіркове середньоквадратичне відхилення σ%.
40
