109

Приложения

1. Использование математических методов в теории систем

1.1. Математическое описание систем

Определение 1. Системой называется отношение на непустых множествах:

где ×- символ декартова произведения; I – множество индексов; Vi – элемент

Y × {Vi : i IY } - выходным элементом системы. Тогда S X ×Y . Такая система

называется системой “вход - выход”. Если S является функцией, то соответствующая система называется функциональной.

Определение 2 (для системы с конечным числом состояний). Система определяется в виде кортежа (упорядоченного набора элементов):

функция выхода.

Таким образом, система определяется в терминах ее наблюдаемых свойств или в терминах взаимосвязей между ними, а не тем, что они на самом деле собой представляют, т.е. не с помощью физических, биологических и других явлений. Это отражает суть системного подхода, направленного на выяснение организации и взаимосвязей элементов систем, а не конкретных механизмов в рамках окружающей действительности.

1.2. Методы изучения структуры систем

1.2.1. Топологический анализ. Для изучения структуры взаимосвязей элементов системы используется так называемый топологический анализ, или анализ связности, оперирующий понятиями комплекса, симплекса; q – связности и экцентрисета. Этот анализ определяет связность подсистем в системе.

Симплициальный комплекс – обобщение понятия планарного графа, отражающее многомерную природу рассматриваемого бинарного отношения между элементами системы. В общем виде систему можно представить в виде множества пар элементов, связанных некоторым отношением R. Тип отношения может быть различным: соответствие, подобие, сходство, различие и т.п.:

S = {(x, y) : x X , y Y , xRy}.

110

Отношение R порождает множество многомерных связей между элементами. Анализировать можно как связи элементов множества X,так и связи элементов множества Y. Любой элемент множества X (или Y) со связями называется симплексом. Объединение симплексов образует комплекс. Обозначение симплекса σ X (Y , R) или

σY (X , R) . Обозначение комплекса K X (Y , R) или KY (X , R) .

Задача изучения структуры связности комплекса K сводится к построению классов q-эквивалентности. Для каждого значения размерности q= 0, 1, … ,dim K (где dim K – максимальная размерность комплекса) можно определить число различных классов эквивалентности θq. Назовем эту операцию q-анализом комплекса K, а вектор θ = (θdim K , ... ,θ1 , θ0 ) - первым структурным вектором комплекса.

Симплекс σY (X , R) называется q-мерным (связным), если он содержит не менее

q+1 элементов, удовлетворяющих отношению R (число единиц в соответствующей симплексу строке матрицы инциденций). Если два симплекса q-связны, то они также q- 1, q-2, … ,0-связны в комплексе K.

Рассмотрим сущность топологического анализа на двух примерах.

Первый пример касается системы, описывающей сферу обслуживания. Пусть множество X = (хлеб, молоко, марки, обувь) представляет интересующие нас товары, а множество Y = (гастроном, универмаг, банк, почта) – предприятия сферы обслуживания, Зададим отношение R X ×Y , связывающее эти два множества: товар x j можно получить на предприятии yi . Определим систему:

S = {( y1 , x1 ),( y1 , x2 ),( y2 , x4 ),( y4 , x3 )}; для каждой пары элементов системы выполняется отношение R. Матрица инциденций r отношения R имеет вид:

Геометрически комплекс может быть представлен в виде: x1 x2 x3 x4

где X – множество вершин, Y – множество симплексов. Пустой симплекс y3 не принадлежит комплексу KY (X , R) . Комплекс KY (X , R) состоит из 1-симплекса y1 и двух 0-симплексов y2 и y4. Это означает, что данная система обнаруживает очень низкий уровень связности. При рассмотрении комплекса KY можно видеть, что θ1=1

(симплекс y1); θ0=3 (несвязные (дизъюнктные) симплексы y1, y2, y4). Следовательно, θ = (1, 3) – первый структурный вектор комплекса.

111

q=1; θ0=1 {все x, за исключением x7, x10},

где q – степень связности; θq – число компонентов связности q; { } – множество симплексов, имеющих связность q.

Следует иметь в виду, что с уменьшением степени связности некоторые симплексы объединяются в один компонент. Для объединения двух симплексов необходимо, чтобы для степени связности q, они имели не менее q+1 общих связей (число единиц в одних и тех же столбцах матрицы инциденций).

Структурный вектор комплекса равен: θ = (1, 1, 2, 3, 2, 1). Таким образом, комплекс связан для больших и малых q, а для промежуточных значений связности распадается на несколько несвязных компонентов. Существование на уровне q = n более чем одного компонента означает, что существует два n-мерных симплекса (прибора), которые не являются n-связными. Введем вектор препятствия D = θ - I, где I

– единичный вектор. Компоненты вектора D являются мерой препятствия свободному обмену информацией в комплексе на каждом уровне размерности (связности). Если на каком-то уровне компонент вектора D равен 0, то препятствие отсутствует. В рассматриваемом примере препятствие на уровне q=3 (соответствующий компонент вектора D не равен 0), означает, что симплексы (приборы) x4 и x15, хотя каждый из них может измерить, по крайней мере, четыре величины, не связаны (прямо или косвенно) никакими четырьмя величинами и ,следовательно, беспрепятственный обмен

113

Рис.1. Покрытие множества X.

Элементы множества A являются подмножествами X, т.е. можно считать Ai как

бы расположенными на N+1 уровне, полагая, что элементы X расположены на N уровне. Теперь можно определить иерархию H при помощи соотношения R, задаваемого условием: {Ai , X j } R тогда и только тогда, когда X j Ai . Такое

отношение R представляется матрицей инциденций из нулей и единиц так же как отношения, задаваемые на N уровне. Эта идея может быть распространена на дополнительные уровни иерархии и связи между ними. Использование понятий покрытия, разбиения и иерархии дает дополнительные возможности формализованного представления систем при поиске решения проблем анализа и синтеза.

1.2.3. Построение разрешающих форм. Введение отношения на множестве элементов приводит к упрощениям и появлению классов эквивалентности состояний, что можно описать с помощью функции: fi :Vi →Vi' , где Vi - заданное множество

состояний переменной wi , а Vi' - упрощенное множество состояний той же

переменной. Выбираемая функция должна быть гомоморфна (взаимно-однозначна) относительно свойств исходного множества, существенных с точки зрения рассматриваемой задачи, Такая функция называется упрощающей. Разбиение исходного множества на неразличимые классы называется разрешающей формой. Разрешающие формы могут быть упорядочены по отношению уточнения, определенного на разбиениях данного множества. Такое отношение является отношением частичного порядка и образует решетку. Для двух разбиений X и Y, определенных на одном и том же множестве, будем говорить, что X является уточненным разбиением Y, если для любой группы x X существует группа y Y

такая, что x y . Тогда Y – укрупненное разбиение X. Решетка разрешающих форм на

множестве состояний называется разрешающей формой. Рассмотрим пример. Пусть переменная, описывающая образование имеет следующие состояния: e - начальное образование; h - полная средняя школа; c - вуз; g - ученая степень. Отношение порядка является очевидным e p h p c p g , т.е. существует 8 разрешающих форм,

решетка которых изображена на рис.2 в виде диаграммы Хассе. Группам в отдельных разрешающих формах можно дать отдельные названия: “cg” – вуз или ученая степень; “hc” – полная средняя школа; “eh” – не выше средней школы; “ehc” – любое образование, кроме ученой степени; “hcg” – образование выше начального.

На рис.2 стрелки указывают направление уточнения разбиения. Для упрощения исходной системы надо двигаться в обратном направлении.

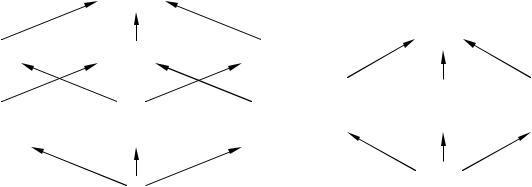
114

Для сравнения рассмотрим переменную, состояниями которой являются цвета светофора: красный, желтый, зеленый. Так как они не упорядочены, то все разбиения множества приемлемы. Соответствующая диаграмма Хассе дана на рис.3.

e-h-c-g

Без учета наименьшей уточненной формы и наибольшей число осмысленных упрощений равно λm-2.

Если имеется несколько переменных, то любая разрешающая форма для одной переменной может быть объединена с любой другой. Все эти комбинации можно включить в одну решетку, характеризующую выбор набора переменных. Она называется объединенной разрешающей формой.

Пусть X1, …, Xn – множества элементов отдельных решеток выбранных переменных, а X – множество элементов общей решетки, т.е. X = X1 × ... × X n и для

двух заданных решеток (n-ок): (x1,..., xn ) (y1,..., yn ) X мы определим ,что

(x1 , ..., xn ) ≤ ( y1 , ..., yn ) тогда, когда x j ≤ y j для всех разрешающих решеток (j = 1,

…, n). Общее число элементов объединенной разрешающей решетки равно произведению числа элементов отдельных разрешающих решеток, т.е.

115

Если все решетки одинаковы и каждая состоит из λm разрешающих форм, то

X S = (λm −1)n −1.

Если все решетки построены на полностью упорядоченном множестве с m состояниями, то

Если все переменные имеют одно и то же число разрешающих форм, например, множество X, то

Если же множества состояний еще и полностью упорядочены, и каждое состоит из m состояний, то

1.3. Аксиоматический подход к понятию сложности

Понятие сложности систем может быть определенно заданием следующих аксиом:

1. Иерархия. Если ∑i ∑, то

С(∑i)≤ С(∑), т.е. сложность подсистемы не может быть больше, чем сложность всей системы.

2. Параллельное соединение. Если ∑=∑1 … ∑k, то

С(∑) = max С(∑i),

1≤i≤k

т.е. при параллельном соединении подсистем, сложность суммарной системы определяется наиболее сложной ее частью.

3. Последовательное соединение. Если ∑=∑1 … ∑k, то

С(∑)≤С(∑1)+ … + С(∑k),

т.е. сложность системы не больше суммарной сложности подсистем. 4. Соединение с обратной связью.

C(∑1 ← ∑2)≤C(∑1)+C(∑2)+C(∑2→∑1),

где → - операция обратной связи из системы ∑2 в ∑1. 5. Нормализация.

С(∑) = 0 для всех ∑ Ω, т.е. в множестве систем ∑ существует подмножество “элементарных” систем Ω,

сложность которых равна 0.

Приведенных аксиом оказывается достаточно для определения мер сложности систем, задаваемых различными способами. Для систем с конечным числом состояний эти аксиомы однозначно определяют меру сложности, причем их количество является минимальным. Приведенные аксиомы также удобны при алгебраическом подходе к