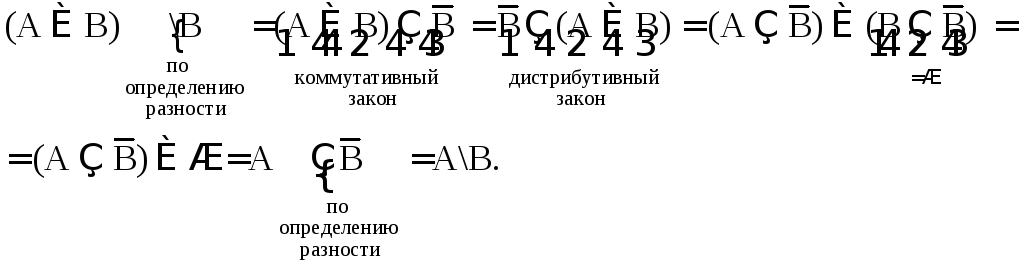- •Міністерство освіти і науки україни
- •1. Множества
- •1.1. Множество и его элементы
- •1.2. Способы задания множеств
- •1.3. Пустое множество
- •1.4. Парадокс рассела
- •1.5. Подмножества и их свойства
- •2. Операции над множествами
- •3. Основные законы алгебры множеств
- •3.1. Проверка истинности тождеств при помощи диаграмм Эйлера-Венна
- •4. Булевы операции над множествами
- •4.1. Мощность конечного множества
- •4.2. Булеан множества. Разбиение множества
- •4.3. Декартово произведение множеств. Понятие упорядоченного множества
- •4.4. Соответствия между множествами. Образ и проообраз. Бинарные соответствия
- •4.5. Способы задания бинарных соответствий
- •4.6. Типы (свойства) бинарных соответствий
- •4.7. Обратное соответствие
- •4.8. Функция
- •4.9. Отношение на множестве
- •4.10. Основные типы (свойства) бинарных отношений
- •4.11. Основные классы бинарных отношений
- •Литература
- •49600, Дніпропетровськ-5, пр. Гагаріна, 4
3. Основные законы алгебры множеств
Рассмотренные операции над множествами подчинены некоторым законам, которые напоминают известные элементарные законы алгебры чисел. Этим определяется название алгебра множеств, которую часто называют булевой алгеброй множеств, что связано с именем английского математика Джона Буля, который положил в основу своих логических исследований идею аналогии между алгеброй и логикой.
Для произвольных множеств А, В, и С справедливы следующие тождества (табл. 3.1):
Таблица 3.1
|
1. Закон тождества
| |
|
2. Коммутативность объединения
|
2’. Коммутативность пересечения
|
|
3. Ассоциативность объединения
|
3’. Ассоциативность пересечения
|
|
4. Дистрибутивность объединения относительно пересечения
|
4’. Дистрибутивность пересечения относительно объединения
|
|
5.
Законы действия с пустым
|
5’.
Законы действия с пустым
|
|
6. Закон идемпотентности объединения
|
6’. Закон идемпотентности пересечения
|
|
7. Закон де Моргана
|
7’. Закон де Моргана
|
|
8. Закон элиминации (поглощения)
|
8’. Закон элиминации (поглощения)
|
|
9. Закон склеивания
|
9’. Закон склеивания
|
|
10. Закон Порецкого
|
10’. Закон Порецкого
|
|
11. Закон инволюции (двойного дополнения)
| |
Законы
алгебры множеств по отношению к операциям
пересечения ()
и объединения ()
подчинены принципу двойственности:
если в каком-либо законе все знаки
пересечения заменить знаками объединения,
а все знаки объединения – знаками
пересечения, знак универсума (U)
заменить знаком пустого множества (Ø),
а знак пустого – знаком универсума, то
получим снова верное тождество. Например
(в силу этого принципа), из ![]() следует
следует ![]() и т. п.
и т. п.
3.1. Проверка истинности тождеств при помощи диаграмм Эйлера-Венна
Все законы алгебры множеств можно наглядно представить и доказать, используя диаграммы Эйлера-Венна. Для этого необходимо:
Начертить соответствующую диаграмму и заштриховать все множества, стоящие в левой части равенства.
Начертить другую диаграмму и сделать то же для правой части равенства.
Данное тождество истинно тогда и только тогда, когда на обеих диаграммах заштрихована одна и та же область.
Замечание 3.1. Два пересекающихся круга делят всё универсальное множество на четыре области (см. рис.3.1)
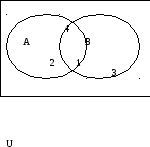
А В;
А
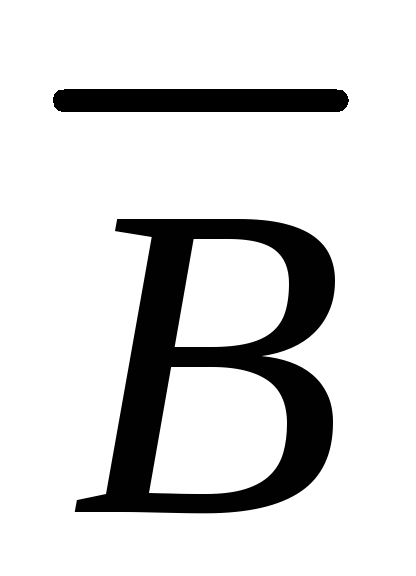 ;
; В;
В;
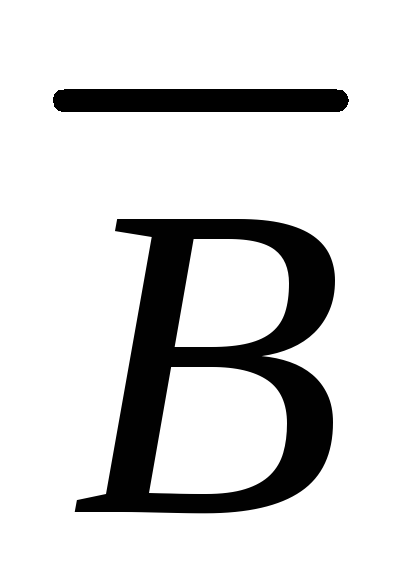 .
.
Рис.3.1
Замечание 3.2. Три пересекающихся круга делят всё универсальное множество на восемь областей (см. рис.3.2):
А В С;
А
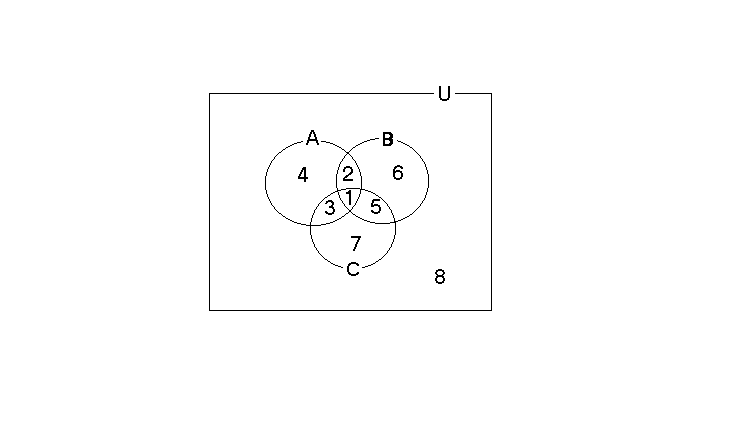
В
В
 ;
;А

С;
С;А

 ;
;
Рис.3.2
В С; В
В
 ;
;
 С;
С;

 .
.
Замечание 3.2. При записи условий различных примеров часто используются обозначения:
- из … следует…;
- тогда и только тогда, когда… .
Задача 3.1. Упростить выражения алгебры множеств:
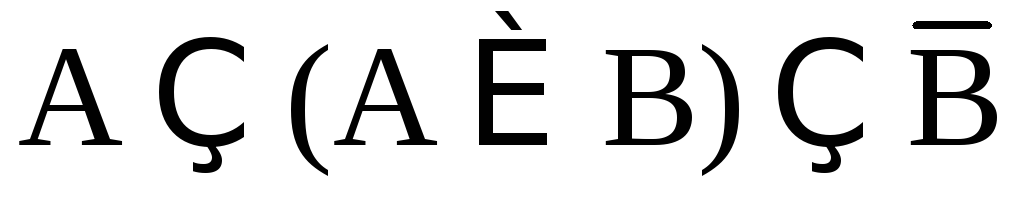 ;
;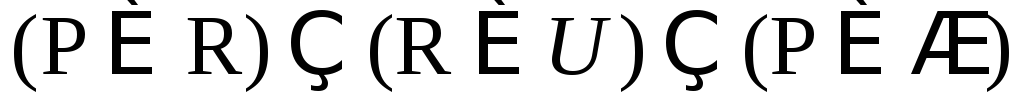 ;
;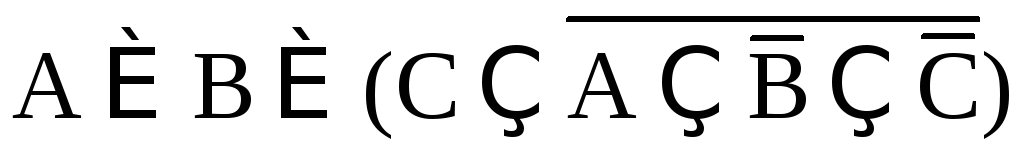 .
.
Решение.
 ;
;

Задача 3.2. Доказать тождества:
(АВ)\В = А\В;
А(ВС) = А\(А\В)(А\С).
Решение.

Задача 3.3. Доказать следующие соотношения двумя способами: с помощью диаграмм и с помощью определения равенства множеств.

A(BC) = (AB)(AC);
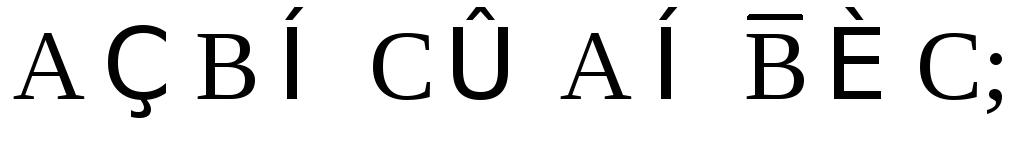

Решение.
1. Доказательство с помощью диаграммы:
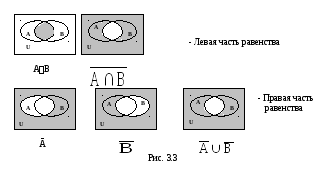
2. Доказательство с помощью определения равенства множеств.
По определению, множества Х и Y равны, если одновременно выполнены соотношения: XY и YX.
Сначала
покажем, что
![]() .
Пустьх
– произвольный элемент множества
.
Пустьх
– произвольный элемент множества
![]() ,
то естьх
,
то естьх![]() .
Это означает, чтохU
и х
.
Это означает, чтохU
и х![]() .
Отсюда вытекает, чтохА
или хВ.
Если хА,
то тогда хĀ,
а значит,
.
Отсюда вытекает, чтохА
или хВ.
Если хА,
то тогда хĀ,
а значит,
![]() .
Если жехВ,
то
.
Если жехВ,
то
![]() ,
а значит,
,
а значит,![]() .
Таким образом, всякий элемент множества
.
.
Таким образом, всякий элемент множества
.![]() .
есть также элементом множества
.
есть также элементом множества![]() То есть
То есть![]()
Теперь
докажем обратное, то есть, что
![]() .
Пусть
.
Пусть![]() .
ЕслихĀ,
то хU
и хА,
а значит, хАВ.
Отсюда следует, что
.
ЕслихĀ,
то хU
и хА,
а значит, хАВ.
Отсюда следует, что
![]() .
Если же
.
Если же![]() ,
тохU
и хВ.
Значит, хАВ,
то есть
,
тохU
и хВ.
Значит, хАВ,
то есть
![]() .
Отсюда следует, что всякий элемент
множества
.
Отсюда следует, что всякий элемент
множества![]() является также элементом множества
является также элементом множества![]() ,
то есть
,
то есть![]() .
.
Значит,
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
A(BC) = (AB)(AC);
1. Доказательство с помощью диаграммы:

2. Доказательство с помощью определения равенства множеств.
Пусть хА(ВС). Тогда хА и хВС. Если хВ, то хАВ, что не противоречит сказанному, а значит, х(АВ)(АС). Если же хС, то хАС. Следовательно, х(AB)(AC). Итак, доказано, что A(BC) (AB)(AC.
Пусть теперь х (AB)(AC). Если хАВ, то хА и хВ. Отсюда следует, что хА и хВС, то есть хА(ВС). Если же хАС, то хА и хС. Отсюда вытекает, что хА и хВС, то есть хА(ВС). Таким образом, (AB)(AC) A(BC). Следовательно, A(BC) = (AB)(AC). Что и требовалось доказать.
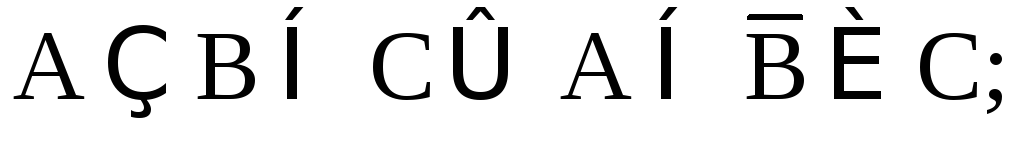 Пересечение
множеств А и В есть подмножеством
множества С тогда и только тогда, когда
множество А является подмножеством
объединения множеств не-В и С.
Пересечение
множеств А и В есть подмножеством
множества С тогда и только тогда, когда
множество А является подмножеством
объединения множеств не-В и С.

При
доказательстве достаточности мы
получили, что АВ=.
Очевидно, что С,
поэтому соотношение доказано. При
доказательстве был рассмотрен самый
общий случай. Однако здесь возможны ещё
некоторые варианты при построении
диаграмм. Например, случай равенства
АВ=С
либо
![]() ,
случай пустых множества и так далее.
Очевидно, что все возможные варианты
учесть бывает затруднительно. Поэтому
считается, что доказательство соотношений
с помощью диаграмм не всегда является
корректным.
,
случай пустых множества и так далее.
Очевидно, что все возможные варианты
учесть бывает затруднительно. Поэтому
считается, что доказательство соотношений
с помощью диаграмм не всегда является
корректным.
2. Доказательство с помощью определения равенства множеств.
Необходимость.
Пусть АВС
и элемент хА.
Покажем, что в этом случае элемент
множества А будет являться также и
элементом множества
![]() .
.
Рассмотрим
два случая: хВ
или
![]() .
.
Если
хВ,
то хАВС,
то есть хС,
и, как следствие этого,
![]() .
.
Если
же
![]() ,
то и
,
то и![]() .
Необходимость доказана.
.
Необходимость доказана.
Пусть
теперь
![]() ихАВ.
Покажем, что элемент х
также будет
элементом множества С.
ихАВ.
Покажем, что элемент х
также будет
элементом множества С.
Если
хАВ,
тогда хА
и хВ.
Поскольку
![]() ,
значитхС.
Достаточность доказана.
,
значитхС.
Достаточность доказана.
 Если
множество А является подмножеством
множества В, то тогда множество
Если
множество А является подмножеством
множества В, то тогда множество
 будет
подмножеством множества Ā.
будет
подмножеством множества Ā.
1. Доказательство с помощью диаграммы:
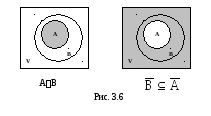
2. Доказательство с помощью определения равенства множеств.
Пусть
АВ.
Рассмотрим элемент хВ
(или
![]() ).
Аналогично:хА
(или хĀ).
То есть всякий элемент множества
).
Аналогично:хА
(или хĀ).
То есть всякий элемент множества
![]() есть также элементом множества Ā. А это
может быть в случае, если
есть также элементом множества Ā. А это
может быть в случае, если![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Задача 3.4. Выразить символически указанные области и упростить полученные выражения.

Решение.
Искомая область состоит из двух изолированных частей. Условно назовём их верхней и нижней. Множество, которое они изображают, можно описать так:
М = {xxA и хВ и хС или хС и хА и хВ}.
Из определения операций над множествами получим:
М = ((АВ)\С)(С\А\В).
Запишем это выражение с помощью основных операций – дополнения, объединения и пересечения:
![]() .
.
Упростить это выражения нельзя, поскольку имеем по одному вхождению каждого символа. Это и есть простейший вид данной формулы.
Данную область можно рассматривать как объединение множеств А\В\С и АВС. По определению M = {x xA и xВ и хС или хА и хВ и хС}. Упростим:
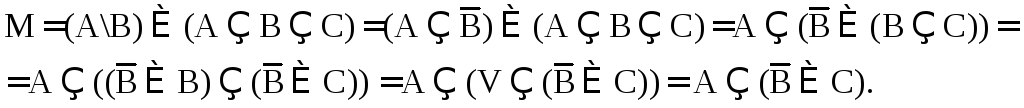
Задачи для самостоятельного решения.
1. Упростить:
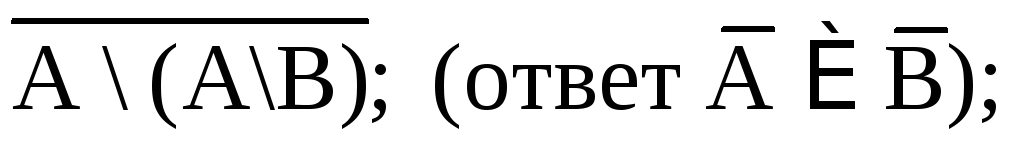
(АВ)(АВ); (ответ АВ);
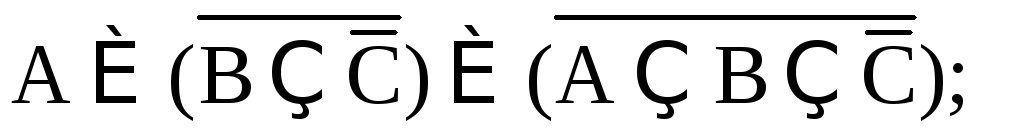 (ответ
V).
(ответ
V).
2. Доказать с помощью диаграмм, законов алгебры множеств и определения равенства множеств:
(АВ)\В = А\В;
А(ВС) = А\(А\В)(А\С);
АВ = АВ А=В;
А\В = АВ = А.
3. Выяснить, существует ли множество Х, удовлетворяющее при любом А равенству:
АХ = А; (ответ );
АХ = А; (ответ U).