22
(а) (б)
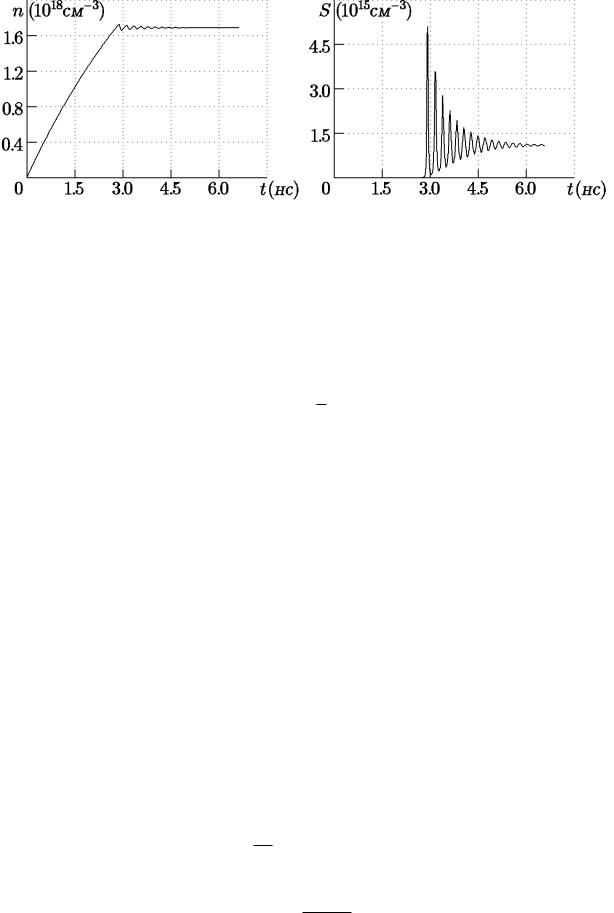
Рис. 1.9. Временные зависимости плотности носителей заряда (а) и фотонов (б) при подаче прямоугольной ступеньки тока накачки: κn = 50 см−1,
v = 9.4 × 109 см/с, τ = 5.2 нс, n0 = 1.46 × 1018см−3, g = 2.2 × 10−16 см2, |
||
β = 0.001, j = 2.5 кА/см2, j = 1.04 кА/см2. |
|
|
th |
|
|
быть приближенно представлена в виде |
|
|
n |
|
|
R = τ |
, |
(1.32) |
где τ – время жизни неравновесных носителей заряда. С учетом, что часть β от спонтанной рекомбинации вносит вклад в лазерную моду, окончательная система скоростных уравнений может быть записана следующим образом:
dn |
= |
j |
− |
n |
−vg(n −n0)S, |
(1.33) |
||||
|
dt |
ed |
τ |
|||||||
dS |
|
|
|
|
|
n |
|
|||
|
= v (g(n −n0) −κn) S + β |
|
. |
(1.34) |
||||||
dt |
τ |
|||||||||
1.2.4.Анализ переходных процессов
Результаты численного интегрирования системы уравнений (1.33) и (1.34) методом Шихмана (прил.A.1.) при ступенчатом включении тока накачки представлены на рис.1.9. Как видно, установление режима стационарной генерации сопровождается переходным процессом.
Дальнейший анализ удобно проводить в пренебрежении вкладом спонтанной рекомбинации в лазерную моду. В условиях стационарной генерации коэффициент усиления равен коэффициенту потерь. Тогда, вводя плотность порогового тока jth = edτ n0 + κgn , для стационарной плотности генерируемых фотонов Sst получаем
Sst = |
j − jth |
. |
(1.35) |
|
edvκn |
|
|
23
(а) |
(б) |
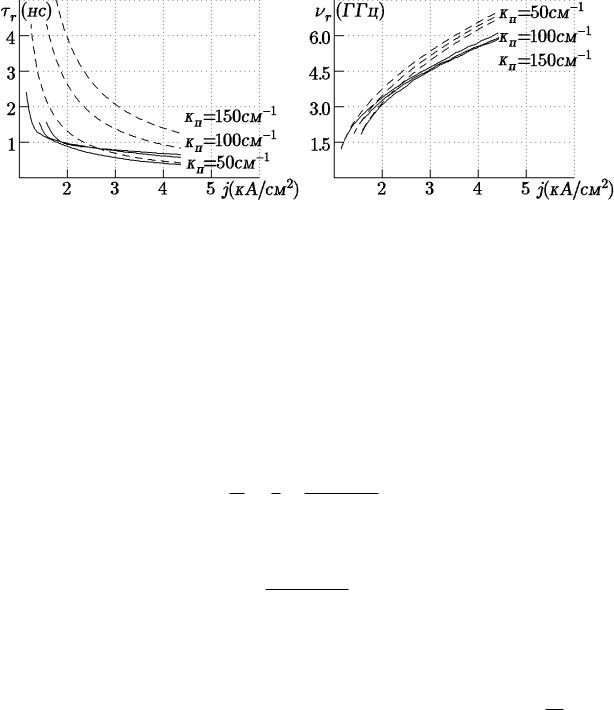
Рис. 1.10. Зависимость постоянной времени затухания начальных пичков τr (а) и частоты релаксационных пульсаций νr = wr/2π (б) от плотности тока накачки j при различных коэффициентах потерь κn. Сплошной линией даны величины, получающиеся при численном интегрировании скоростных уравнений, пунктирной - по приближенным формулам.
Рассматривая поведение решения системы (1.33), (1.34) при малых отклонениях от положения равновесия, находим выражение для постоянной времени затухания релаксационных пульсаций τr (рис.1.10а):
2 = 1 + g( j − jth),
τr τ edκn
и частоты релаксационных пульсаций wr (рис.1.10б):
w2 |
= |
vg( j − jth) |
|
− |
1 |
. |
|
|
|||||
r |
|
ed |
τr2 |
|||
(1.36)
(1.37)
При подаче прямоугольной ступеньки тока в переходном процессе формирования оптического импульса можно выделить следующие этапы:
1) Этап выполнения пороговых условий, заканчивающийся при достижении концентрацией носителей порогового значения nth = n0 + κgn . Длительность этого этапа td находится из кинетического уравнения для неравновесных носителей в предположении, что плотность фотонов до начала генерации пренебрежимо мала:
td = τ ln |
j |
(1.38) |
|
|
. |
||
|
|||
|
j − jth |
|
|
Рассчитаем плотность фотонов к концу первого этапа. Заметим, что концентрация фотонов существенно возрастает только тогда, когда концен-
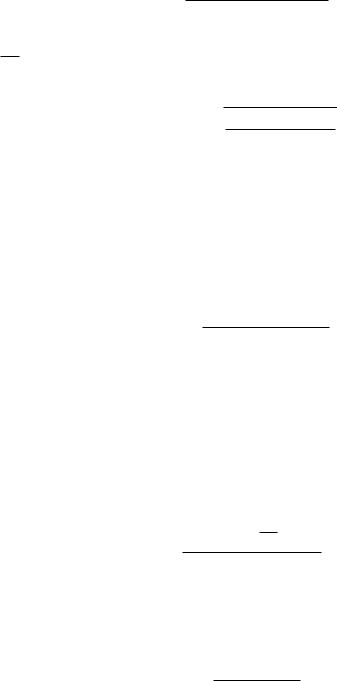
24
трация носителей приближается к пороговой. Поэтому, разделив выражение (1.34) на (1.33) и заменив в знаменателе n на nth, получим
|
dS |
= |
vgτ(n −nth)S + βn |
, |
(1.39) |
dn |
|
||||
|
|
n1 −nth |
|
||
где n1 = edjτ . После интегрирования и пренебрежения малыми слагаемыми для предпороговой плотности фотонов S0 имеем:
π |
|
S0 ≈ βnthr2vgτ(n1 −nth). |
(1.40) |
2) Этап "медленного"развития генерации. В этом случае вклад вынужденной рекомбинации в (1.33) мал. По окончании второго этапа можно считать S ≈ Sst . Плотность носителей на этом этапе достигает своего максимального значения, которое превышает пороговое на величину nmax. Интегрируя уравнение (1.33), получаем выражение для длительности второго
этапа t2 : |
= τ ln |
|
n1 −nth |
|
|
t2 |
|
. |
(1.41) |
||
|
n1 |
−nth − nmax |
|
||
Это же время t2 можно получить, интегрируя уравнение (1.34), предварительно для упрощения расчетов выразив величину n из уравнения (1.33):
S |
= v |
g τ |
ed |
− dt |
−n0 |
||
dS |
|
|
|
j |
|
dn |
|
После интегрирования получаем
τΔnmax + 1 ln Sst t2 = vg S0
n1 −nth
−κn dt. (1.42)
. (1.43)
Приравнивая (1.41) и (1.43), раскладывая выражение под логарифмом в ряд и ограничиваясь двумя первыми членами, находим
|
max ≈ s |
vgτ |
|
S0 |
|
|
|
n |
|
2 (n1 −nth) |
ln |
Sst |
. |
(1.44) |
|
|
|
|
|||||
3) Этап "быстрого"развития генерации. В уравнении для электронов (1.33) пренебрегаем спонтанной рекомбинацией и накачкой. Разделив выражение (1.34) на (1.33), получаем
dS |
≈ −1 + |
κn |
(1.45) |
|
|
|
. |
||
dn |
g(n −n0) |
|||
25
(а) |
(б) |
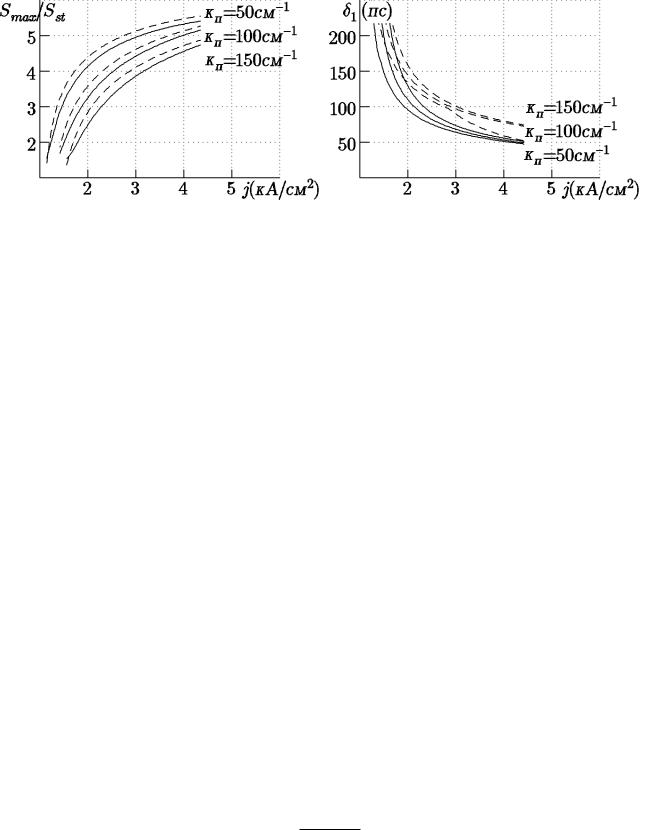
Рис. 1.11. Зависимость отношения амплитуды первого релаксационного пичка излучения Smax к стационарному значению Sst (а) и длительность первого пичка δ1 (б) от плотности тока накачки j при различных коэффициентах потерь κn. Сплошной линией даны величины, получающиеся при численном интегрировании скоростных уравнений, пунктирной - по приближенным формулам.
После интегрирования, учитывая, что n падает от nth + nmax до nth, а S растет от Sst до максимального значения Smax, находим
|
|
κ |
1 |
|
g |
nmax . |
|
|
Smax ≈ Sst + |
nmax − |
n |
ln |
+ |
|
(1.46) |
||
g |
κn |
|||||||
Оценим длительность первого пичка излучения. Складывая уравнения (1.33) и (1.34), пренебрегая накачкой и спонтанной рекомбинацией, полу-
чаем: |
dS |
|
|
|||
|
dn |
≈ −vκnS. |
|
|||
|
|
|
+ |
|
(1.47) |
|
|
dt |
dt |
||||
Считаем, что изменение концентрации за время существования импульса близко к (nmax − nth). При интегрировании по времени от момента, когда плотность фотонов равна половине максимального значения на фронте импульса, до такого же значения плотности фотонов на спаде импульса вклад от второго дифференциала S равен нулю ввиду одинаковости пределов. Значение S в правой части равенства заменяем на Smax/2. Тогда длительность первого пичка, оцененная на уровне половинной амплитуды, равна
2 nmax |
|
δ1 ≈ vκnSmax . |
(1.48) |
Точность выражений (1.46) и (1.48) иллюстрируется рис.1.11, где показаны расчетные и приближенные зависимости Smax/Sst и δ1 от плотности тока накачки.