
- •17. Біномінальний закон розподілу ймовірностей дискретної випадкової величини.
- •18. Розподіл Пуассона ймовірностей дискретної випадкової величини.
- •19. Математичне сподівання дискретної випадкової величини , його ймовірнісний зміст та властивості.
- •20. Дисперсія і середнє квадратичне відхилення дискретної випадкової величини та їх ймовірнісний зміст. Основні властивості дисперсії.
- •21.Числові характеристики середнього арифметичного однаково розподілених взаємно незалежних дискретних випадкових величин та їх практичне значення.
- •28. Дисперсія і середнє квадратичне відхилення неперервної випадкової величини.
- •33. Показниковий розподіл імовірностей неперервної випадкової величини.Графік густини й функції розподілу.
- •41. Умовні закони розподілу системи двох дискретних випадкових величин та їх числові характеристики.
- •42. Статистичний розподіл вибірки та його числові характеристики.
- •43. Емпірична функція розподілу.
- •45. Точкова оцінка математичного сподівання нормально розподіленої випадкової величини.
- •47. Інтервальні оцінки математичного сподівання нормально розподіленої випадкової величини у випадках, коли середньоквадратичне відхилення σ відоме і не відоме.
- •Інтервальна оцінка середнього квадратичного відхилення нормально розподіленої випадкової величини.
- •Задача про статистичну перевірку гіпотези і критерій узгодження.
- •53.Перевірка гіпотез про вигляд математичного сподівання нормально розподіленої випадкової величини у випадку коли дисперсія невідома.
- •Перевірка гіпотез про рівність математичних сподівань двох незалежних нормально розподілених випадкових величин
- •Перевірка гіпотез про рівність дисперсій двох незалежних нормально розподілених випадкових величин.
- •Відмінність між функціональною, статистичною та кореляційною залежностями.
- •Вибірковий коефіцієнт кореляції двовимірної випадкової величини (X, y) і визначення за його допомогою лінійного зв'язку між складовими X і y.
- •Рівняння лінійної регресії та його знаходження методом найменших квадратів.
- •Вираження рівняння лінійної регресії через коефіцієнт кореляції.
- •Статистичний розподіл вибірки двомірної випадкової величини та числові характеристики її складових.
- •Перевірка гіпотез про вигляд математичного сподівання нормально розподіленої випадкової величини у випадку коли дисперсія відома.
- •Критерій узгодження Пірсона ( критерій )для перевірки гіпотези про закон розподілу генеральної сукупності.
Класичне визначення ймовірності.
Імовірнвсть події А називається відношення числа елементарних подій, які сприяють появі події А, до числа всіх рівно можливих і попарно несумісних наслідків експерименту.Імовірність п.А = Р(А)
Р(А)=м/и.Класичне означення використовується тоді,коли м та и – скінченні й усі усі елементарні наслідки – рівно можливі.
Визначення відносної частоти події і статистичної ймовірності. Спільність і різниця між класичною ймовірністю і відносною частотою події.
Відносна
частота події А
називається числа експериментів, у яких
подія А відбулась, до числа усіх
експериментів :
 Статистичною
ймовірністю події
А називається число Р(Ф) , навколо якого
коливається відносна частота появи
цієї події в довгих серіях експериментів.
Статистичною
ймовірністю події
А називається число Р(Ф) , навколо якого
коливається відносна частота появи
цієї події в довгих серіях експериментів.
3. Геометричне визначення ймовірності та її обчислення.
Геометричним означенням користуються коли число наслідків нескінченне, але наслідки рівно можливі.Наприклад, точку, кидаємо в область G і треба оцінити можливість попасти в область g.Отже, імовірність події А називається відношення міри g до G , тобтоP (A)= mes g/mes GMes – міра область(довжина,площа_g – частина області G
4. .Поняття сумісних і несумісних подій. Як обчислити ймовірність суми несумісних подій.
Дві події А і В називають несумісними коли їх добуток є неможлива подія. Несумісність подій А і означає, що поява події А виключає можливість появи події В і навпаки.Сумісними подіями називають такі події, що поява однієї не виключає можливості появи іншої. Ймовірність суми несумісних подій: р ( А+В)=Р(А)+Р(В)
5. Повна група подій . Ймовірність протилежної події.
Події А1, А2,……..Аи утворюють повну групу, якщо в результаті виконання експкрименту принаймні одна з цих подій обов’язково відбудеться.Протилежною подією до події а називається подія, що складається з усіх елементів які не входять до події А.Отже,подія протилежна відбудеться тоді і тільки тоді, коли не відбудеться п.А.
6. Умовна ймовірність події. Імовірність добутку залежних і незалежних подій.
Умовною ймовірністю події А за умови що подія В відбудеться називають відношення : Р(А/В)=Р(АΩВ)/Р(В). Імовірність добутку залежних і незалежних подій. Для залежних: імовірність появи двох випадкових подій довірнює добутку ймовірності однієї з них та умовної ймовірності другої за умови,що відбулась перша.Для незалежних : імовірність появи двох незалежних подій дорівнює добутку їх ймовірностей.
7. Імовірність суми сумісних подій . Імовірність появи хоча б однієї з декількох подій.
Сумою 2-х сумісних подій називають подію, що складається з появи або події A, або події B, або обох їх одразу (одночасно).
Імовірність
появи хоча б однієї з двох сумісних
подій дорівнює сумі імовірностей цих
подій без імовірності їх спільної
появи:![]()
8. . Формула повної ймовірності.
Якщо Н1, Н2, ……,Ни – повна група попарно несумісних подій і Р(Ні) >0, і=1,2….и, то для будь якої п.А справедлива рівність :
Р(А)
= Формула
виражає ймовірність п.А за умови, що
відбулась одна і тільки одна з попарно
несумісних подій Н1, Н2, ……,Ни.
Формула
виражає ймовірність п.А за умови, що
відбулась одна і тільки одна з попарно
несумісних подій Н1, Н2, ……,Ни.
9. Імовірність гіпотез і формули Байєса.
Нехай набір подій Н1, Н2, ……,Ни утворює повну групу попарно несумісних подій. Тоді для будь якої випадкової події А виконується рівності Р(Ні/А)=Р(Ні)Р(А/Ні): Імовірність гіпотез Ні( І= 1,2…и) вказується якою саме умовою відбудеться п. А Щоб визначити ймовірність того, що подія А відбулась і наскільки їй при цьому сприяла гіпотеза Ні, тобто визначити Р(Ні), користуються ф-лою Баєса.
10. Послідовність незалежних випробувань за схемою Бернуллі та умови застосування.
Випробування
називаються незалежними стосовно деякої
події А, якщо ймовірність цієї події в
кожному випробуванні не залежить від
результатів інших випробувань. Серія
повторних незалежних випробуванньз
одним із можливих результатів а і неА
у кодному з яких подя а має одну і ту ж
імовірність появи Р (А)=р, називається
схемою Бернуллі.
Імовірність
Ри(М) тго, що в результаті и незалежних
випробуваннь подія А зявиться рівно м
разів ( М=0,1,2,…и), обчислюється за формулою

11. Локальна теорема Лапласа та умови застосування.
Якщо
у схемі Бернуллі кількість незалежних
випробувань є велика,то ймовірність
появи події А м разів наближено знаходимо
за формулою :![]()
12. Інтегральна теорема Лапласа.
Якщо у схемі Бернуллі и є досить великим, то ймовірність появи події А не менша ніж м1 і не більша ніж м2 разів наближено може бути знайдена за формулою :
![]() ,
де
,
де
![]() ,
,
![]() ,
а
,
а
![]() .
.
13.
Формула
Пуассона для обчислення ймовірностей
в схемі незалежних випробувань Бернуллі
та умови застосування.Формула
Пуаcсона.
Якщо в кожному з n незалежних повторних
випробувань , а n велике, то
![]()
14. Найімовірніше число появи події у послідовності випробувань за схемою Бернуллі та метод його обчислення.
Найімовірнішим
числом m0 появи події А в n незалежних
випробовуваннях називається число, для
якого ймовірність не менша ймовірності
кожного з решти можливих варіантів,
тобто
![]() ..Якщо
найімовірніше число , то повинні
виконуватись такі умови:
..Якщо
найімовірніше число , то повинні
виконуватись такі умови:
![]() (1),
(1),![]() (2)
(2)
З нерівності (1) отримується:
![]() звідки
(після скорочень) :
звідки
(після скорочень) :
![]() .
.
15. Імовірність відхилення відносної частоти події від її ймовірності.
Відхилення відносної частоти від імовірності. Імовірність того, що при проведенні n незалежних випробувань відхилення відносної частоти події А від її ймовірності за модулем не перевищить e, визначається за формулою:
![]()
16. Дискретна випадкова величина та закон розподілу її ймовірностей.
Дискретною випадковою величиною називають таку випадкову величину, яка може приймати відокремлені ізольовані одне від одного числові значення.
Дискретні випадкові величини використовуються для опису та аналізу випадкових явищ і процесів у природознавстві , економіці і т.д.
Нехай дискретна випадкова величина Х набуває значень х1, х2,….,хn з відповідними ймовірностями р1, р2,…, рn.
Законом розподілу дискретної випадкової величини називається вказана відповідність між усіма її можливими значеннями та їх імовірностями.
Оскільки в одному випробуванні події Х=х1, Х=х2, …. Х=хn утворюють повну групу, то
р1 + р2 +…..+ рn = 1
Законом розподілу дискретної випадкової величини записують таблично, графічно чи аналітично.
17. Біномінальний закон розподілу ймовірностей дискретної випадкової величини.
Якщо умови відповідають схемі Бернуллі і розподіл імовірностей визначається за формулою Бернуллі, то такий розподіл називається біномним.
Аналітичний запис закону має вигляд
P(X
= m ) =
 ( m = 0,1,2,…,n).
( m = 0,1,2,…,n).

18. Розподіл Пуассона ймовірностей дискретної випадкової величини.
Якщо у схемі Бернуллі досить великими є n a p чи q близькі до нуля і розподіл імовірностей визначається формулою Пуассона , то такий розподіл називається розподілом Пуассона.
Аналітичний
запис закону має вигляд
P
(X
= m
) =

 ,
де λ = np
/Цей
закон можна записати у формі таблиці:
,
де λ = np
/Цей
закон можна записати у формі таблиці:
 +
+



 +
+…) =
+
+…) =
 =1
=1
19. Математичне сподівання дискретної випадкової величини , його ймовірнісний зміст та властивості.
Математичне сподівання M(X) дискретної випадкової величини X називається сума добутків усіх можливих її значень на їх імовірності , тобто
M(X)
=

Якщо множина значень дискретної випадкової величини Х є нескінченна і зліченна , то
M(X)
=
причому математичне сподівання існує, якщо ряд справа у останній рівності збіжний абсолютно.
Математичне сподівання має такі основні властивості:
M(С) = С ( С – стала величина )
M(СХ) = С × M(X)
М (
 ±
±
 ± … ±
± … ±
 ) = М
(
)
±
) = М
(
)
± )
±
… ±
)
)
±
… ±
)М ( × × … × ) = М ( ) × ) ×… × ) якщо , , … , - взаємно незалежні.
M(X - M(X)) = 0
Імовірнісний зміст математичного сподівання : математичне сподівання випадкової величини X наближено дорівнює середньому арифметичному зваженому її спостережуваних значень.
20. Дисперсія і середнє квадратичне відхилення дискретної випадкової величини та їх ймовірнісний зміст. Основні властивості дисперсії.
Дисперсією D(X) , дискретної випадкової величини Х називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання, тобто
D(X)
=
 =
=
 M(X)
M(X)

Використавши властивості математичного сподівання , формулу можна звести до вигляду :
D(X)
= М ( ) – [M
(X)
=
) – [M
(X)
=
 –
[M
(X)
–
[M
(X)
У випадку , коли множина різних значень дискретної випадкової величини Х є нескінченна і зліченна , то
D(X)
=
 - M
(X)
- M
(X)
 або
або
D(X)
=
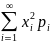 –
[M
(X)
,
–
[M
(X)
,
за умови , що числові ряди в правих частинах цих формул є збіжні.
Дисперсія має такі основні властивості:
D(X)≥0
D(С) = 0
D(СX) =
 × D(X)
× D(X)
D ( ± ) = D ( ) ±
 )
(для
незалежних
,
)
)
(для
незалежних
,
)D ( × ) = D ( ) × ) + (М ( )
 + (М
(
)
+ (М
(
)
Cереднім квадратичним відхиленням ДВВ Х називають корінь квадратний з дисперсії D(X) і позначають σ(Х) , тобто
σ(Х)
=

21.Числові характеристики середнього арифметичного однаково розподілених взаємно незалежних дискретних випадкових величин та їх практичне значення.
Чисельні
характеристики ( математичне сподівання
, дисперсія , середнє квадратичне
відхилення ) середнього арифметичного
 n
взаємно незалежних і однаково розподілених
дискретних випадкових величин
,
, … ,
виражаються такими рівняннями :
n
взаємно незалежних і однаково розподілених
дискретних випадкових величин
,
, … ,
виражаються такими рівняннями :
M
(
)= M,
D
(
)=
 , σ
=
, σ
=

Значення середнього арифметичного результатів вимірювань ознаки випадкової величини є надійнішим і ближчим до істинної характеристики цієї ознаки , ніж окремий результат.
23.Функція розподілу випадкової величини та її графік.
Функцією розподілу ( інтегральною функцією розподілу , інтегральним законом розподілу ) випадкової величини Х називається ймовірність того, що в результаті випробування вона набуде значення , меншого за х , тобто
F (X) = P (X < x)

![]()
24.Формула для обчислення ймовірності попадання значень випадкової величини Х в заданий інтервал , яка виражається через функцію розподілу.
Ймовірність того , що випадкова величина Х набуде значення з проміжку [a ; b), дорівнює приросту функції розподілу на цьому проміжку , тобто Р (а ≤ Х < b) = F (b) – F (a)
25.Густина розподілу неперервної випадкової величини та її графік.
Густиною розподілу неперервної випадкової величини Х називається функція f(x) , яка дорівнює першій похідній від функції розподілу F (x) , тобто
f(x)
=
 (x)
(x)

26.Формула для обчислення ймовірності попадання значень випадкової величини в заданий інтервал , яка виражається через густину розподілу.
Ймовірність
того, що неперервна випадкова величина
Х набуде значення з інтервалу ( а; b),
дорівнює невизначеному інтегралу від
густини її розподілу в межах від а до
b,
тобто :Р
(а < Х <
b)
=
27. Математичне сподівання неперервної випадкової величини.
Математичне сподівання неперервної випадкової величини Х називають число М(Х), яке визначається рівністю:M(X) =
якщо
можливі значення НВВ Х належать інтервалу
( а; b)
, абоM(X)
= ,
якщо можливі значення НВВ Х належать
усій осі Ox
.У другому випадку припускається , що
останній інтеграл збігається абсолютно
, тобто існує
,
якщо можливі значення НВВ Х належать
усій осі Ox
.У другому випадку припускається , що
останній інтеграл збігається абсолютно
, тобто існує
 Математичне
сподівання неперервної випадкової
величини є точки числової осі , яка
характеризує її «середнє» значення або
центр розподілу її значень.
Математичне
сподівання неперервної випадкової
величини є точки числової осі , яка
характеризує її «середнє» значення або
центр розподілу її значень.
