2.2 Рекомендації щодо відбору факторів

При виборі факторів, котрі включаються в регресійну модель для аналізу системи, слід виходити із наступних основних принципів.

1. Із апріорно вибраної для аналізу множини факторів необхідно використовувати мінімальну кількість факторів, котрі в основному визначають середнє значення результативної ознаки (принцип простоти). Зайве розширення моделі приводить до труднощів економічної інтерпретації одержаних параметрів і до того, що рівняння буде відображати не тільки тенденції в розвитку економічного показника на фоні випадкових коливань, але і самі випадкові коливання.

2. кожна причина в рівнянні повинна бути представлена однією ознакою; неприпустимим є водночас використовувати синтетичні показники і їх складові частини (принцип неповторення).

3. В багатофакторну модель слід включати лише такі фактори, котрі в ланцюзі “причини – слідства” займають один і той же рівень (принцип рівноправності або непідпорядкованості факторів). Як правило, рекомендується використання факторів нижчого рівня.

4. В модель слід включати тільки фактори, які визнають суттєвими для якісної оцінки даної проблеми або галузі науки, до якої відноситься об’єкт дослідження (принцип відповідності кількісного і якісного аналізу). Ця вимога пов’язана з тим, що всі причини, за якими формується досліджувана ознака, можна розділити на головні і другорядні, пов’язані з індивідуальними відхиленнями.

5. фактор повинен мати кількісний вираз (принцип визначеності). Показник має кількісний вираз, якщо його можна виміряти, тобто однозначно виразити за допомогою числа. Якщо який–небудь показник неможливо виразити у вигляді кількості або хоча б величини, такий фактор не можна включати в математичну модель. Показник має характер величини, якщо його вимірити не можна, але можна оцінити і однозначно розставити по порядку, по ступені впливу, порівняно з іншими аналогічними показниками.

6. В моделі можна використовувати лише фактори, які мають з результативною оцінкою щільніший зв’язок, ніж між собою (принцип припустимої мультиколінеарності). Мультиколінеарність має місце у випадках, коли залежні змінні сильно корелюють між собою і одна з них може бути подана як лінійна функція інших. Наявність в моделі лінійно залежних факторів свідчить про те, що вони характеризують одну і ту ж сторону явища, тобто дублюють один одного. Одержані при цьому параметри моделі будуть не стійкими (мають значну середньоквадратичну помилку), тому їх економічна інтерпретація іноді неможлива. Крім того, наявність мультиколінеарності між факторами, які входять в математичну модель, приводить до того, що матриця системи нормальних рівнянь буде погано обумовленою або не має розв’язку. Це збільшує труднощі розрахунків і викликає ненадійність результатів рішення.

Відбір факторів необхідно виконувати на основі існуючої статистичної звітності.

2.3 Методика комплексної систематизації статистичної інформації

Апріорно відібраний статистичний матеріал спочатку систематизується за однією якісною ознакою. Систематизація полягає у побудові ряду розподілу досліджуваної ознаки і її повного статистичного аналізу.

Далі проводиться систематизація за двома або більшим числом ознак. Для цього використовуються методи кореляційного аналізу, котрі дозволяють відібрати найбільш суттєві фактори і встановити наявність кореляційного зв’язку між досліджуваними залежними і незалежними ознаками.

Надійність результатів аналізу тим вища, чим більший об’єм вибірки, за якою вони розраховуються. Мінімальне число спостережень (об’єм вибірки) визначається на основі співвідношення

, (2.2)

де N — кількість спостережень;

m — число досліджуваних факторів - аргументів.

Систематизація виконується в такій послідовності.

1. статистичні дані спостережень групуються з урахуванням специфіки роботи системи і її окремих елементів.

2. По кожному показнику майбутньої моделі розраховують основні статистичні характеристики: середнє вибіркове, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації.

3. У випадку, коли вихідні дані зібрані на декількох об’єктах або в різні періоди часу, тобто представлені окремими незалежними вибірками, їх необхідно перевірити на статистичну однорідність сукупності. Перевірка виконується за результативним показником і полягає в наступному.

Нехай для k часткових вибірок маємо об’єми вибірок:

,

відповідно вибіркові середні:

,

дисперсії:

.

Із даної величини вибираємо дві часткові вибірки відповідно з максимальним і мінімальним значеннями і для них розраховуємо критерійt_ij за формулами (1.7), (1.8). Обчислене значення t_ij порівнюється з табличним t_α, визначеним за таблицею функції Φ(t) Лапласа (для великих вибірок) або за таблицею t–розподілу Стьюдента (для малих вибірок). Якщо t_ij  t_α , то сукупність буде однорідною.

4. Виключення із статистичних даних грубих аномальних значень досліджуваних параметрів згідно з формулами (1.5) або (1.6).

5. Після упорядкування статистичної інформації виконується перевірка нормальності розподілу результативної ознаки Y.

6. Перевірка достатності спостережень. Перевірка виконується за формулою (1.13) або (1.14).

7. Складання і аналіз кореляційної матриці r_ij між факторами x₁, x₂, …, x_m:

. (2.3)

Коефіцієнти r_ij характеризуються такими співвідношеннями:

.

Значення r_ij , що близькі до нуля, свідчать про відсутність взаємозв’язку між факторами, а наближення їх до одиниці – на наявність функціонального зв’язку.

8. Виявлення наявності мультиколінеарності. Наявність мультиколінеарності можна визначити двома методами.

метод порівняння абсолютних значень |r_ij| коефіцієнтів кореляції.. Із множини факторів x₁, x₂, …, x_n виділяють такі фактори, у яких значення коефіцієнта |r_ij| перевищує 0.8. такі фактори вважають колінеарними.

Якщо жодний з елементів матриці |r_ij| не перевищує 0.8, доцільно наявність мультіколінеарності визначити за допомогою кореляційних відношень |_ij|.

Внаслідок симетричності матриці коефіцієнтів r_ij для аналізу використовується тільки одна половина матриці. При наявності пари колінеарних факторів в модель як незалежний доцільно включити фактор, який має меншу дисперсію.

Як приклад розглянемо матрицю коефіцієнтів кореляції (таблиця 2.1) між шістьма (x₁, x₂, x₃, x₄, x₅, x₆) факторами, взаємопов’язаними з результативною ознакою виробничого процесу y=f(x₁, x₂, x₃, x₄, x₅, x₆).

Таблиця 2.1 – Матриця коефіцієнтів кореляції

	х1	х2	х3	х4	х5	х6
x1	1.0000	0.8816	0.6313	0.3507	0.3110	0.5301
х2		1.0000	– 0.6447	– 0.5047	– 0.3922	– 0.5603
х3			1.0000	0.6244	0.4880	0.6426
х4				1.0000	0.4810	0.8812
х5					1.0000	0.1906
х6						1.0000

Із матриці виходить, що між факторами x₁ і x₂ та x₄ і x₆ існує колінеарність, так як їх коефіцієнти регресії r₁₂ = 0.8816 і r₄₆ = 0.8812 перевищують 0.8. Ці показники характеризують одну і ту ж сторону процесу. Тому один із них з подальшого аналізу слід виключити. Виключимо фактори, які мають більшу дисперсію. Порівнюючи дисперсії факторів (S²_х1 = 70, S²_х2 = 18, S²_х4 = 19, S²_х6 = 10), приходимо до висновку, що з подальшого аналізу слід виключити фактори х₁ та х₄. З урахуванням цього модель результативного показника можна представити у вигляді y = f(х₂, х₃, х₅, х₆).

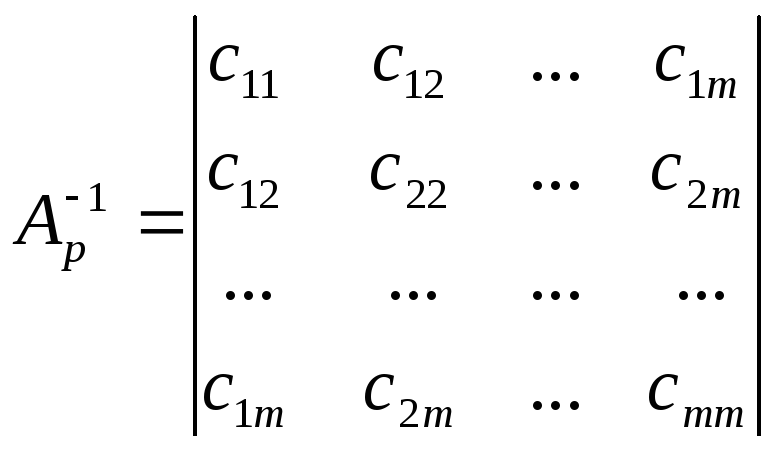
Метод порівняння на основі критерію Фішера. Розрахункове значення критерію F визначається на підставі матриці парних коефіцієнтів кореляції r_ij. Для цього матриця (2.1) перетворюється в обернену матрицю

. (2.4)

Для перевірки мультиколінеарності розраховується для кожного фактора показник F_i за формулою

, (i=1, 2, ..., m), (2.5)

де N – кількість спостережень;

C_ij — діагональний елемент оберненої матриці.

Розраховане значення F_i порівнюється з табличним значенням розподілу Фішера (додаток Д5) за числом ступенів свободи f₁=N–m і f₂=m–1: F_5% ( f₁, f₂ ) і F_1% ( f₁, f₂ ).

Якщо F_i < F_5% , то при 5%–му рівні значущості стверджуємо гіпотезу відсутності мультиколінеарності –го аргументу з іншими в генеральній сукупності. Якщо F_i > F_1% , то при 1%–му рівні значущості відхиляємо гіпотезу відсутності мультиколінеарності i–го аргументу з іншими в генеральній сукупності. У цьому випадку включення –го аргументу в загальну модель вважають неприпустимим. Висновки щодо виключення аргументу супроводжуються економічним аналізом.

Зберігши в сукупності тільки немультиколінеарні аргументи, складаємо нову кореляційну матрицю (2.3), обернену їй (2.4) і повторюємо перевірку з допомогою (2.5) до повного “очищення” від мультиколінеарності.

Порядок виявлення мультіколінеарності за даним методом розглянемо на конкретному прикладі.

Статистична вибірка нараховує N=154 спостереження. Кореляційна таблиця для чотирьох факторів (х₁, х₂, х₃, х₄), які характеризують виробничий процес, має вигляд

.

після обернення цієї матриці отримуємо

.

для перевірки мультиколінеарності складемо вирази F_i (i=1, 2, 3, 4) за формулою (2.5):

;

;

;

.

Розраховуємо число ступенів свободи

;

.

За таблицею розподілу Фішера (додаток Д5) маємо:

F _5% (150; 4 ) =8.537 i F_1%(150; 3)=26.125.

Порівнюючи F_i з табличним значенням розподілу Фішера, приходимо до висновку:

– при 5%–му рівні значущості лише для другого фактора х₂ відсутня мультиколінеарність ( F₂ < F_1% ), і його можна включити в рівняння регресії;

– при 1%–му рівні значущості всі аргументи х₁, х₂, х₃, х₄ можна включити в регресійну залежність, на підставі того, що

F_i (150; 3) < F_1%(150; 3).

9. Встановлення кореляційного зв’язку між залежними і незалежними змінними. Якщо кожному значенню аргументу (фактору) х відповідає ряд розподілу функції (результату) Y_i при зміні x ці ряди закономірно змінюють своє положення, тоді можна стверджувати, що Y знаходиться у кореляційній залежності від x.

Наявність кореляційного зв’язку між досліджуваними показниками встановлюють шляхом систематизації статистичних даних, яка може бути виконана за двома формами – графічною і табличною.

Графічною формою систематизації статистичного матеріалу за двома якісними оцінками є поле кореляції. При побудові поля кореляції по осі абсцис X відмічається значення аргументу (факторіальна оцінка), а по осі ординат Y – значення функції (результативна оцінка).

Результати кожного випробування відмічаємо точкою в системі координат (X, Y). Для нанесення точок на поле кореляції слід користуватися тільки вихідною статистичною інформацією, яка не підпадала під будь–яку попередню обробку. При побудові поля кореляції весь проміжок спостережень ознак розбивається на m інтервалів. При кількості спостережень від 30 до 100 проміжок варіацій ознак ділиться на 5–10 інтервалів. Розмір інтервалу дорівнює

, (2.6)

де a_max, a_min - відповідно максимальне і мінімальне значення оцінки.

Основні прийоми визначення кореляційного взаємозв’язку ознак розглянемо на методичному прикладі визначення взаємозалежності між величиною простоїв вагонів в транспортній системі (результативна ознака Y) і кількості завантажених вагонів (факторіальна ознака X), які надходять в систему. Статистичні дані наведені в таблиці 2.2.

Для досліджуваних ознак приймаємо число інтервалів m=10. тоді розміри інтервалів будуть дорівнювати:

• для ознаки Y

;

– для ознаки X

.

Приклад графічної форми систематизації статистичного матеріалу у вигляді поля кореляції наведений на рисунку 2.1.

рисунок 2.1 – Поле кореляції і емпірична лінія регресії.

При табличній формі систематизації складають так звану кореляційну таблицю (табл. 2.3). для цього на поле кореляції накладається координатна сітка згідно з прийнятою системою інтервального розподілу за факторіальною і результативною оцінками. Далі підраховується кількість точок (частот) в кожній клітинці координатної сітки.

Результати підрахунків, а також горизонтальні і вертикальні підсумки частот записуються в кореляційну таблицю.

Аналізуючи таблицю 2.3, можемо визначити, що її вертикальний підсумковий стовпець виражає інтервальний ряд розподілу за результативною ознакою, а горизонтальний підсумковий рядок – за функціональною ознакою. Крім того, внутрішні стовпчики або рядки також утворюють ряди розподілу для функції або аргументу Аналіз поля кореляції і кореляційної таблиці показує, що величина загального простою вагонів в системі знаходиться у кореляційній залежності від їх кількості. Про це свідчать дві обставини: 1) кожному значенню аргументу x відповідає ряд розподілу функції y; 2) при зміні x ці ряди закономірно змінюють своє положення: при збільшенні x ряди розподілу y зміщуються догори, тобто величина простою вагонів збільшується.

Таблиця 2.2 – Статистичні дані

Номер спостереження	Показники		Номер спостереження	Показники
	Y	X		Y	X
1	1120	39	31	1026	23
2	120	19	32	638	24
3	671	16	33	484	13
4	742	22	34	580	7
5	651	15	35	474	15
6	482	14	36	576	17
7	151	5	37	546	12
8	367	14	38	562	17
9	714	20	39	262	10
10	505	6	40	434	17
11	484	5	41	638	9
12	126	5	42	203	4
13	564	13	43	312	8
14	497	17	44	357	8
15	429	10	45	120	7
16	396	14	46	337	8
17	240	6	47	625	14
18	210	10	48	662	34
19	396	7	49	802	15
20	498	17	50	253	5
21	657	15	51	483	13
22	420	20	52	781	16
23	815	18	53	276	16
24	413	13	54	327	6
25	493	10	55	488	9
26	567	22	56	784	22
27	859	20	57	417	11
28	422	10	58	724	17
29	484	26	59	300	6
30	757	20	60	620	17

Таблиця 2.3 – Кореляційна таблиця залежності Y від X

Простій вагонів Y, год.	Кількість вагонів в системі X									Разом
	4–8	8–12	12–16	16–20	20–24	24–28	28–32	32–36	36–40
1020–1120									1	1
920–1020					1					1
820–920				1						1
720–820			4	2	2					8
620–720		1	4	1	1			1		8
520–620	1	1	1	3	1					7
420–520	2	4	3	3		1				13
320–420	3	2	3	1						9
220–320	2	1	1							4
120–220	6	1		1						8
Разом	44	10	16	12	5	1	–	1	1	n=60

10. Визначення форми зв’язку. Форма зв’язку визначаються шляхом побудови на графіку кореляційного поля емпіричної лінії регресії. Для цього на підставі кореляційної таблиці або безпосередньо кореляційного поля розраховують середні значення y для кожного ряду розподілу за формулою

, (2.7)

де – середнє зважене значення функції;

y – середнє інтервальне значення функції;

–абсолютні частоти y в кожному інтервалі.

Для нашого прикладу маємо:

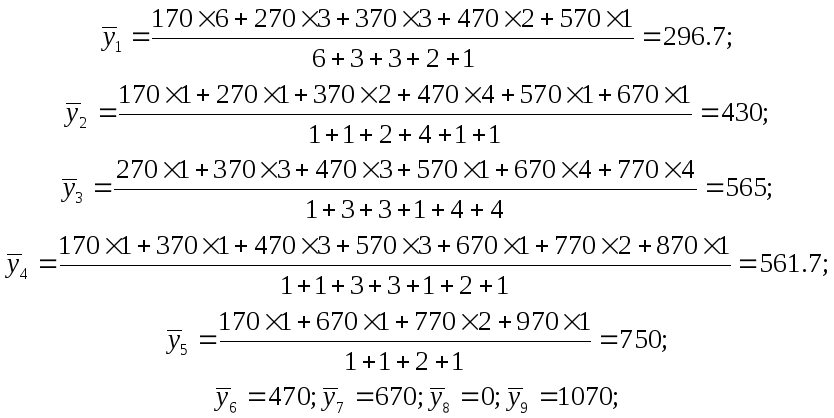
На графіку кореляційного поля (рис.2.1) відмічаємо клітинки, які відповідають обчисленим значенням . Послідовно з’єднавши позначки відрізками прямих ліній, отримаємо емпіричну лінію регресії.