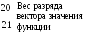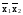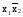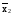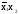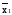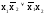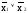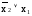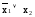21. Элементарные переключательные функции

Переключательные (логические) функции, соответствующие логическим операциям В²В, называют элементарными. Количество переключательных (логических) функций от n переменных определяется выражением 2²ⁿ, поскольку |Bⁿ|=2ⁿ, а на каждом из 2ⁿ наборов переключательная (логическая) функция может принимать одно из значений из того же множества В (табл. 23).

Таблица 23

Переключательные функции от n переменных

№	Набор	Номер логической функции
п/п	значений переменных	0	1	2	3	...	22n-1
1	00...00	0	1	0	1	...	1
2	00...01	0	0	1	1	...	1
3	00...10	0	0	0	0	...	1
4	00...11	0	0	0	0	...	1
. . .	. . .	. . .	. . .	. . .	. . .	...	. . .
22	11...11	0	0	0	0	...	1

Например, рассмотрим все переключательные (логические) функции одной переменной (табл. 24).

Таблица 24

Переключательные функции одной переменной

	Переключательная (логическая) функция
х	f0(x)	f1(x)	f2(x)	f3(x)
0	0	1	0	1
1	0	0	1	1

Поскольку 2²¹=4, то имеется четыре логических функции одной переменной, две из них – константы: f₀(x)=0, f₃(x)=1 (f₀(x) – константа нуля, f₃(x) – константа единицы). Здесь номер функции означает десятичное число, соответствующее двоичному числу, записанному в соответствующем столбце табл. 24.

Функция f₂(x)=х, т.е. совпадает со значением переменной. Эта функция называется функцией повторения. Функция 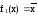нам уже известна – это инверсия.

Можно заметить, что для каждой функции одной переменной существует инверсная ей функция:

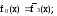
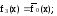
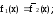
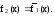
Элементарные переключательные (логические) функции двух переменных

Рассмотрим все функции двух переменных (табл. 25).

Таблица 25

Переключательные функции двух переменных

		20	21	22	23
		Набор					Название		Формула
20	х1	0	1	0	1	функции
21	х2	0	0	1	1
	f0	0	0	0	0	Константа 0		0
	f1	1	0	0	0	Функция Пирса (Вебба), «стрелка Пирса», ИЛИ-НЕ		х1х2=
	f2	0	1	0	0	Запрет х2
	f3	1	1	0	0	Отрицание х2
	f4	0	0	1	0	Запрет х1
	f5	1	0	1	0	Отрицание х1
	f6	0	1	1	0	Сложение (сумма) по mod2		х1х2=
	f7	1	1	1	0	Функция Шеффера, «штрих Шеффера», И-НЕ		х1|х2=
	f8	0	0	0	1	Конъюнкция, И		х1х2
	f9	1	0	0	1	Эквиваленция (эквивалентность)		х1х2=
	f10	0	1	0	1	Повторение х1		х1
	f11	1	1	0	1	Импликация х2 в х1		х2х1
	f12	0	0	1	1	Повторение х2		х2
	f13	1	0	1	1	Импликация х1 в х2		х1х2
	f14	0	1	1	1	Дизъюнкция, ИЛИ		х1х2
	f15	1	1	1	1	Константа 1		1

Всего таких функций имеется 2²²=2⁴=16. Есть функции, зависящие только от одной переменной. Есть функции, не зависящие от переменных, – константы 0, 1. Такие функции называют вырожденными:

f₃(x₁x₂)=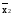;f₅(x₁x₂)=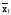;f₁₀(x₁x₂)=х₁; f₁₂(x₁x₂)=х₂;

f₀(x₁x₂)=0; f₁₅(x₁x₂)=1.

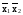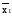Некоторые функции мы тоже уже знаем: конъюнкцию f₈(x₁x₂)=х₁х₂ (точку между х₁ и х₂ опускаем); эквиваленцию (эквивалентность) f₉(x₁x₂)=х₁х₂=х₁х₂ (здесь эквиваленция представлена в виде дизъюнкции двух конъюнкций, что можно доказать, составив таблицу истинности); импликацию f₁₁(x₁x₂)=х₂х₁=х₁, f₁₃(x₁x₂)=х₁х₂=х₂; дизъюнкцию f₁₄(x₁x₂)=х₁х₂.

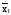
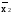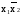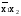Кроме этого, имеются другие функции, зависящие от двух переменных: f₁(x₁x₂)=– функция Пирса (Вебба) («стрелка Пирса»);f₂(x₁x₂)=– запрет х₂; f₄(x₁x₂)=– запрет х₁; f₆(x₁x₂)=x₁x₂ –сложение по модулю 2 (функция, инверсная эквиваленции); f₇(x₁x₂)=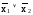– функция Шеффера («штрих Шеффера»).