
Лекции
.docЛекции.
-
Механика.
-
Кинематика и динамика вращательного движения. Момент инерции. Момент импульса. Основное уравнение динамики вращательного движения. Закон сохранения момента импульса. Кинетическая энергия вращающегося тела.
Простейшей формой движения материи является механическое движение. Оно представляет собой изменение положения тела или его отдельных частей в пространстве, т.е. относительно друг друга. Основная задача механики состоит в ответе на вопрос: где будет находиться тело в интересующий нас момент времени.
Любое движение в механике может быть представлена как комбинация двух основных видов движения: поступательного и вращательного.
Рассмотрим наиболее простой случай вращательного движения: вращение абсолютно твердого тела вокруг неподвижной оси.
Тело называется абсолютно твердым, если расстояние между его любыми двумя точками неизменно. Понятно, что это понятие является физической абстракцией. Реально этому условию удовлетворяют тела, деформациями которых при решении тех или иных задач можно пренебречь.
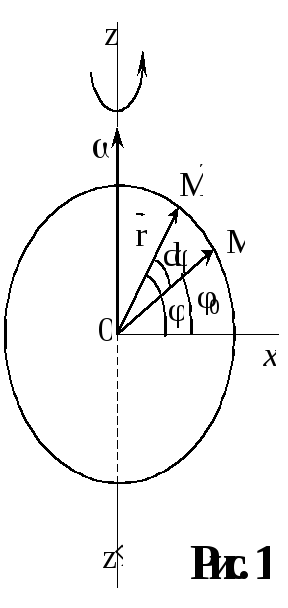
При вращении разные точки твёрдого тела движутся по окружностям, центры которых образуют прямую. Эта прямая и называется осью вращения. Легко заметить, что угловые перемещения всех точек за один и тот же промежуток времени t будут при этом одинаковыми. По этой причине положение вращающегося тела целесообразно определять углом, на который оно поворачивается относительно своего начального положения. Уравнением вращательного движения в этом случае будет функция = f(t), которая будет иметь один и тот же вид для всех точек тела. Получим выражение этой функции в общем виде. Для этого достаточно рассмотреть движение одной из точек тела вокруг оси.
 Пусть
твердое тело вращается вокруг оси
Пусть
твердое тело вращается вокруг оси
![]() .
Траектория движения точки М будет
представлять собой окружность, плоскость
которой перпендикулярна
.
Траектория движения точки М будет
представлять собой окружность, плоскость
которой перпендикулярна
![]() ,
а центр 0 лежит на этой прямой. Положение
произвольной точки М на траектории
будем определять углом ,
который образует радиус-вектор
,
а центр 0 лежит на этой прямой. Положение
произвольной точки М на траектории
будем определять углом ,
который образует радиус-вектор
![]() ,
проведенный из центра окружности к
точке М, с лучом 0х, лежащим в плоскости
траектории и выбранным за начало отсчета.
,
проведенный из центра окружности к
точке М, с лучом 0х, лежащим в плоскости
траектории и выбранным за начало отсчета.
В СИ измерение угла производится в радианах. Угол в 1 радиан – это центральный угол, который опирается на дугу длинной равной радиусу окружности r. Т.е., чтобы определить угол в радианах надо длину дуги разделить на её радиус кривизны:
![]() (1)
(1)
Рассмотрим основные кинематические
параметры вращательного движения. Пусть
за бесконечно малый промежуток времени
dt материальная точка из положения М
переместится в положение
![]() ,
пройдя путь ds. При этом
радиус-вектор
,
пройдя путь ds. При этом
радиус-вектор
![]() повернётся на бесконечно малый угол
d.
повернётся на бесконечно малый угол
d.
Угловая скорость
– это вектор численно равный углу
поворота радиус-вектора
![]() за единицу времени и направленный так,
что с его острия движение точки совершается
против часовой стрелки. Начало
за единицу времени и направленный так,
что с его острия движение точки совершается
против часовой стрелки. Начало
![]() находится в точке О.
находится в точке О.
![]() .
.
![]() .
(2)
.
(2)
Время, за которое тело совершает один полный оборот, называется периодом вращения (Т). Т.к. угол поворота, соответствующий одному полному обороту = 2 рад, то при равномерном движении
![]() . (3)
. (3)
Величину равную числу оборотов тела за единицу времени называют частотой вращения n:
![]() ;
;
![]() . (4)
. (4)
Уравнение равномерного вращательного движения (ω = const) получим, решив дифференциальное уравнение (2):
![]() .
(5)
.
(5)
При неравномерном вращении быстрота изменения угловой скорости характеризуется угловым ускорением :
![]() .
.
![]() . (6)
. (6)
![]() – это вектор, расположенный на оси
вращения и направленный, так как и
– это вектор, расположенный на оси
вращения и направленный, так как и
![]() ,
если скорость растет, и в противоположном
направлении, если скорость уменьшается.
,
если скорость растет, и в противоположном
направлении, если скорость уменьшается.
В общем случае, уравнение равноускоренно вращательного движения (β = const) можно получить, решив дифференциальное уравнение (6) относительно :
= 0 + t, (7)
![]() (8).
(8).
Для описания движения по круговой траектории можно использовать и уже знакомые нам линейные кинематические параметры. Например, скорость движения точки по траектории:

![]() .
.
![]() .
(9)
.
(9)
Эта
скорость при переходе из одной точки
траектории (М) в другую (![]() )
будет меняться в общем случае как по
величине, так и по направлению (рис.2):
)
будет меняться в общем случае как по
величине, так и по направлению (рис.2):
![]() (10)
(10)
Разложим вектор
![]() на две составляющие:
на две составляющие:![]() –
направленную вдоль
–
направленную вдоль
![]() и
и
![]() –
проведенную так, что
–
проведенную так, что
![]() .
Из чертежа видно, что dτ
–равна приращению модуля скорости
.
Из чертежа видно, что dτ
–равна приращению модуля скорости
![]() ,
а
,
а
![]() определяет изменение направления
вектора скорости
определяет изменение направления
вектора скорости
![]() при переходе точки тела из положения М
в
при переходе точки тела из положения М
в
![]() .
.
![]() (11).
(11).
Разделив (11) на dt, получим:
![]() (12)
(12)
Так как
![]() – это полное линейное ускорение
– это полное линейное ускорение
![]() ,
то (12) перепишется
,
то (12) перепишется
![]() , (13)
где
, (13)
где
![]() – тангенциальное ускорение, которое
характеризует быстроту изменения
скорости по величине (по модулю); dn/dt
= an –
нормальное ускорение, которое определяет
„быстроту” изменения направления
скорости.
– тангенциальное ускорение, которое
характеризует быстроту изменения
скорости по величине (по модулю); dn/dt
= an –
нормальное ускорение, которое определяет
„быстроту” изменения направления
скорости.
Установим взаимосвязь линейных и угловых параметров движения по окружности. Из соотношения (1)
s = r. (14)
Продифференцировав правую и левую часть по t, имеем:
![]() ,
т.е. = r
. (15)
,
т.е. = r
. (15)
Эта формула определяет взаимосвязь модуля линейной скорости и модуля угловой скорости . Дифференцируем (15) еще раз по t, получим для тангенциального ускорения:
![]() ,
а =
r. (16)
,
а =
r. (16)
Из треугольника
![]() при радианной мере малых углов:
при радианной мере малых углов:
dn
= ·sind
= ·d.
Но
![]() ,
тогда
,
тогда
![]() .
.
Дифференцируя по t правую и левую часть последнего равенства, получим:
![]() отсюда
отсюда
![]() . (17)
. (17)
Учитывая (15), из (17) получим:
an = 2r (18)
Из
АВС (dυ)2 = (dυτ)2
+ (dυn)2
или после деления на (dt)2
–
![]() .
С учетом (16) и (18)
.
С учетом (16) и (18)
![]() . (19)
. (19)
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
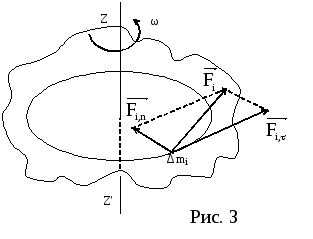 Установим взаимосвязь между кинематическими
и динамическими параметрами вращательного
движения. Пусть твердое тело вращается
вокруг неподвижной оси ZZ′.
Т.к. все точки тела движутся по окружностям,
плоскость которых перпендикулярна оси
вращения, то это означает, что
равнодействующие сил приложенных к
каждой точке лежат в плоскости траекторий.
Разложим равнодействующую сил
Установим взаимосвязь между кинематическими
и динамическими параметрами вращательного
движения. Пусть твердое тело вращается
вокруг неподвижной оси ZZ′.
Т.к. все точки тела движутся по окружностям,
плоскость которых перпендикулярна оси
вращения, то это означает, что
равнодействующие сил приложенных к
каждой точке лежат в плоскости траекторий.
Разложим равнодействующую сил
![]() ,
приложенную к элементу массы mi
на две составляющие:
,
приложенную к элементу массы mi
на две составляющие:![]() –
вдоль радиуса
–
вдоль радиуса
![]() и
и
![]() –
касательную к траектории. Нормальная
составляющая сил
–
касательную к траектории. Нормальная
составляющая сил
![]() ,
линия действия которой лежит в плоскости
траектории, проходит через ZZ′
и обеспечивает центростремительное
ускорение элемента массы mi
и не влияет на величину углового
ускорения. Составляющая
,
линия действия которой лежит в плоскости
траектории, проходит через ZZ′
и обеспечивает центростремительное
ускорение элемента массы mi
и не влияет на величину углового
ускорения. Составляющая
![]() вызывает тангенциальное ускорение
вызывает тангенциальное ускорение
![]() .
По второму закону Ньютона
.
По второму закону Ньютона
![]() . (20)
. (20)
С учетом (16)
Fi,=miri. (21)
Умножив (21) на ri, получим:
![]() , (22)
, (22)
![]() , (23)
, (23)
где
![]() – момент силы
– момент силы
![]() относительно оси ZZ′.
относительно оси ZZ′.
Моментом
силы называется вектор, модуль которого
равен произведению модуля силы на длину
плеча. Направление вектора
![]() перпендикулярно к плоскости, в которой
лежит вектор силы, и определяется по
правилу буравчика.
перпендикулярно к плоскости, в которой
лежит вектор силы, и определяется по
правилу буравчика.
Плечом силы называется кратчайшее расстояние от оси вращения до линии действия силы.
Скалярная
величина
![]() называется момент инерции материальной
точки относительно оси вращения ZZ′.
называется момент инерции материальной
точки относительно оси вращения ZZ′.
Просуммируем (23) по
всем элементам массы тела:
![]() .
Получим:
.
Получим:
![]() или в векторном виде
или в векторном виде
![]() (24)
(24)
Здесь
![]() -
результирующий момент силы, действующий
на тело;
-
результирующий момент силы, действующий
на тело;
![]() - момент инерции тела.
- момент инерции тела.
Равенство
(24) называется основным уравнением
динамики вращательного движения. Т.к.
скалярная величина J
всегда положительная, то векторные
величины
![]() и
и
![]() всегда направлены в одну сторону вдоль
оси вращения тела.
всегда направлены в одну сторону вдоль
оси вращения тела.
Основное уравнение динамики вращательного движения по форме сходно с математическим выражением второго закона Ньютона :
![]() ↔
↔
![]()
Из сопоставления вытекает, что при вращательном движении роль силы играет момент силы (вращательный момент), а инертные свойства тела выражаются моментом инерции тела – J.
МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Моментом импульса материальной точки относительно оси вращения называют векторную величину, модуль которой
![]() .
.
![]() (25)
(25)
Тогда момент импульса абсолютно твердого тела относительно неподвижной оси вращения
![]() или в векторной форме
или в векторной форме
![]() ,
(26)
,
(26)
т.е.
![]() лежит на оси вращения и совпадает по
направлению с
лежит на оси вращения и совпадает по
направлению с
![]() (на-
(на-
правление
![]() определяется так же как и для
определяется так же как и для
![]() – по правилу буравчика).
– по правилу буравчика).
Запишем для нашего тела основное уравнение динамики вращательного движения в виде:
![]() (27)
(27)
Если М = 0, то dL/dt = 0 т.е.
L = J = const. (28)
Момент импульса тела остается неизменным, если суммарный момент всех внешних сил действующих на тело равен нулю – это закон сохранения момента импульса.
Для системы из N тел, которые вращаются вокруг общей оси, закон сохранения импульса записывается в виде:
![]() . (29)
. (29)
РАБОТА И ЭНЕРГИЯ ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИИ
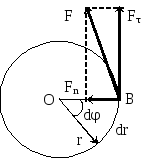 Пусть под действием силы
Пусть под действием силы
![]() ,
приложенной в точке В, тело повернулось
на угол d.
Определим элементарную работу этой
силы. Разложим силу
,
приложенной в точке В, тело повернулось
на угол d.
Определим элементарную работу этой
силы. Разложим силу
![]() на нормальную и тангенциальную
составляющие. Очевидно, что
на нормальную и тангенциальную
составляющие. Очевидно, что
![]() работы не производит, т.к. перпендикулярна
перемещению тела. Тогда
работы не производит, т.к. перпендикулярна
перемещению тела. Тогда
![]() . (30)
. (30)
Работа
при повороте тела из положения
определяющегося углом
![]() в положение
в положение
![]() будет
будет
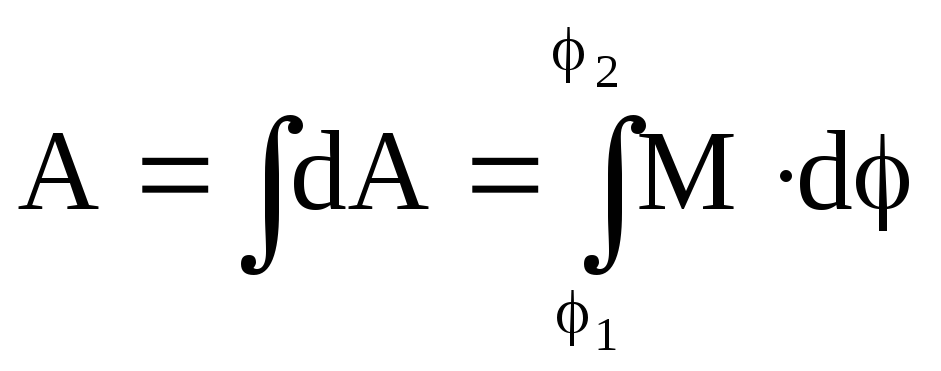 . (31)
. (31)
Кинетическую энергию вращающегося тела можно представить как сумму кинетических энергий бесконечно малых элементов этого тела с массой m и скоростью 1.
![]() . (32)
. (32)
Подставим
![]() и
и
![]() в (30)
в (30)
![]() .
(33)
.
(33)
1.2. Механические колебания. Незатухающие и затухающие колебания. Дифференциальное и кинематическое уравнение затухающих колебаний. Параметры затухания: коэффициент затухания, декремент затухания, логарифмический декремент затухания. Вынужденные колебания. Резонанс. Механические волны. Кинематическое и дифференциальное уравнение волны. Поток энергии волны. Вектор Умова.
Колебаниями называется вид движения физических тел или такие процессы, для которых характерна та или иная степень повторяемости во времени. Например, принципом повторяемости обладают: движения маятника и гитарной струны, голосовых связок и барабанной перепонки уха, колебания температуры воздуха и напряжения в электросети, изменение освещенности на улице в связи со сменой дня и ночи и т.д. Как видно из приведенных примеров, колебания имеют различное происхождение, иначе говоря, разную физическую природу: колебания механические, тепловые, электрические, электромагнитные, оптические и др.
Если повторяемость состояний колеблющейся системы имеет произвольный характер, то такие колебания называются апериодическими или непериодическими. Колебания, для которых последовательность состояний системы повторяется через равные промежутки времени, называются периодическими. В дальнейшем мы будем рассматривать в основном периодические колебания.
В зависимости от характера воздействия, оказываемого на колебательную систему извне, различают: свободные (или собственные) колебания и колебания вынужденные. По этому признаку различают еще автоколебания и параметрические колебания.
Свободными называются колебания, которые совершаются за счет внутренних сил системы, предоставленной самой себе после того, как ей был сообщён внешний первоначальный толчок, породивший эти колебания. Например, шарик на нити.
Вынужденными называются колебания, которые совершаются под постоянным воздействием внешней переменной силы. Например, колебания моста, когда по нему идут пешеходы.
Если с течением времени запас энергии колебательной системы не меняется, то такое колебание называется незатухающим. Если же эта энергия уменьшается, то – затухающим.
Независимо от природы, все виды колебательного движения имеют общие закономерности, т.е. протекают по одним и тем же законам и характеризуются одними и теми же параметрами: периодом Т, частотой ν, амплитудой А и фазой φ.
Закон колебательного движения – это уравнение, которое показывает, как с течением времени изменяются параметры, описывающие состояния колеблющегося тела. Простейшими являются гармонические колебания, для которых изменение величин, описывающих состояние системы, происходит по закону синуса или косинуса. Этот вид колебаний особенно важен, т.к. в природе и в практической сфере колебания очень часто имеют характер близкий к гармоническому или могут быть представлены как сумма нескольких простых гармонических колебаний.
НЕЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Получим закон гармонических колебаний на примере механического движения механических колебаний. Это вид колебаний, при котором тело поочерёдно и многократно совершает отклонения от своего положения равновесия в одну и другую сторону.
Р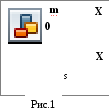 ассмотрим
колебания пружинного маятника вдоль
горизонтальной оси при отсутствии силы
сопротивления. Пружинный маятник
представляет собой массивный шарик
массой m, прикрепленный
к пружине с ничтожно малой массой и
жесткостью k. Другой
конец пружины закреплен неподвижно.
Если вывести шарик из равновесия и
отпустить, то под воздействием силы
упругости деформированной пружины
система пружина–шарик придет в
колебательное движение. Положение
шарика на оси будем определять смещением
s, т.е. расстоянием от
положения равновесия до шарика (рис.1).
Наша цель решить основную задачу
механики – найти ответ на вопрос: где
будет находиться тело в произвольный
момент времени t, т.е.
найти вид функции s = f(t)?
ассмотрим
колебания пружинного маятника вдоль
горизонтальной оси при отсутствии силы
сопротивления. Пружинный маятник
представляет собой массивный шарик
массой m, прикрепленный
к пружине с ничтожно малой массой и
жесткостью k. Другой
конец пружины закреплен неподвижно.
Если вывести шарик из равновесия и
отпустить, то под воздействием силы
упругости деформированной пружины
система пружина–шарик придет в
колебательное движение. Положение
шарика на оси будем определять смещением
s, т.е. расстоянием от
положения равновесия до шарика (рис.1).
Наша цель решить основную задачу
механики – найти ответ на вопрос: где
будет находиться тело в произвольный
момент времени t, т.е.
найти вид функции s = f(t)?
Примем за начало отсчета точку 0, в
которой находится центр шарика в
равновесном состоянии системы, т.е. при
отсутствии деформации в пружине. Пусть
в момент времени t шарик
находится на расстоянии s
от положения равновесия. Характер
движения в данный момент времени
определяется равнодействующей приложенных
к шарику сил:
![]() .
Т.к. трение по условию отсутствует, а
сила тяжести
.
Т.к. трение по условию отсутствует, а
сила тяжести
![]() перпендикулярна стержню, то характер
движения будет определяться только
силой упругости деформированной пружины:
перпендикулярна стержню, то характер
движения будет определяться только
силой упругости деформированной пружины:
![]() (1)
(1)
В соответствии со 2-ым законом Ньютона
эта сила сообщает шарику ускорение
![]() ,
тогда в скалярном виде можно записать:
,
тогда в скалярном виде можно записать:
![]() ,
(2)
,
(2)
но т.к. a = d2s /dt2 то
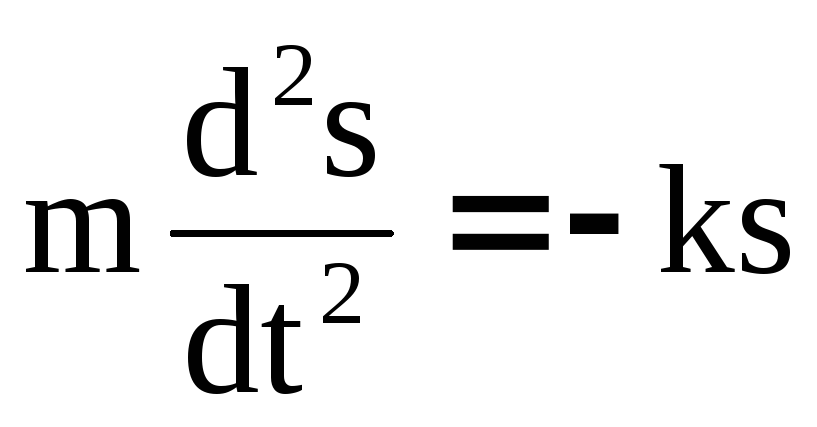 .
(3)
.
(3)
Разделим правую и левую часть (3) на m
и обозначим k/m
=
![]() .
Сгруппировав все члены в левой части
равенства, получим дифференциальное
уравнение гармонических колебаний.
.
Сгруппировав все члены в левой части
равенства, получим дифференциальное
уравнение гармонических колебаний.
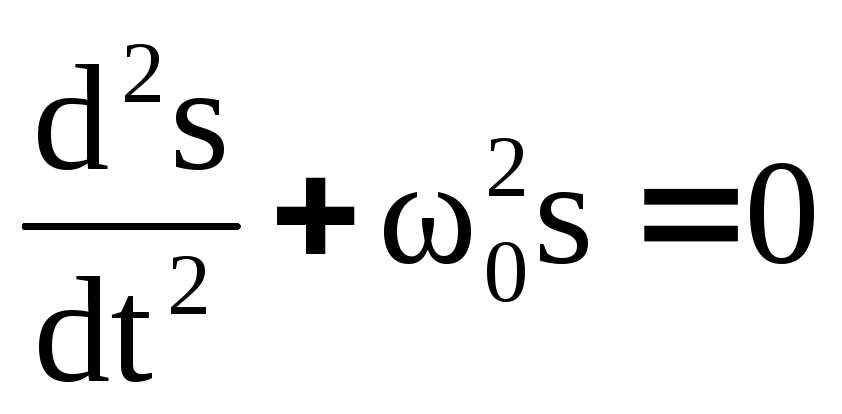 или
или
![]() .
(4)
.
(4)
Это дифференциальное уравнение второго
порядка с постоянными коэффициентами.
Его характеристическое уравнение: к2
+![]() = 0, корни которого к1,2 = ±iω0
– мнимые числа. Тогда общее решение
(4) будет:
= 0, корни которого к1,2 = ±iω0
– мнимые числа. Тогда общее решение
(4) будет:
s = С1cosω0t + C2sinω0t. (5)
Для любых С1 и С2 всегда можно подобрать другие произвольные постоянные А и φ0 такие, что С1 = Аsin φ0 а С2 = Аcosφ0, Тогда общее решение (4) примет вид:
s = А(sin φ0,1·cosω0t + cosφ0,1·sinω0t) = Аsin(ω0t + φ0,1). (6)
Если выражения для С1 и C2 поменять местами (С1 = Аcosφ0 а С2 = Аsin φ0), то общее решение будет иметь вид:
s = А(cos φ0,2·cosω0t + sinφ0,2·sinω0t) = Аcos(ω0t + φ0,2) (7)
Данные функции (6) и (7) и есть искомые
кинематические уравнения гармонического
колебания. Аргумент этой функции (0t
+ φ0) называется фазой колебания;
0 – постоянная
составляющая фазы называется начальной
фазой;
![]() – собственная циклическая (круговая)
частота колебаний данного пружинного
маятника (
– собственная циклическая (круговая)
частота колебаний данного пружинного
маятника (![]() ,
,
![]() ,
тогда
,
тогда
![]() );
А – амплитуда колебаний, в данном случае
максимальное значение смещения s.
В общем случае амплитуда А – это
наибольшее значение величины, изменение
которой с течением времени выбрали для
описания изучаемых колебаний.
);
А – амплитуда колебаний, в данном случае
максимальное значение смещения s.
В общем случае амплитуда А – это
наибольшее значение величины, изменение
которой с течением времени выбрали для
описания изучаемых колебаний.
Графики гармонического колебания представляют собой синусоиды:
П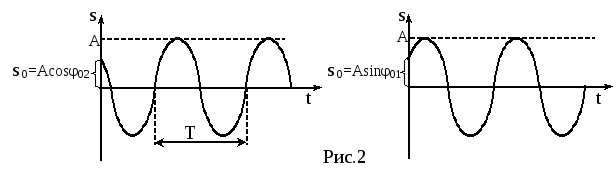 олучим
уравнения, описывающие изменения
скорости и ускорения тела, совершающего
гармонические колебания. Пусть s
= Аcos(ω0t
+ φ0), тогда
олучим
уравнения, описывающие изменения
скорости и ускорения тела, совершающего
гармонические колебания. Пусть s
= Аcos(ω0t
+ φ0), тогда
![]() ,
(8)
,
(8)

![]() .
(9)
.
(9)
Как видно, скорость и ускорение тоже изменяются по гармоническим законам, но скорость опережает по фазе смещение на /2, а ускорение на (рис.3), т.е. ускорение находится в противофазе со смещением. В целом, тела, на которые действуют равнодействующие вида F = -kx (такие силы называются квазиупругими), будут совершать гармонические колебания.
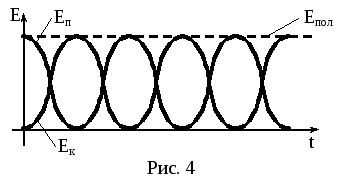
Рассмотрим процесс колебательного движения с энергетической точки зрения. Смещая тело из положения равновесия, мы деформируем пружину, сообщая системе тем самым запас потенциальной энергии. Отпустив тело, мы даем ему возможность двигаться к положению равновесия. При этом потенциальная энергия системы, превращается в кинетическую. В момент прохождения положения равновесия потенциальная энергия полностью превращается в кинетическую. Продолжая движение по инерции, тело опять деформирует пружину, т.е. кинетическая энергия начинает превращаться в потенциальную. В момент, когда кинетическая энергия полностью превратится в потенциальную, смещение достигнет амплитудного значения, тело остановится и начнет двигаться обратно. Опять потенциальная энергия будет превращаться в кинетическую и т.д. (рис4). Т.о., с точки зрения энергетической, механическое колебание – это процесс многократных, последовательных превращений потенциальной энергии в кинетическую и обратно.
![]() (10)
(10)
![]() ,
(11)
,
(11)
![]() ,
(12)
,
(12)
т.е. полная энергия системы величина постоянная.
ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
В реальных условиях, кроме возвращающей силы в колебательной системе обязательно будет действовать и сила сопротивления. Будет считать, что скорости движения при колебаниях будут небольшими, тогда сила сопротивления прямо пропорциональна скорости:
![]() ,
(13)
,
(13)
где r –коэффициент сопротивления. Учитывая только силу сопротивления (13) и силу упругости (1) согласно II закону Ньютона для уравнения движения получим:
![]() (14)
(14)
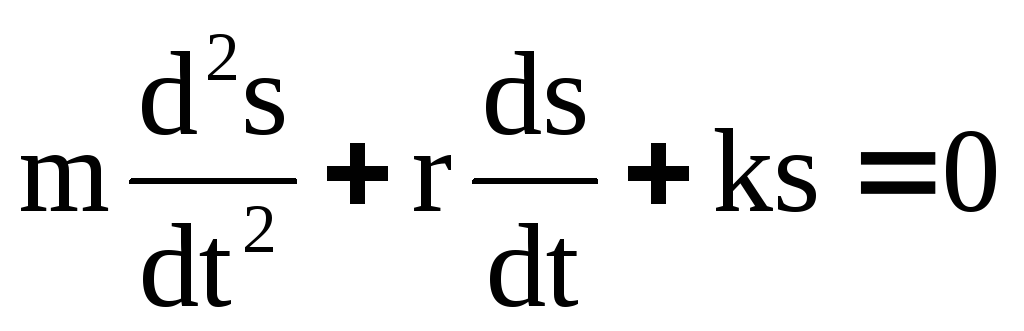 (15)
(15)
Разделив правую и левую часть (15) на m
и обозначив k/m
=
![]() ,
а r/m = 2β,
получим:
,
а r/m = 2β,
получим:
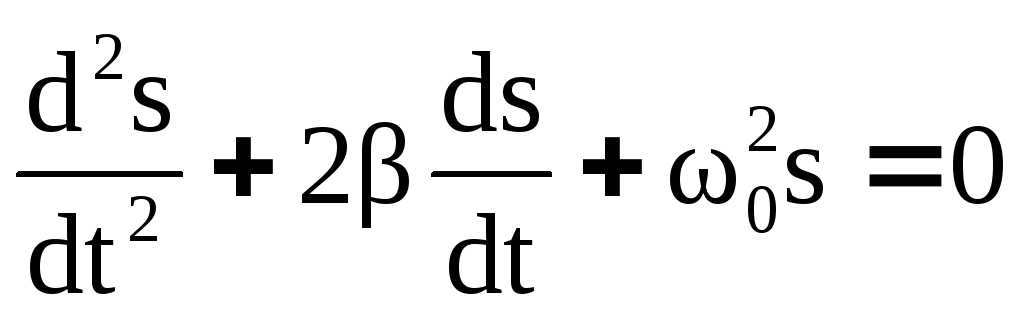 или
или
![]() (16).
(16).
