9.Застосування визначеного інтеграла до знаходження площі фігури та об’єму тіла обертання

Формула Ньютона – Лейбніца

1.Нехай на інтервалі [a, b] задана неперервна невідємна функція у=f(x). Тоді згідно з геометричним змістом визначеного інтеграла площа криволінійної трапеції, обмеженої даною функцією, віссю ОХ та прямими х=а, х=b, чисельно дорівнює визначеному інтегралу.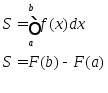

Знаходження об`ємів фігур обертання

12. Диференціальні рівняння зі сталими коефіцієнтами. Теореми про структуру розвязків о.Л. Д.Р і н.Л.Д.Р.

Лінійне диференційне рівняння зі сталими коефіцієнтами з правою частиною спеціального виду - диференційне рівняння виду

,

де коефіцієнти - певні сталі, - довільна функція.

Однорідне лінійне диференційне рівняння зі сталими коефіцієнтами

14. Ознаки збіжності додатніх рядів

Сформулюємо дві ознаки збіжності додатніх рядів, що ґрунтуються на порівнянні рядів між собою. Ці ознаки полягають в порівнянні членів досліджуваного ряду з членами іншого ряду, поведінка якого вже вияснена.

1. Нехай 1)

І 2)

- два додатніх ряди, причому члени першого, починаючи з деякого місця, не більші відповідних членів другого:. Тоді, якщо ряд (2) збігається, то збігається і ряд (1), якщо ж ряд (1) розбігається, то розбігається і ряд (2) ( із збіжності ряду з більшими членами випливає збіжність ряду з меншими членами, із розбіжності ряду з меншими членами випливає розбіжність ряду з більшими членами).

2. Якщо ряди (1) і (2) строго додатні і границя відношення їх загальних членів є обмежене додатнє числото ряди (1) і (2) збігаються або розбігаються одночасно.

В багатьох випадках для порівняння досліджуваного ряду зручно використовувати ряди видуМи будемо називати такі ряди гармонійними, хоч частіше цю назву відносять лише до рядуПізніше ми розглянемо ознаки збіжності, з допомогою яких можна буде показати, що гармонійні ряди збігаються при>1 і розбігаються при 0<≤1

Розглянемо декілька прикладів.

Приклад 1. При всіхочевидна нерівність<Оскільки ряд з більшими членамизбігається, то за ознакою 1 збігається і розглядуваний ряд.

(ознака Даламбера). Якщо для рядуз додатними членамиіснує границя тоді:

приряд збігається;

приряд розбігається;

при питання про збіжність ряду ознака не вирішує.

15. Знакозмінні ряди. Абсолютна та умовна збіжність. Теорема Лейбніца

Теорема. Якщо в ряді з додатними членами загальний член, починаючи з певного значення п, задовольняє нерівність деq – стале число, менше за одиницю, то ряд збігається.

Коли ж навпаки, починаючи з певного значення п, маємо то ряд розбігається.

Наслідок. Якщо існує , то приr < 1 ряд напевне збігається. Випадок r = 1 і тут взагалі є сумнівний.

Теорема. Ряди напевне збігається, якщо збігається ряд

Означення. Збіжний ряд називається абсолютно збіжним. Якщо збігається також і ряд

Означення. Якщо ряд (*) збіжний, а рядрозбіжний, то даний ряд (*) називається умовно збіжним.

Означення. Знакозмінними рядами називаються ряди виду:

де - додатні числа.

Теорема Лейбніца. Якщо в знакозмінному ряді абсолютне значення загального члена монотонно прямує до нуля (тобто до того ж), тоді знакозмінний ряд збігається, причому сума його має числове значення, проміжне між нулем та першим членом

16. Степеневі ряди. Теорема Абеля. степеневим рядом називається нескінченний ряд виду:  де a_n — коефіцієнти n - го доданку, c — деяка константа, а x — змінна визначена в деякій області, що містить c. На практиці часто c рівне нулю і степеневі ряди мають простіший вид:

• Перша теорема Абеля: якщо степеневий ряд є розбіжним при , він є розбіжним при всіх 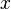, таких що .

Друга теорема Абеля: Нехай степеневий ряд є збіжним в точці . Тоді він є рівномірно збіжним пона відрізку, що сполучає точки 0 і.

-Степеневий ряд називається збіжним в точці x₀, якщо збіжним  є відповідний числовийряд 

Степеневий ряд є збіжним в деякій області, якщо він є збіжним в кожній точці цієї області.