1. Невизначений інтеграл та його властивості.

Означення. Якщо F(x) – первісна f(x), x є І, то вираз F(x)+с, де с – будь-яке число називається невизначеним інтегралом функції f(x) (або виразу f(x)dx) і записується .

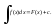Вираз 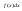називається підінтегральним виразом,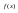називається підінтегральною функцією.

Приклад.

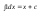
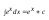
Властивості невизначених інтегралів

1. 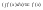- операція інтегрування і взяття похідної взаємно обернені.

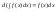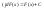2. і, значки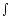іd взаємно скорочуються .

3. .

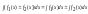4. .

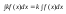5. Оскільки формула для диференціалу 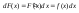інваріантна відносно х і значки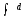взаємно скорочуються то, взявши з обох боків інтеграли отримаємо, що формула для інтеграла має таку ж властивість, тобто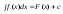правильна і тоді коли х є внутрішня функція, тобто

, .

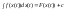
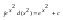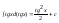2. Основні методі знаходження невизначеного інтегралу. Метод безпосереднього інтегрування

Цей метод базується на рівності сталі і застосовується у тих випадках, коли підінтегрільна функціяf має вигляд однієї із підінтегральних функцій таб­личних інтегралів, але її аргумент відрізняється від змінної інтегрування постійном доданком або постійним множником або постійним множником та постійним доданком.

Метод підстановки (заміни змінної)

Цей метод містить два прийоми.

a) Якщо для знаходження заданого інтеграла ∫f(x)dx зробити підстановку x = φ(t), тоді має місце рівність

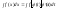
Після знаходження останнього інтеграла треба повернутись до початкової змінної інтегрування х. Для застосування цього прийому треба; щоб функція х - φ (t) мала обернену t = ψ(х)

b) Якщо зробити заміну змінної, тобто t = φ (х) тоді має місце

рівність

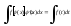
Після знаходження останнього інтеграли треба повернутись до змінної х, використовуючи рівність t = φ (х).

Метод інтегрування частинами

Цей метод застосовується тоді, коли під інтегралом є добуток функцій, причому хоча би одна з них є трансцендентною (не степеневою).

Нехай u та v деякі функції х, тобто u = u(x), v = v(x).

Розглянемо диференціал добутку цих функцій.

d(uv) = udv + vdu

Інтегруючи обидві частини рівності, одержимо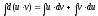

Звідси, враховуючи властивість не визнач. інтеграла, маємо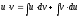

Отже, одержали формулу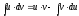,яку називають формулою інтегрування частинами.

Ця формула дозволяє знаходження інтеграла 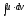звести до зна­ходження інтеграла. При вдалому обранніu то dv інтеграл може бути табличним або простішим ніж заданий інтеграл

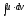
3. Інтегрування раціональних ф-ій

Означення: Раціональний дріб правильний, якщо степінь многочлена в чисельнику менший степеня многочлена в знаменнику, тобто n<m. Якщо ж n³m, то дріб неправильний. Методика інтегрування раціональних ф-ій: 1. Якщо підінтегральна ф-ія – неправильний раціональний дріб, то за допомогою ділення його розкладають на суму многочлена і правильного раціонального дробу. 2. Знаменник правильного раціон. дробу розкладають на множники. По вигляду знаменника, правильний раціон. дріб представляють у вигляді найпростіших дробів, використовуючи метод невизначених коефіцієнтів. 3. Інтегрують цілу частину і найпростіші дроби. 4. Інтегрування тригонометричних функцій 

Інтегрування функцій вигляду R(sin x, cos x) зводиться до інтегрування раціональних функцій за допомогою універсальної тригонометричної підстановки tg(x/2) = t. Тоді sin x =--2; cos x =-T; x = 2 arctg t; dx = —2. 1 +12 1 +t2 1 +12dx В деяких випадках знаходження інтегралів j R (sin x ■ cos x) ds значно спрощується підстановками: 1) якщо функція R(sinx, cosx) непарна щодо sinx — підстановкою cosx = t, 2) якщо функція R(sinx, cosx) непарна щодо cosx — підстановкою sinx = t, 3) якщо функція R(sinx, cosx) парна щодо sinx і cosx — підстановкою tgx = tdx При знаходженні j sinm xcosn xdx можливі випадки: 1) m — непарне додатне число — підстановка cos x = t, n — непарне додатне число — підстановка sin x = t, 2) m і n — парні додатні числа — підінтегральна функція перетворюється за допомогою формул зниження степеня.

№5 Визначений інтеграл його властивості та геометричний зміст.

Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервнимфункціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — цевідрізок числової осі.

Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссюабсцис, двома вертикалями на краях відрізка і кривою графіка функції.

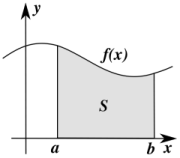Визначений інтеграл дорівнює площікриволінійної трапеції, обмеженої кривою. Властивості: 1.Величина визначеного інтеграла не залежить від позначення змінної інтегрування:

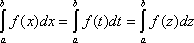тощо. Інтегральна сума, а отже, і її границя не залежать від того, якою буквою позначено аргумент функції f. Це й означає, що визначений інтеграл не залежить від позначення змінної інтегрування.Визначений інтеграл введений для випадку, коли ab.

2. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю:

3. Від переставлення меж інтегрування інтеграл змінює знак на протилежний:

№6 основні методи інтегрування визначеного інтегралу

1.Метод підстановки (заміни змінної) 

Цей метод містить два прийоми.

a) Якщо для знаходження заданого інтеграла ∫f(x)dx зробити підстановку x = φ(t), тоді має місце рівність: 

Після знаходження останнього інтеграла треба повернутись до початкової змінної інтегрування х. Для застосування цього прийому треба, щоб функція х - φ (t) мала обернену t = ψ(х).

b) Якщо зробити заміну змінної, тобто t = φ (х) тоді має місце рівність: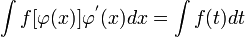 

Після знаходження останнього інтеграла треба повернутись до змінної х, використовуючи рівність t = φ (х)

2. Метод інтегрування частинами 

Цей метод застосовується тоді, коли під інтегралом є добуток функцій, причому хоча би одна з них є трансцендентною (не степеневою).

7. Наближені методи обчислення визначеного інтегралу Багато задач науки і техніки приводять до проблеми обчислення інтегралів, але не всі інтеграли піддаються обчисленню. разглядається питання наближеного обчислення визначених інтегралів, що не беруться через елементарні функції. Зокрема, виводяться формули наближеного обчислення прямокутників, формула трапецій а також формула Сімпсона. Формули прямокутників і трапеції. Нехай треба обчислити значення визначеного інтегралу 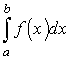де є деяка задана на проміжку неперервна функція. Існує багато прикладів обчислення подібних інтегралів, або за допомогою первістної, якщо вона виражається в скінченному вигляді. Потрібно відмітити, однак, що всім цим вичерпується вузький клас інтегралів; за його межами зазвичай вдаються до різних методів наближеного обчислення. Перші формули, які сюди відносяться, простіші всього отримуються із геометричних міркувань. Витлумачуючи визначений інтеграл як площу деякої фігури, яка обмежена кривою , ми і ставимо перед собою задачу знаходження цієї площі. Перш за все, вдруге використовуючи ту думку, яка привела нас до самого поняття о визначеному інтегралі, можна розбити усю фігуру на смуги, скажемо однієї і той же ширини , а потім кожну смугу наближено замінити прямокутником, за висоту якого прийнята будь-яка із його ординат. Це приводе нас до формули

,де .Тут шукана площа криволінійної фігури замінюється площею деякої ступенчатої фігури, яка складається із прямокутників (або ж, можно сказати, що визначений інтеграл замінюється інтегральною сумою). Ця наближена формула і називається формулою прямокутників. Геометричні міркування природньо приводять і до другої, часто використовуваємій наближеній формулі. Замінивши дану криву вписаною в неї ламаною, з вершинами у точках , где . Тоді наша криволінійна фігура заміниться іншою, яка складається із ряду трапецій (рис2.). Якщо, як і раніш рахувати, що проміжок разбитий на рівні частини, то площі цих трапецій будуть

Додаючи, прийдемо до нової наближеної формули

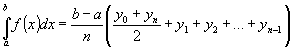. (2) Це так звана формула трапецій. Також можемо прийти до формули

 Вона носит назву формули Сімпсона (Th. Simpson); цією формулою користуються для наближенного обчислення інтегралів частіші, аніж формулами прямокутников і трапецій, бо она – при тих же затратах – дає зазвичай більш точний результат.

8. Невластиві інтеграли Вводячи поняття інтегралу, ми припускали, що відрізок інтегрування кінцевий, а подінтегральна функція обмежена на цьому відрізку. В протилежному випадку множина сум Дорту не буде обмеженою. Але можливі випадки коли одна або дві ці умови не виконуються. В такому випадку відповідні інтеграли називаються невластивими.

1-го роду. Границя інтегралу 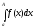(кінцева або нескінченна) приА  +  називається невластивим інтегралом І-го роду від функції f(x).

Позначення.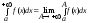

2-го роду. Нехай функція у = f(x) визначена на проміжку (a; b].

Означення: Точка х = b називається особливою точкою якщо функція f(x) не обмежена в будь-якому відрізку, що належать проміжку (a; b].

Теорема. Якщо існує границя

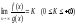
то із збіжності інте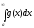грала , приK < + випливає збіжність інтеграла 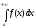, а із розбіжності першого інтеграла впливає розбіжність другого.

Теорема: Нехай для достатньо великих х (Коші) функція f(x) має вид

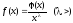
Тоді: 1) якщо  > 1 і (х)  с > 0, то цей інтеграл розбігається.

Теорема: Якщо збігається інтеграл 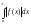то збігається і інтеграла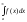

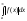Означення: Якщо одночасно з інтегралом збігається інтеграл, то інтегралназиваєтьсяабсолютно збіжним, а функція f(x) — абсолютно інтегровною на проміжку [a; b).

Теорема: Нехай функція f(x) і g(x) визначені на проміжку [a; ) причому:

1) функція f(x) інтегровна на цьому проміжку так що інтеграл (1) збігається;

2) функція g(x) монотонна і обмежена:

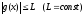
Тоді інтеграл 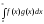збігається.

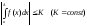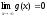Теорема Ознака Діріхла: Нехай 1) функція f(x) інтегровна на будь-якому проміжку [а; А] і інтеграл (7) обмежений: 2) функція g(x) монотонно прямує до 0 при х  : . Тоді інтеграл збігається.